跳不出“长方体”掌心的“三棱锥”

方汪涛

(湖南省岳阳市岳阳中学 414000)

三棱锥是常见的最简单的几何体，也是高考对几何体考查常常青睐的背景对象. 许多三棱锥问题直接解决比较困难，但如果将三棱锥还原成一个长方体，问题往往就迎刃而解.

一、棱长都相等的三棱锥↔正方体

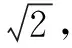
图1 图2

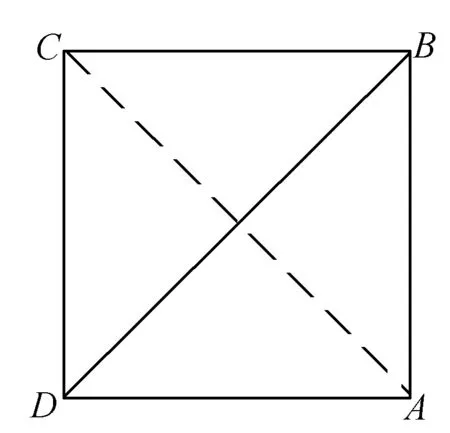
图3

解析此题情境设置简洁，解决方法也多，通常可以考虑作出对棱的公垂线段再转化为直角三角形求解. 不过若能意识到把这个正四面体置于一个正方体结构中(如图2)，则瞬间得到结果，所求距离就是该正方体的棱长，为1，选A.

点评正四面体的可以通过正方体切割得到，当然正四面体也可以还原为正方体. 正四面体的六条棱就是这个还原正方体的六条面对角线.从而它们之间的关系显而易见. 同学们试试这个问题：已知正四面体的俯视图如图3所示，其中四边形ABCD是边长为2的正方形，则这个正四面体的体积为 .

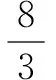
二、共点的棱两两垂直的三棱锥↔长方体

图4

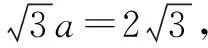
点评这是2012年高考辽宁理科试题，以侧棱两两垂直的正三棱锥为背景，考查与球的关系. 如果直接从正三棱锥入手，则比较困难. 抓住侧棱两两垂直，即教室的墙角，可以还原为正方体整体解决.

三、不共点的棱互相垂直的三棱锥↔长方体

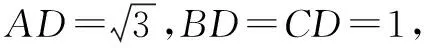
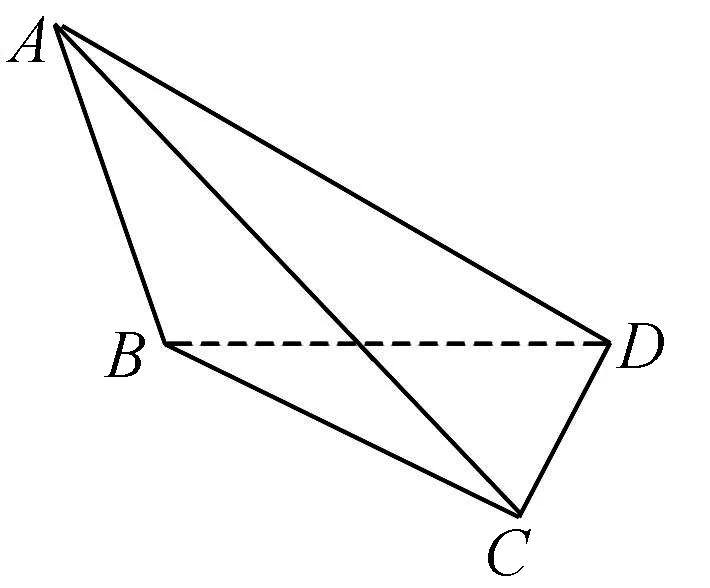
图5

(1)求证：AD⊥BC；

(2)求二面角B-AC-D的余弦值；

(3)在线段AC上是否存在一点E，使ED与平面BCD成30°角？若存在，确定点E的位置；若不存在，说明理由.

解析(1)作AH⊥平面BCD于H，连接BH,CH,DH，则四边形BHCD是正方形，且AH=1.以D为原点，DB所在直线为x轴，DC所在直线为y轴，建立如图6所示的空间直角坐标系，则B(1,0,0),C(0,1,0),A(1,1,1)，

图6

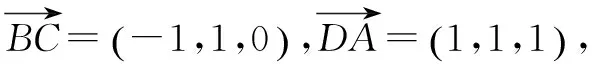
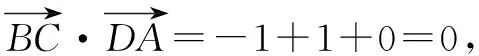
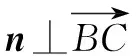
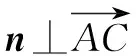
同理可求得平面ACD的一个法向量为m=(1,0,-1).

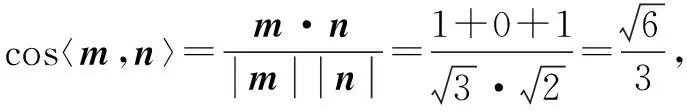
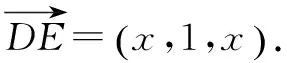
故线段AC上存在一点E，使ED与平面BCD成30°角，且当CE=1时，ED与平面BCD成30°角.

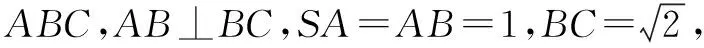
A.4π B.3π C.2π D.π

答案A.

四、对棱相等的三棱锥↔长方体

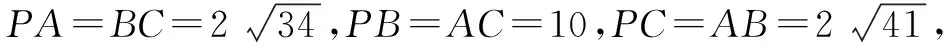
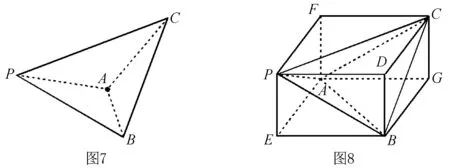
解析如图8所示，把三棱锥P-ABC补成一个长方体AEBG-FPBG，易知三棱锥P-ABC的各边分别是长方体的面对角线.

不妨令PE=x,EB=y,EA=z，则由已知有

从而知VP-ABC=VAEBG-FPDC-VP-AEB-VC-ABG-VB-PDC-VA-FPC

故所求三棱锥P-ABC的体积为160.

点评三对对棱相等的三棱锥，可以还原为长方体，使得对棱是长方体相对面的面对角线. 从而利用长方体的关系解决有三对对棱相等的三棱锥问题. 同学们试试这个问题：在四面体ABCD中，AB=CD=6,AC=BD=4,AD=BC=5，则四面体ABCD的外接球的表面积为 .

怎么样？三棱锥再怎么调皮变化，也无法跳出“长方体”的掌心.所以以后同学们遇到三棱锥问题，就直接还原找长方体吧.

参考文献：

[1]赵临龙.圆内接四边形面积最值的理论研究[J].河南科学,2011(6).