中点问题解题策略

于长江

(黑龙江省克山县第二中学校 161600)

添加辅助线解几何命题,是学习平面几何的难点;作辅助线虽无定法,但却有规可循,有律可导，只要深刻挖掘题设与结论的内含，抓住特定条件的本质特征，探求已知与未知之间的必然联系，灵活运用所学知识，增强创新意识，定能架起沟通已知与未知之间的桥梁——辅助线.通过引辅助线，可以转化条件，制造联系，从而达到解决问题的目的.现举例如下.

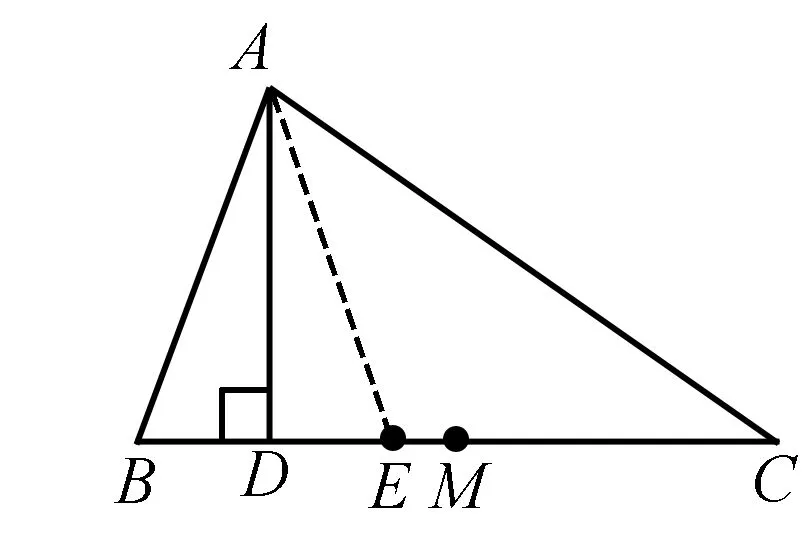
如图，在△ABC中，AD是高，M是BC中点，∠B=2∠C，

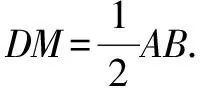
分析本题的特定条件有中点(M点)、2倍角(∠B=2∠C)、高线(AD)，在解题时以某一条件为出发点，根据其不同特性引辅助线，得出以下多种解题方法.

一、构造中位线法

当条件中出现中点时，一般可取另一边的中点，构造中位线，制造平行关系或等量关系.

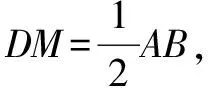
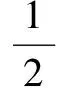
∴∠2=∠C.而∠1=∠2+∠3，∠B=2∠C，

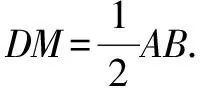
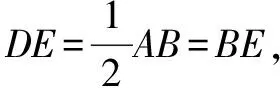
∴∠B=∠1.而∠1=∠2+∠3，∠B=2∠C，

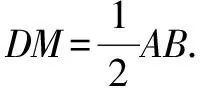
二、中线加倍法

当条件中出现三角形的中线或可作中线时，可考虑将中线延长一倍，构造全等三角形，转化条件.

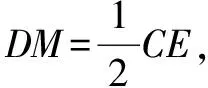
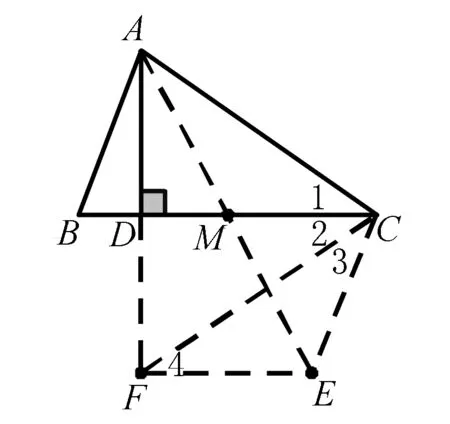
证法3 连AM并延长到E，使ME=AM，

连CE,延长AD到F，使DF=AD，连EF、CF.

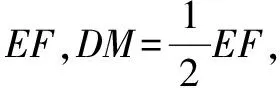
易证△AMB≌△EMC，

∴CE=AB，∠B=∠2+∠3.

由BC垂直平分AF得∠1=∠2.而∠B=2∠1，

可得∠2=∠3，∴∠3=∠4，

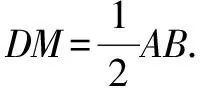
三、2倍角转化法

当条件中出现一个角是另一个角的2倍时，可考虑平分2倍角，或将较小的角加倍.

证法4 延长CB到E，使BE=AB，连AE.

易证∠ABC=2∠E，而∠ABC=2∠C，

∴∠E=∠C，∴AE=AC.而AD⊥EC，

∴DE=CD.在线段EC上可得CE=2CD，

∴BC+EB=2(DM+CM),

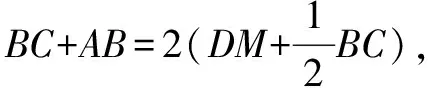
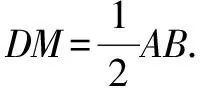
四、高线对称法

将某个三角形沿高线翻折，将构成等腰三角形，从而达到沟通相关条件的目的.

证法5 在DC上截取DE=DB，连AE.

易证△ADE≌△ADB，则AE=AB，

∠AEB=∠B.由∠B=2∠C得∠AEB=2∠C.

而∠AEB=∠CAE+∠C，

∴∠CAE=∠C,∴AE=CE=AB.

在线段BC上可得：BE=2DE，

∴BM+ME=2(DM+ME),

∴CM+ME=2(DM+ME),

∴(AB+ME)+ME=2(DM+ME).

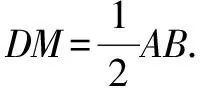
以上五种解法，论述了在特定条件下如何作辅助线及解题策略，以期起到抛砖引玉的作用.

参考文献：

[1]刘义勋. 辅助线是几何证明的“点睛”之笔[J].中学生数学(初中版), 2011(9): 3.