初中生对无理数概念理解的调查与研究

张 硕,张雪妮,2

(1．河北师范大学 数学与信息科学学院 050024； 2.河北省抚宁第二中学 066300)

一、问题的提出

我国《全日制义务教育数学课程标准(2011年版)》指出：了解无理数与实数的概念并能用有理数估计一个无理数的大致范围．我国香港地区中学数学课程标准指出：体验有理数与无理数，发展利用数来构想及解决问题的各种策略．美国中学数学课程标准中指出：在初中阶段安排学生学习有理数，无理数，实数等知识．英国中学数学课程标准指出：中学生需要理解并使用实数中的有理数与无理数并能确定区间边界．日本中学数学课程标准中指出：在数的有关概念的教学中要重视数的意义及大小，并通过数轴来表示数来说明数之间的大小．荷兰中学数学课程标准指出：学生需学会估算，包括与小数和分数有关的估算，并能对估算结果的准确性做出判断，而且可以将分数转化为小数．通过以上各国中学数学课程标准对无理数的提出，可看出无理数在世界各国中学数学中都占有很重要的位置．

但是，据笔者对中学老师的一些访谈及侧面对学生的了解，发现许多学生认为无理数比有理数难懂，对无理数的相关概念，性质等学得一塌糊涂，有些学生甚至不知道无理数是什么，对于有理数的区别也模模糊糊．许多教师认为无理数比较抽象，虽是初中数学的难点，但因中考所占比例不大，因此对这块内容不够重视，也不作更深讲解．笔者还发现一部分教师对无理数发展史也不清楚，虽然教材把无理数编制了一整节内容，但还是不能引起学生及教师的关注．因此笔者认为有必要对学生无理数知识的学习情况进行调查研究．

二、研究过程

2.研究对象

笔者选取了河北省石家庄市的几所不同层次学校的部分九年级学生进行了预调查，并通过整理分析，最终选取河北省石家庄市第二十二中这所普通中学的九年级不同层次的四个班级132名学生作为本研究的测试样本，其中重点班学生共为61人，普通班学生共为71人．

3.研究工具

本文研究使用的测验工具为预测卷、正式测试卷、访谈提纲．

3.统计方法

本研究实际回收试卷132 份，实际有效卷为127份．试卷中所有试题均为主观题目，且均不记分，对问题结果进行水平划分或对学生回答情况进行归类统计．为了根据学生的回答比较学生对无理数概念的掌握情况，笔者借鉴了比格斯的SOLO分类系统将学生对第一题和第二题进行水平的编码划分，具体划分标准说明如下：

水平1：相当于SOLO分类系统的前结构水平．

这一结构水平的学生的回答基本上无法理解无理数的本质特征．

水平2：相当于SOLO分类系统的单一结构水平．

这一结构水平的学生在回答无理数的定义时只找到了无理数的某一类型或者只提及到无理数概念的某一个侧面或举例说明就此结束回答．

水平3：相当于SOLO分类系统的多元结构水平．

这一结构水平的学生在回答无理数的定义时找到了可以代表无理数的多种不同的表现形式，但却未能把这些不同形式有机严谨地整合在一起．

水平4：相当于SOLO分类系统的关联结构水平．

这一结构水平的学生在回答无理数定义时找到了多个无理数概念的表现形式或者知识点，并且能够把这些知识点串联起来．

水平5：相当于SOLO分类系统的抽象拓展结构水平．

这一结构水平的学生回答无理数定义时能够将无理数的概念进行多种不同表述的抽象概括，并且表述逻辑严密，思路清晰，涵盖了所有的知识点．

三、研究结果及分析

问卷中的第一题是让学生写出自己所理解的无理数的概念，并要求学生尽可能多的写出不同的表达方式，第二题是让学生从众多数中选出无理数，目的是要考察学生是否真正掌握了无理数概念的本质．答卷中学生的回答呈现出不同的水平，笔者借鉴了SOLO分类系统进行水平划分(具体划分标准见研究过程中的统计方法)，表1反映了学生对无理数概念的回答水平分布情况．

表1学生对无理数概念的回答水平分类统计表

从上表数据可以看出学生对无理数概念的回答情况绝大部分处于水平3(多元结构水平)共有80人，占全部被试人数的62.9%；处于水平1(前结构水平)、水平2(单一结构水平)、水平4 (关联结构水平)的学生人数相对较少，所占被试人数的比例分别为15.0%，15.0%，5.5%；而处于水平5(抽象结构水平)的学生水平人数更是寥寥无几，仅占所有被试人数的1.6%．其中重点班的学生对无理数概念的掌握情况相对普通班学生对无理数概念的掌握情况要好一些，但差距不是很大．

笔者在统计中发现很多学生出现了同样的几种典型错误并做了如下整理:

典型错误一：不知道π、e也是无理数．

典型错误五：认为无理数只包含小数中的无限不循环小数、开方开不尽的数、以及用特殊符号表示的π、e中的其中一种或两种．

为了更加了解学生发生错误的原因，笔者对个别学生进行了采访，下面为一段访谈记录(T表示笔者，S1表示学生1，S2表示学生2)，由于有些学生表达不是很清楚，因此对一些回答笔者做了一定的逻辑整理．

T:你认为无理数包括哪几种表现形式？

S1：带根号的、除不尽的两个数的商、无法开出来的平方根．

S2：开方开不尽的、带π的数、无限不循环的小数．

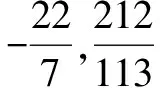
S1：他们都除不尽，应该是无理数．

S2：他们是分数应该是有理数，但他们又除不尽好像又是无限不循环小数是无理数，这样的话不太清楚．

由以上问卷测试和访谈结果可发现绝大多数学生对无理数概念的把握处于不完全理解的状态，他们大多数表现为能够正确地表达出无理数的定义，却对无理数的几种表现形式不清楚，没有掌握无理数的本质.还有些同学不明白分数除不尽的小数是无限循环的并不属于无理数，因此在题二中选择无理数时出现各种各样的错误．

五、教学建议

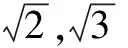
参考文献：

[1]中华人民共和国教育部．全日制义务教育数学课程标准(修订稿)[M]．北京：北京师范大学出版社，2011.

[2]杨秀娟.初中生对无理数概念的理解[D].上海：华东师范大学，2007:1.