利用数学模型探求“线段最值”

卜平平

(江苏省连云港市灌南实验中学 222500)

一、重点知识与命题特点

最值连续多年广泛出现于中考试题中，由冷点变为热点,求相关线段、线段之和差、面积等最大与最小值.此类问题涉及的知识要点有以下方面: ①两点间线段最短；②垂线段最短；③三角形的三边关系；④ 定圆中的所有弦中，直径最长；⑤圆外一点与圆的最近点、最远点.⑥借助转化为代数思想：一次函数反比例函数增减性、二次函数的最值问题.命题特点侧重于在动态环境下对多个知识点的综合考查.

二、真题赏析

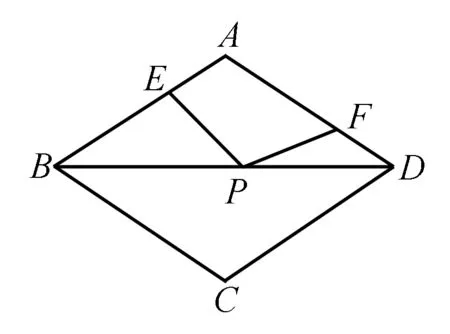
例1 (福建龙岩)如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为( ).

A．1 B．2 C.3 D．4

题型特征利用轴对称求最短路线问题

示范解读此类利用轴对称求最短路线问题一般都以轴对称图形为题设背景,如圆、正方形、菱形、等腰梯形、平面直角坐标系等.首先根据题意画出草图，利用轴对称性找出对应线段之间的相等关系，从而把所求线段进行转化，画出取最小值时特殊位置.两条动线段的和的最小值问题，常见的是典型的是“小河”问题，关键是指出一条对称轴“河流”(如图1)．三条动线段的和的最小值问题，常见的是典型的“牛喝水”问题关键是指出两条对称轴“反射镜面”(如图2)，结合其他相关知识加以解决.

图1 图2

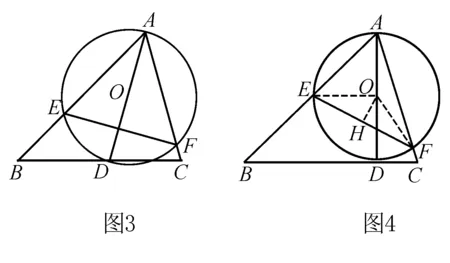
示范解读⊙O的大小随着AD的变化而变化,在此变化过程中,圆周角∠BAC的度数始终保持不变,而线段EF即为⊙O中60°圆周角所对的弦,弦EF的大小随⊙O直径变化的变化而变化,当圆O的直径最小时，60度圆心角所对的弦长最短，即转化为求AD的最小值,由垂线段最短得出当AD⊥BC时,AD最短，如图4.

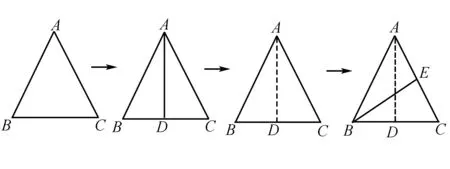
例3 (2017徐州)如图，将边长为6的正三角形纸片ABC按如下顺序进行两次折叠，展开后，得折痕AD,BE(如图1)，点O为其交点.(1)探求AO与OD的数量关系，并说明理由；(2)如图2，若P,N分别为BE,BC上的动点,①当PN+PD的长度取得最小值时，求BP的长度；②如图3，若点Q在线段BO=1上，则QN+NP+PD的最小值= .

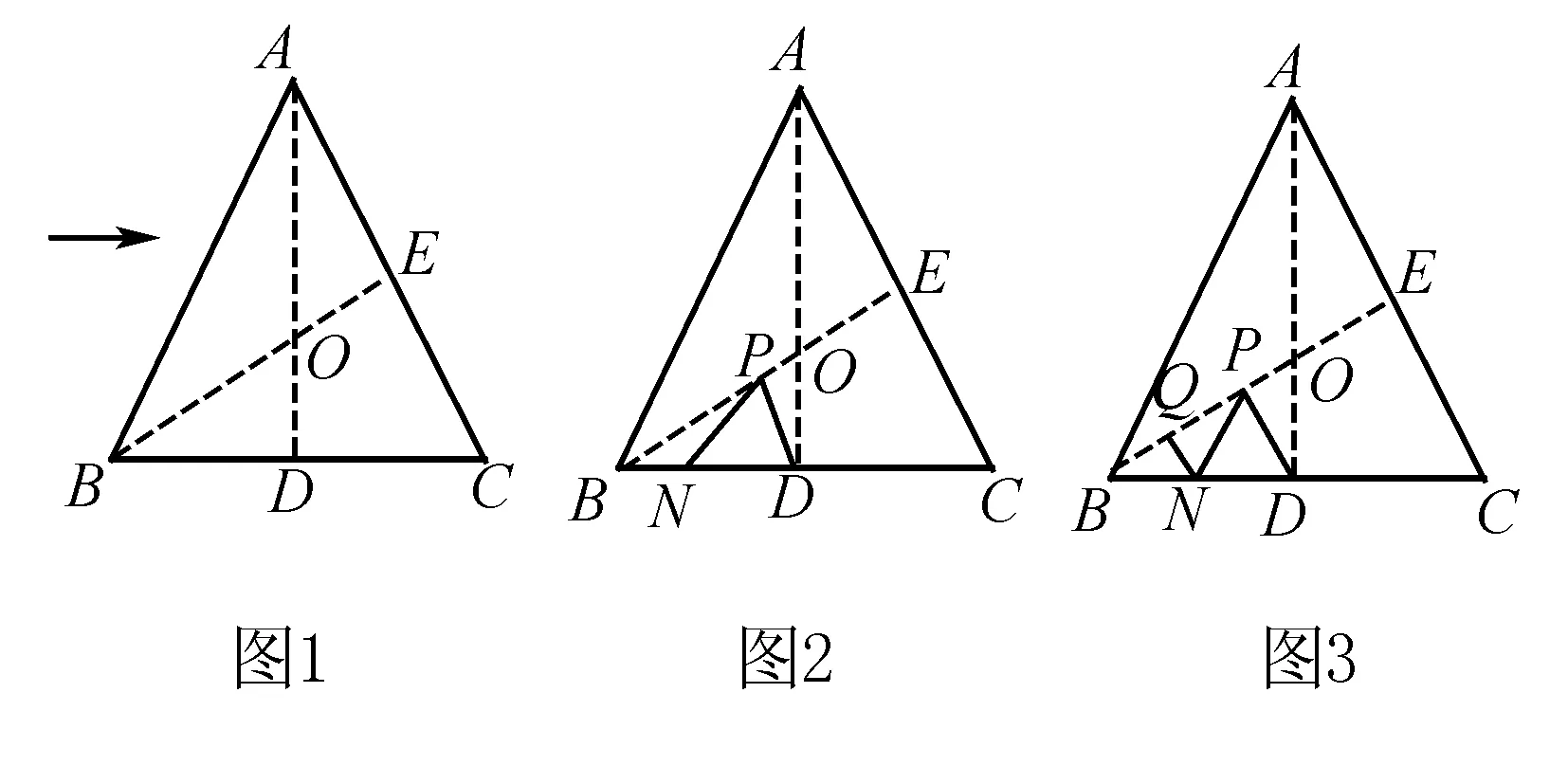
示范解读试题分析：(1)根据等边三角形的性质得到∠BAO=∠ABO=∠OBD=30°,得到AO=OB.根据直角三角形的性质中得到结论.

(3)如图3，作Q关于BC的对称点Q′,作D关于BE的对称点D′,连接Q′D′，即为QN+NP+PD的最小值.根据轴对称的定义得到∠Q′BN=∠QBN=30°,∠QBQ′=60°,得到△BQQ′为等边三角形，△BDD′为等边三角形，解直角三角形即可得到结论.

三、专题总结

几何中的最值问题是指在一定的条件下，求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值，求几何最值问题的基本方法有：1．特殊位置与极端位置法；2．几何定理(公理)法；3．数形结合法等．复习时既要注重对基本知识源的理解与建构，更要注重对相关知识源的综合与整合.在解决本类题型时我们要学会动中觅静，即要分析总结图形中动点在运动过程中不变元素，探寻那些隐含的、在运动变化中的不变量或不变关系．通过不变关系建立相关模型实现最值的转化.

参考文献：

[1]韩兵. 高中数学解题教学中分类讨论思想的培养[J]. 数学大世界(下旬),2016(2):56.

[2] 章建跃.数学学习论与学习指导[M]. 北京：人民教育出版社, 2001.