迭代法求解数学模型的极值问题——如何使正方体容积最大

王一帆 刘小伟

(山东省青岛市第二实验初级中学七年级(11)班 266000)

迭代法是用计算机解决问题的一种基本方法.它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令进行重复执行，在每次执行这组指令时，都从变量的原值推出它的一个新值.迭代是数值分析中通过从一个初始估计出发寻找一系列近似解来解决问题(一般是解方程)的过程，为实现这一过程所使用的方法统称为迭代法.本文利用迭代法解决了含有两个变量的极值求解问题.

一、模型的建立

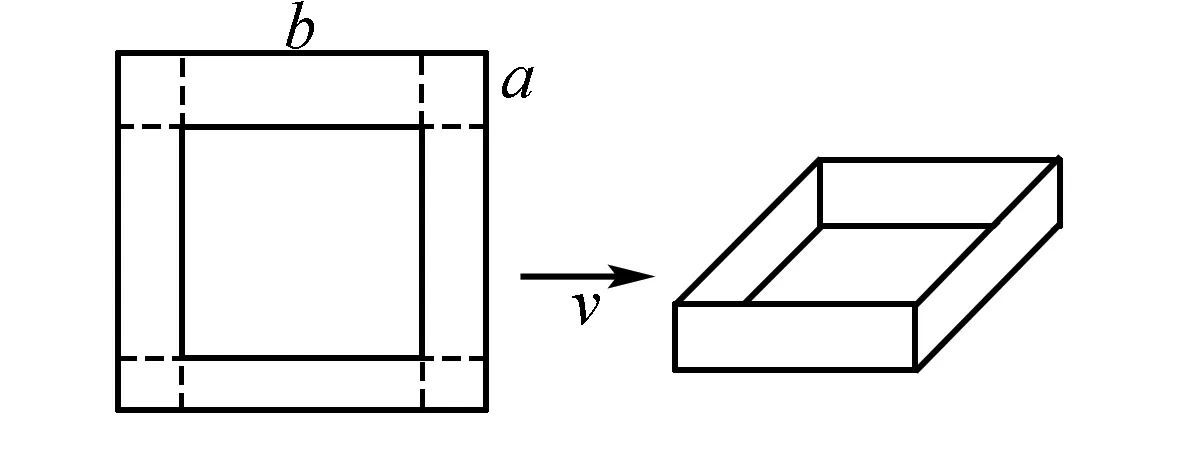
如图所示，b为大正方体的边长，虚线部分为被剪去的小正方形，a为小正方形的边长，将剩下部分折成如右图所示无盖长方体.问：如何才能使所得无盖长方体的容积V最大呢？

由上图知无盖长方体容积：

V=(b-2a)2×a

(1)

该问题就转化成含有两个变量的极值求解问题.运用初中所学数学知识，采用直接法求解该问题具有很大难度.作者经过思考采用如下迭代法解决该问题.

二、解题思路和迭代的初值步长

根据已知条件，该题目中a和b的关系一定满足下式：b>2a.

(2)

分别讨论在b取不同值(10，20，30，40，50)的情况下，a取何值(1，2，3，4，5)才能使体积最大.该过程得到的最大值(精确到个位)误差较大，为了得到更精确的解，作者又进行了一次循环计算，将解精确到小数点后一位.

得到在a和b取不同值的情况下方程的极大值点，然后，将得到的点用折线图的形式表示出来，发现a和b成线性关系，求出该直线斜率，即得到最终答案.

三、求解过程

1.假设b=10，得到表1所示结果

表1 b=10

从表1得出，a=2时体积最大，考虑计算精度，将答案精确到小数点后一位，则得：

表2

所以b=10时a=1.7，体积最大.

2.假设b=20，得到表3所示结果

表3 b=20

从表3得出，a=3时体积最大，同理，将答案精确到小数点后一位，则得：

表4

所以b=20时a=3.3，体积最大.

3.假设b=30，得到表5所示结果

表5 b=30

从表5得出，a=5时体积最大，同理，将答案精确到小数点后一位，则得：

表6

所以b=30时a=5，体积最大.

4.假设b=40，得到表7所示结果

表7 b=40

从表7得出，a=7时体积最大，同理，将答案精确到小数点后一位，则得：

表8

所以b=40时a=6.7，体积最大.

5. 假设b=50，得到表9所示结果

表9 b=50

从表9得出，a=8时体积最大，同理，将答案精确到小数点后一位，则得：

表10

所以b=50时a=8.3，体积最大.

6.总结以上五步结果，可得表11所示结果

表11 a、b、V之间关系

根据表11可以画出以下直线：

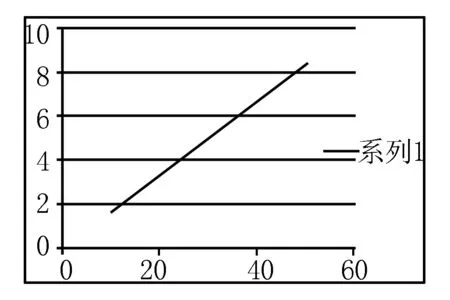
由图中明显可以看出，a、b成正比例关系，需要确定该比例系数.取各比值的平均值作为比例系数.

(3)

所以，当a和b满足如式(4)所示关系时，得到的长方体体积最大.

a=0.167b(4)

本文利用程序设计的思路，经过五次外部迭代过程，两级嵌套内部迭代，最终得到该数学模型的极大值.通过该模型的求解过程，作者初步掌握了程序设计的思想，为以后的学习奠定了基础.

参考文献：

[1]罗预练. 浅谈初中数学中函数与动点形成图形的极值[J]. 数学学习，2016.