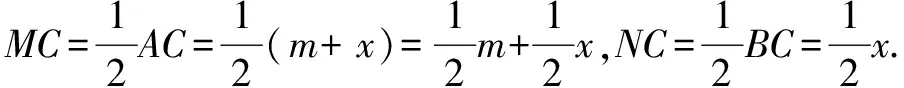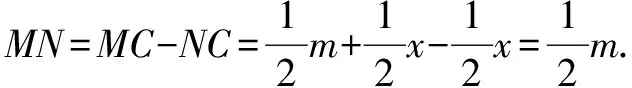一道习题引发的教学思考
2018-05-09李永树
李永树
(重庆市中山外国语学校 404500))
(原题呈现)已知:如图1,∠AOB=70°,∠BOC=30°,求∠AOC的度数.
解析∠AOC=∠AOB+∠BOC=70°+30°=100°.
一、注重变式,融合核心知识
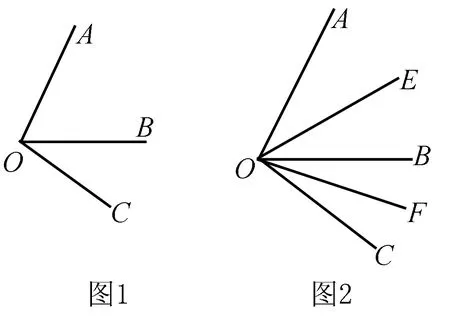
变式1 已知:如图2,∠AOB=70°,∠BOC=30°,OE,OF分别为∠AOB、∠BOC的角平分线,求∠EOF的度数是多少.
解析∵OE是∠AOB的平分线,
又∵OF是∠BOC的平分线,

∴∠EOF=∠BOE+∠BOF=35°+15°=50°.
变式2 已知:如图3,∠AOB=70°,∠BOC=30°,OE,OF分别为∠AOC、∠BOC的角平分线,求∠EOF的度数是多少.
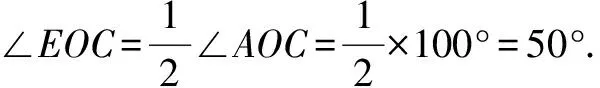
又∵OF是∠BOC的平分线,
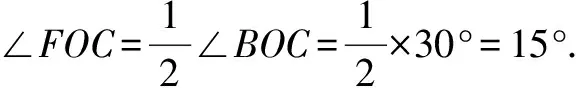
∴∠EOF=∠EOC-∠FOC=50°-15°=35°.

二、注重变式,渗透数学思想
1.整体思想
变式3 已知:如图4,∠AOC=100°,OE,OF分别为∠AOB、∠BOC的角平分线,求∠EOF的度数.

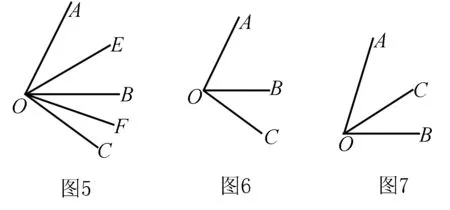
变式4 已知:如图5,∠EOF=50°,OE,OF分别为∠AOB、∠BOC的角平分线,求∠AOC的度数.
解析∵OE是∠AOB的平分线,∴∠AOB=2∠BOE.又∵OF是∠BOC的平分线,∴∠BOC=2∠BOF.∴∠AOC=∠AOB+∠BOC=2∠BOE+2∠BOF=2(∠BOE+∠BOF)=2∠EOF=2×50°=100°.
2.分类讨论思想
变式5 已知:∠AOB=70°,∠BOC=30°,求∠AOC的度数.
解析此题无图,分情况讨论:
情况一:OC在OB的下方时,如图6.
∠AOC=∠AOB+∠BOC=70°+30°=100°.
情况二:OC在OB的上方时,如图7.
∠AOC=∠AOB-∠BOC=70°-30°=40°.

综上所述,∠AOC的度数是100° 或40°.
变式6 已知:∠AOB=70°,∠BOC=30°,OE,OF分别为∠AOB、∠BOC的角平分线,求∠EOF的度数.
解析此题无图,分情况讨论:
情况一:OC在OB的下方时,如图8.
∵OE是∠AOB的平分线,

又∵OF是∠BOC的平分线,
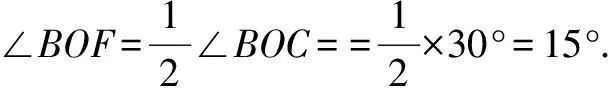
∴∠EOF=∠BOE+∠BOF=35°+15°=50°.
情况二:OC在OB的上方时,如图9.
∵OE是∠AOB的平分线,

又∵OF是∠BOC的平分线,
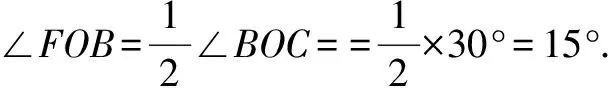
∴∠EOF=∠EOB-∠FOB=35°-15°=20°.
综上所述,∠EOF的度数是50° 或20°.
3.参数思想
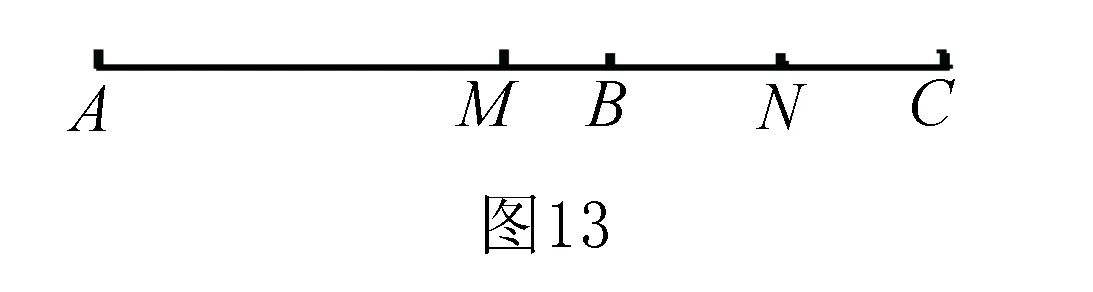
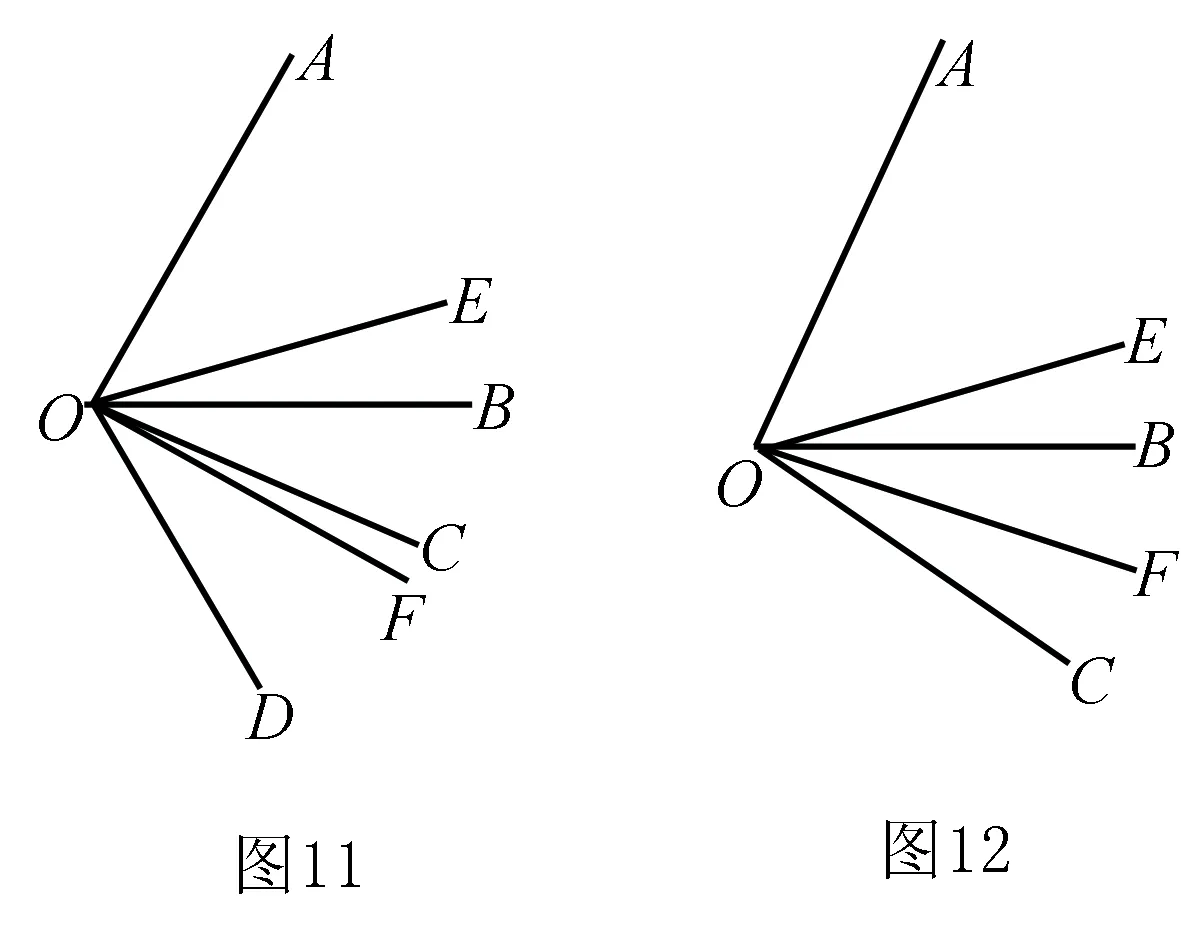
变式7 已知:如图10,∠AOB=70°,∠COD=30°,OE,OF分别为∠AOC、∠BOD的角平分线,∠COD绕点O顺时针旋转x°(0 解析∵∠AOC=∠AOB+∠BOC=70°+x, ∠BOD=∠BOC+∠COD=30°+x, 又∵OE,OF分别为∠AOC、∠BOD的角平分线, 4.方程思想 变式8 已知:如图11,∠AOB=70°,∠COD=30°,OE,OF分别为∠AOC、∠BOD的角平分线,∠COD绕点O顺时针旋转x°(0 解析∵∠AOD=∠AOB+∠BOC+∠COD=70°+x+30°=100°+x, 又∵OE,OF分别为∠AOC、∠BOD的角平分线, ∵∠AOD+∠EOF=6∠COD, ∴(100°+x)+50°=6×30°,解得:x=30°. 变式9 已知:如图8,∠EOF=50°,∠BOC=30°,OE,OF分别为∠AOB、∠BOC的角平分线,求∠AOB的度数. ∵OE是∠AOB的平分线,∴∠AOB=2∠BOE. 又∵OF是∠BOC的平分线, ∴∠BOE=∠EOF-∠BOF=50°-15°=35°, ∴∠AOB=2∠BOE=2×35°=70°. 变式10 已知:如图12,∠AOB=70°,∠BOC=x,OE,OF分别为∠AOC、∠BOC的角平分线,求∠EOF的度数.并说明∠EOF的大小与∠AOB和∠BOC的关系. 解析∵∠AOC=∠AOB+∠BOC=70°+x, ∵OE是∠AOC的平分线, 规律:∠EOF的大小总等于∠AOB的一半,与∠BOC的大小无关. 变式11 线段的计算与角的计算存在密切联系,计算方法可以借鉴.请根据变式10设计一道以线段为背景的计算题,写出解答过程并总结出一般规律. 试题:如图13,已知线段AC,B为AC上一点,AB=m,M、N分别为AC、BC的中点,求MN的长. 解析设BC=x,AC=AB+BC=m+x. ∵M、N分别为AC、BC的中点, 规律:线段MN的大小总等于线段AB的一半,与线段BC的大小无关. 总之,在教学中教师要注重知识的系统整理,注重试题的多变,充分挖掘试题之间的内在联系,形成知识链、题型组,强化学生对数学思想和方法的理解与运用,从而更好地培养学生分析问题、解决问题的能力和学习数学的浓厚兴趣. 参考文献: [1]蒋世香. 培养学生数学素养的意义及措施[J]. 科学咨询(科技·管理),2017(04).

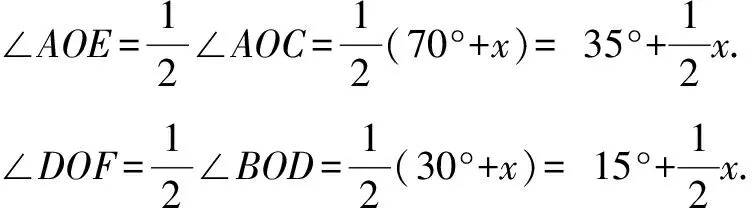
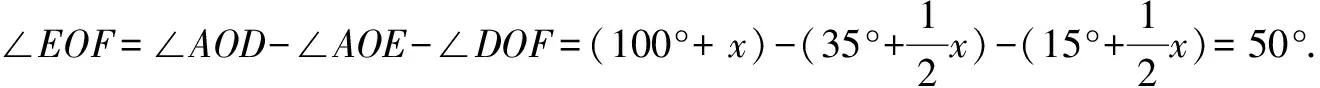
三、注重变式,强化灵活运用
四、注重变式,探究一般规律



五、注重变式,创新设计编题