关于高中物理动量问题的探究
2018-05-09肖凯
肖 凯
(湖南省长沙市雅礼中学 410007)
一、动量与动量守恒定律
十七世纪初,意大利物理学家伽利略首先引入“动量”这个名词.法国数学家笛卡儿继承与发展了伽利略提出的动量概念.1644年,他在《哲学原理》中写道:“当一部分物质以两倍于另一部分物质的速度运动,而另一部分物质却大于这部分物质两倍时,我们应该认为这部分的物质具有相同的运动.”笛卡儿是把物质的多少和速度的乘积作为动量——物体“运动的量”的量度的.但由于那时“质量”的概念尚未建立,而且笛卡儿还未考虑到速度的方向性,因此动量的意义还未十分明确.
1687年,英国物理学家牛顿首次明确地定义了质量的概念,紧接着就定义了动量.他说:“运动的量是用它的速度和质量一起来量度的.”在这里,牛顿关于运动量度的思想是同笛卡儿、惠更斯等一致的,但因为建立了质量的概念和明确了速度的方向性,把动量作为一个矢量.因此,这是物理学的发展史上第一次真正建立了动量的概念.
动量可以按照以下公式计算:P=mv(1)
式中,P为物体的动量,其含义为:物体的动量等于物体质量与其速度的乘积.
高中物理的两大守恒定律,其中之一就是与动量相关的动量守恒定律.在讨论动量守恒定律之前,我们需要认识另一个物理量:冲量—I.冲量表述了对质点作用一段时间的积累效应的物理量,其表达式可以写为:I=F·Δt.和动量是状态量不同,冲量是一个过程量.
根据牛顿第二定律:F=ma(2)
等式两边同乘Δt,有F·Δt=m·a·Δt=mΔv=ΔP
上式的含义可以表述为:物体所受合外力的冲量等于它的动量的增量.这也就是我们常说的动量定理.
根据动量定理,我们很容易得出下列两个结论:
1.“物体”如果不受到外力,那么这个“物体”的动量守恒.
2.动量与力具有方向性,所以动量守恒也具有方向性.
二、高中物理的碰撞问题
碰撞的定义:在极短时间内,至少2个物体相遇而使物体的运动状态发生变化.
按轨迹分为正碰和斜碰,按动能是否损失分为弹性碰撞与非弹性碰撞.弹性碰撞遵循动能守恒与动量守恒定律;非弹性碰撞只遵循动量守恒定律,(非弹性碰撞包括完全非弹性碰撞).
无论是弹性碰撞还是非弹性碰撞,都遵循动量守恒定律.下面以简单的碰撞模型来解释碰撞过程中的动量守恒规律.

图1
1.弹性碰撞

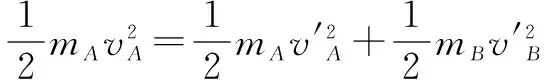
根据①②,解得


由③④两个等式分析以下几种特殊情况:a)若mA=mB则有vA′=0,vB′=vA,两物体速度交换;b)若mA≪mB则vA′≈-vA,vB′=0,A物体以方向相反的相等速度撞回;c)若mA≫mB时,vA′≈vA,vB′=2vA,A物体速度基本不变,而B的速度以2vA飞出.
2.对心碰撞与非对心碰撞
中学阶段主要研究对心碰撞,即碰撞之前的两物体速度在同一直线上,碰撞后速度仍会沿着这条直线,也叫正碰.对于非对心碰撞,可以将动量分解,以向量的形式表现,根据同一方向上的动量守恒规律,列式求解.
三、例题分析
1.弹性碰撞模型
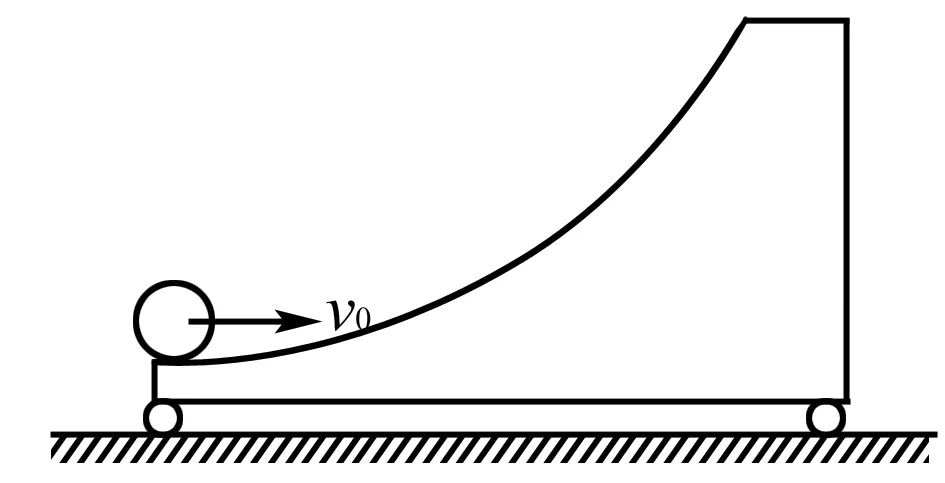
图2
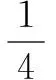
解析初看这道题,若从力这一方面去解题,似乎是不可能的,是一个曲面受力情况不清楚.所以我们应从能量角度来分析,抓住临界状态.
一开始,小球m会在曲面上不断“爬升”,因两物体的相互作用,小车开始加速,某一时刻,小球达到最高点,两者达到共速,然后小球m向下滑,因相互作用,小车仍会加速,直到小球回到出发点.
最高点时:能量守恒,有
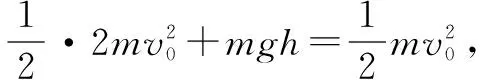
将之看成一个质量为m的小球去“碰撞”另一个质量为m静止的小球,没有能量损耗,即能量守恒,所以这是一个“弹性碰撞”,根据前面的结论,速度为v0的小球去碰撞另一个等质量且静止的小球,交换速度,所以很容易得出正确答案B、C.
2.非弹性碰撞模型
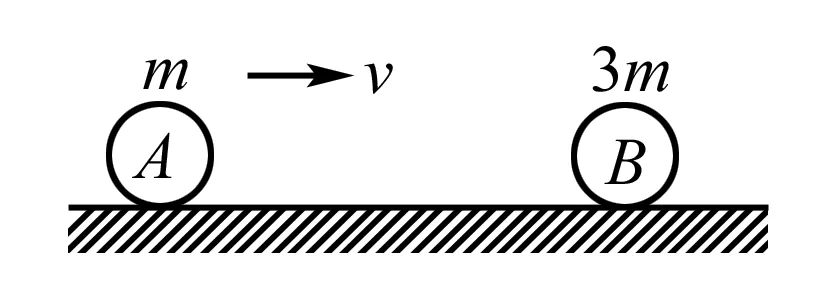
图3
例2 如图3所示:质量为m,速度为v的A球与质量为3m,静止的B球发生正碰,碰撞可能是弹性,也可能是非弹性的,因此碰撞后的B球速度允许有不同的值,请你论证:碰撞后B球的速度可能是( ).
A.0.6 m/s B.0.4 m/s C.0.2 m/s D.0.1 m/s
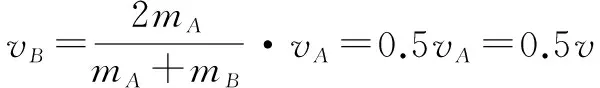

3.微观世界中的动量

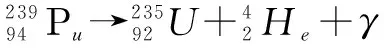
已知质量亏损Δm=mpu-(mu+mα),则E=Δmc2,设E0为释放出的能量,全部转化为动能.
设Eu与Eα为铀核动能与α粒子的动能.
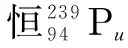


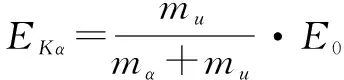
参考文献:
[1]满建真,黄国华,李越.高中生物理成绩的影响因素及相关对策[J].亚太教育,2016(17):143.
[2]曹炜航.应用于高中物理“图象法”解题中的图象斜率探析[J].中国新通信,2017(01):136.
[3]王亦扬.分析高中物理实验的学习对策[J].科技资讯,2017(01):139.
