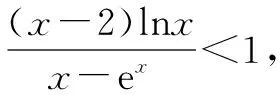例析导数压轴题中严格不等式的证明
2018-05-09贺航飞唐盛彪
李 宁 贺航飞 唐盛彪
(海南省海南中学 571158)
资金项目:本文为海南省教育科学“十三五”规划立项课题《基于云平台教学的数学特优生校本课程开发实践》(课题编号:QJZ13516009)研究成果之一.
严格不等式f(x)>g(x)的证明是导数压轴题中一类常见的问题. 这类问题的表达式中通常会混合多种类型的函数,解法灵活且具有一定的难度,能很好考查学生的洞察力.
例题当x>0时,证明不等式:ex>lnx+2.
本文以此题为例,从不同方向入手探索这类问题的解题策略.
一、借助隐零点估计最值来证明f(x)-g(x)>0
要证明f(x)>g(x),只需证明f(x)-g(x)>0,此时只要求出f(x)-g(x)的最小值与0比较即可. 但是通常导函数的零点不能求出,可以对零点采取设而不求的策略来估计f(x)-g(x)的最小值.


又当x∈(0,x0)时,h′(x0)<0;当x∈(x0,+)时,h′(x0)>0. 从而x0是h(x)的极小值点,也是最小值点,即
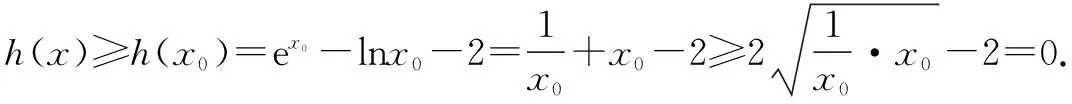

变式1 当x>0时,证明不等式(x-2)lnx+1>0.
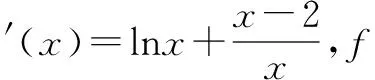
又当x∈(0,x0)时,f′(x0)<0;当x∈(x0,+)时,f′(x0)>0. 从而x0是f(x)的极小值点,也是最小值点,即设则从而g(x)在(1,2)上单调递减,故g(x) 计算出f(x)min,g(x)max,一旦f(x)min>g(x)max成立,则必有f(x)>g(x),此时的函数不等式相对比较弱. 还有一种情形是,f(x)min=g(x)max,但两边取最值的条件不同,也有f(x)>g(x). 回到例题,不等式的两边均无最值,此时得设法等价改造使得能求最值. 以上思路是在中间找一个常数作为中介来证明f(x)>g(x). 类似地,我们也可以通过适当放缩在中间插入一个函数作为中介来证明f(x)>g(x). 函数不等式ex≥x+1及其等价形式lnx≤x-1是常用的放缩工具,也是例题的背景. 证法3 首先证明不等式ex≥x+1. 设f(x)=ex-x-1,则f′(x)=ex-1. 当x∈(-,0)时,f′(x)<0;当x∈(0,+)时,f′(x)>0. 从而x=0是f(x)的极小值点,同时也是最小值点,即f(x)≥f(0)=0,故ex≥x+1,等号成立当且仅当x=0. 当x>-1时,由ex≥x+1得x≥ln(x+1). 从而当x>0时,x-1≥lnx,等号成立当且仅当x=1. 于是当x>0时,ex>x+1=(x-1)+2≥lnx+2,ex>lnx+2得证. 参考文献: [1]林国夫. 2013年高考导数综合应用中的“隐零点”[J]. 中学数学杂志,2013(9):49-52.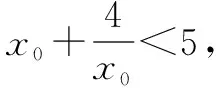
二、通过f(x)min>g(x)max来证明f(x)>g(x)


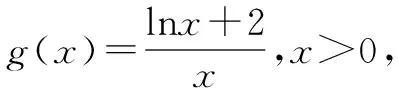
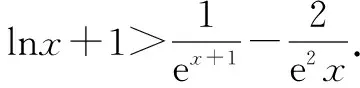

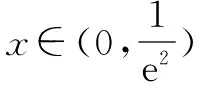

三、通过f(x)>h(x)>g(x)来证明f(x)>g(x)