范畴论对集合论的超越——“数学基础”研究的比较分析

孔祥雯，郭贵春

(山西大学 科学技术哲学研究中心，山西 太原 030006)

数学哲学的研究离不开数学学科的繁荣发展，数学基础为数学学科的发展提供了坚固保障。集合论对数学概念的统一解释奠定了其在数学基础研究中的核心地位，范畴论对数学结构的阐释启发了新的基础研究思路，撼动了ZFC*策梅洛-弗兰克尔的公理化集合论(Zermelo-Fraenkel Set Theory)，包含选择公理(AC)时记为ZFC。长期以来的基础定位。那么范畴论数学基础的研究起点是什么？范畴论数学基础具有怎样的研究特点？根据研究性质，范畴论数学基础能否充分地阐释集合论？以这些问题为契机，我们可以分析范畴论数学基础相对于集合论数学基础具有的研究优势，并论证范畴论在数学基础研究中超越集合论的可能性。

一 范畴论数学基础的研究起点

集合论对无穷的全新解读在数学史上具有里程碑式的意义，对数学对象的解释又促使其在数学基础研究中率先占据了核心地位。范畴论基于对数学结构的阐释跻身数学基础研究，成为集合论数学基础的有力竞争者。阐明范畴论数学基础的研究起点，为探求数学基础研究中范畴论对集合论的超越奠定基础。

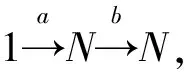
阐明范畴论数学基础的研究起点，实际上是对范畴论数学基础进行理论溯源，如此，既可明晰范畴论被提议为数学基础的动因，又有利于深入分析范畴论数学基础的研究特点。

二 范畴论数学基础的研究特点

范畴论基于对数学结构的阐释，创立了一种不同于集合论的数学基础研究进路。聚焦范畴论数学基础的研究特点，比较分析范畴论与集合论在数学基础研究中存在的差异性，探究范畴论数学基础相对于集合论数学基础的研究优势。

(一)重构研究重心

范畴论与集合论最显著的区别在于集合论的研究重心是数学对象，范畴论则将研究重心转向了数学对象间的关系。研究重心的不同揭示了范畴论与集合论数学基础的本质差异，直接决定了数学对象在数学基础研究中的重要性。在集合论数学基础的研究思想中，数学的研究对象是集合，也就是说，集合可以表示所有的数学对象。那么表示不同对象的集合有什么不同，它们是由什么确定的呢？集合论者通过集合所包含的元素来确定集合，但由于表示同一个数的集合其包含的元素可能存在不同，使得集合会面临选择上的困难。以范畴论为数学基础的研究思想中，数学研究的是结构，而结构是对象之间的关系所形成的，因而范畴论研究的重心在于对象之间的关系，范畴论中的概念如态射、函子、自然转换、同构、伴随等都是对关系的表述。在范畴中，对象只需满足其中的态射关系即可。范畴论者不需要指出、也不关心对象由什么构成，并且单个对象在范畴中没有作为个体的研究意义，对象间的关系才是范畴论的研究重点。通过以上分析可知，范畴论重构了数学的研究重心。相对于集合论数学基础而言，范畴论数学基础的研究优势在于其通过结构来阐释数学，无须考虑数学对象的具体构造。

(二)重建关系表述

集合论中涉及的关系表述都是直观的；范畴论则是将包含关系的数学系统抽象为数学结构，重建理论中的关系表述。我们通过分析理论中涉及的关系来具体解释表述的不同。在集合论中，元素与集合之间的从属关系，集合与集合之间的包含关系实质上都是在确定元素是否属于某一集合，是直观的。范畴由对象和态射组成，本质上是态射决定了对象，进而确定了范畴。范畴论中的关系都包含在结构中，对数学系统进行抽象，就能得到一个由关系组成的数学结构。在关系的表述过程中可以得出，集合论中的关系都是依附于集合的，因为只有集合确定了，才能谈及集合涉及的从属关系、包含关系；反之，范畴是依附于关系的，是关系确定了范畴。就理论中的关系而言，拉夫尔(F. William Lawvere)曾表示，“集合论基于二元的从属关系，范畴论基于三元的复合关系(如图表的交换性)。通过这种方式，范畴论专注于结构，集合论则专注于恒等式……。在范畴论中对象之间的关系表示结构的形成，尤其当确定出箭头的上域时，就能明确区分包含映射与恒等映射。集合论则不能完全地区别f：R→R与f：R→N”[1]。显然，范畴论是借由关系来理解数学，故而对关系的表述更加精细、全面。

(三)重聚理论阐述的对象域

相较于集合论，范畴论可描述的对象域更显宽广。考虑理论阐述的对象域首先要解析集合和范畴的定义。集合的元素都是具体对象，集合中的映射一般通过函数表示；由范畴的定义可知，范畴的对象不需要包含元素，态射也不必是函数。例如，一个有关形式逻辑系统的范畴，该范畴的对象是逻辑系统中的公式，态射是从前提公式到结论公式之间的推导关系。[2]可见，范畴的定义更一般化。麦克莱恩(Saunders Mac Lane)对集合论提出了质疑，认为集合论不能阐述两类范畴：(1)由于自我指涉的悖论，集合论不能阐述涉及结构全体的范畴，如所有集合的范畴、所有群的范畴，所有范畴的范畴等；(2)任意两个给定的范畴所形成的指数范畴BA，[1]该范畴是函子范畴，其中的态射是函子之间的自然转换。然而，我们可以通过单位态射、恒等态射等态射的使用将集合看作范畴中的对象。结合上述分析可知，集合论对数学对象域的描述并不充分，范畴论重新聚焦理论阐述的对象域，凭借定义的一般化阐述了更大范围的数学对象域。

(四)重释数学结构

与集合论对数学结构的阐释相比，范畴论的阐释方式更符合数学结构主义的研究宗旨，能够更高效地重释数学结构。数学哲学家为结构的阐释提供了多种思路。布尔巴基学派(Bourbaki School)最早完成了数学结构的定义，并选用集合论的语言阐释数学结构。拉夫尔、麦克拉蒂(Colin McLarty)等支持范畴论数学基础，主张使用范畴论的语言阐释数学结构。从范畴论与集合论对数学结构的阐释中可对比得出两点：(1)在集合论的阐释中，交换群与模表示的是同样的结构，也就是说集合论对任意给定的数学结构有多种不同的解释模式；而表示相同结构的范畴是同构的，范畴论对数学结构的阐释保持在恒定的语法中。(2)集合是由元素组成的，故而集合论对结构的阐释始终包含与结构无关的性质。范畴论研究的是对象间的关系，不关注对象由什么组成。在范畴论的阐释中，数学对象都处于特定的关系中，不存在与结构无关的性质。显然，范畴论对数学结构的重新阐释与结构主义的思想更加契合。阿沃弟(Steve Awodey)对此表示，“相比于型论以及集合论的构造，范畴论支持的结构主义进路更为坚定、强大以及恒定”[3]124。应该说，范畴论更适用于数学结构主义的研究进路。

综上，范畴论数学基础具有不同于集合论数学基础的研究特点，这源于范畴论自身的构造方式。范畴的定义是建立在关系而不是数学对象之上的，如此决定了范畴论数学基础的研究重心，以及对关系的抽象表述方式，也同时决定了范畴论所描述的对象域相对于集合论而言更为宽广。结构是范畴论通往数学基础之路的重要媒介，范畴论在阐释数学结构中表现出的恒定与契合突出了其相对于集合论的研究优势。

三 范畴论数学基础的研究性质

范畴论与集合论被同时提及必定源于对数学基础争论的探讨。尽管是在不同的时期被提议为数学基础，但这两种理论还是具有明显的竞争关系。究竟是集合论能够为包含范畴论在内的数学提供基础，还是范畴论能够阐释所有的数学结构后来者居上呢？显然，点对点的分散式研究不足以回答这一问题，需要从整体角度出发进行解答。因此，我们将从研究特点转向研究性质，并依据范畴论数学基础的研究性质，探索范畴论数学基础超越集合论数学基础的可能性。

(一)集合论数学基础对范畴论阐释的不充分性

集合论数学基础的研究思路是将所有的数学对象都表示为集合；范畴论数学基础则认为数学研究的是结构，范畴论可以阐释所有结构。使用集合论数学基础阐释范畴论就是要解释数学中的结构。贝纳塞拉夫(Paul Benacerraf)曾指出数不是集合；结构主义者主张数与数之间的关系是满足了某些特定条件的结构，数是该结构中的某个位置。按照这样的理解，集合论必定不能解释数的结构，自然也无法诠释所有的数学结构。范畴由对象和态射构成，如果将范畴看作对象，范畴间的函子看作态射，又可以形成新的范畴。考虑到范畴的构造，格罗滕迪克(Grothendieck)对范畴进行了区分，将可以用集合表示的范畴称作小范畴。显然，范畴论中还存在一些集合论无法解释的大范畴。面对这一难题，集合论者想要通过借助一些理论为所有范畴提供集合论的阐释。一种思路是借助格罗腾迪克全域(universe)，使那些不能称作小范畴的数学结构借助不可达基数表示为累积分层(Cumulativehierarchy)中更高级别的层级。但是这其中借助的不可达基数，其存在超出了ZFC公理系统的包含范围。因此，集合论采用的这种阐释方式并不成立。另一种思路源自布拉斯(Andreas Blass)，他指出不需要假定不可达基数的存在，“假定当变量遍及所有集合或遍及所有小集合时，每个一阶陈述都有同样的意义。换言之，所有小集合的全域是所有集合全域的子结构”[4]。这种假设是想要借助反射原理(Reflectionprinciple)完成，如果依据大范畴得到了某个结论，那么小范畴自然也有同样的结论。我们认为，利用反射原理并不能完成这样的假设。因为如果不假定不可达基数的存在，集合的语言就不能表述大范畴，范畴的全域与集合的全域没有包含关系，自然不能将集合中的结论应用于大范畴。综上，我们有理由认为集合论数学基础的研究性质并不能完全地适用于范畴论。

对于集合论数学基础能否阐释范畴论，还有一种简单的回答，即范畴论与集合论是相互独立的，范畴论不需要集合论作为数学基础。按照这样的思路，无论集合论能否充分地阐释范畴论，都是不必要的。纵观数学史的发展，集合论在范畴论出现之前已取得辉煌的成就，确实不需要依赖范畴论。此外，范畴论的出现比较滞后，但是这并不表明范畴论就必然依赖于集合论的相关概念和理论。林博(Øystein Linnebo)及佩蒂格鲁(Richard Pettigrew)在“范畴论作为自主的基础”[5]一文中论证了范畴论在逻辑、概念上的自主性，表明了范畴论相对于集合论的独立性。由此可见，范畴论确实不需要集合论的阐释，它可以依据公理系统断言自身存在，范畴论的对象也不需要集合论的表述，因为范畴论关注的是对象之间的关系，不考虑对象的组成。因此，范畴论自身的发展不需要借助任何有关集合论的概念、性质等。

简言之，集合论数学基础的研究性质的确可以适用于部分范畴，但不适用于所有的范畴。由此可知，集合论数学基础对范畴论的阐释是不充分的。

(二)范畴论数学基础对集合论的阐释及深化

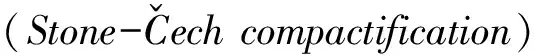
更重要的是，范畴论不仅可以阐释集合论，而且能以范畴的方式处理集合，对集合论进行进一步深化。以集合范畴为例，将所有的集合看作对象，集合间的函数关系作为态射，就形成了集合范畴。值得注意的是，范畴与集合的深入联系不仅仅局限于集合范畴，而是朝向更一般化的拓扑斯。应该说，范畴论与集合论在拓扑斯公理系统中的联系最为紧密。拓扑斯的出现归功于格罗滕迪克，他认为空间属于范畴，而一般的拓扑空间可以表示为拓扑斯。当然，拓扑斯的涵盖范围远不止此。20世纪70年代，拉夫尔与蒂尔尼(Myles Tierney)对拓扑斯进行了一阶公理化，丰富了拓扑斯公理系统。拓扑斯公理是在一般的范畴公理上添加两个涉及终对象和幂集的公理。显而易见，所有的拓扑斯都是范畴，确切地说，拓扑斯是特殊的范畴。在拓扑斯公理系统中，经典数学的概念、性质、证明等依然存在及成立，只是不同于原先的构造方式。集合范畴作为最一般的拓扑斯，其对集合的处理方式与公理化集合论中的处理方式必然不同。但是，公理化集合论中的定义和证明在拓扑斯中都是适用的，并且使用拓扑斯公理中的幂集、子集等概念可以替代集合论中的力迫法、对称子模型等；另外，拓扑斯还能作用于集合论中一些结论的证明，例如科恩(Paul Cohen)的独立性证明、选择公理的独立性证明。简言之，范畴论不仅能够阐释集合论中的概念、性质、定理等，而且能够通过结构的方式对集合论进一步深化，使其不同于公理化集合论的构造，更加方便、有效地证明数学理论。

总之，集合论数学基础在阐释范畴的过程中表现出了不充分性，无法阐释全体数学。与之相比，范畴论表现出了一定的竞争优势，不仅范畴论数学基础的研究性质可作用于集合论，而且范畴论还能以结构的方式处理集合论的相关内容。由此，我们认为相较于集合论的数学基础，范畴论数学基础在描述数学的过程中具有一定的优势，值得数学哲学家继续深入研究。

四 范畴论数学基础的研究意义

范畴论数学基础的发展深刻地冲击了集合论长期以来的数学基础地位，凭借对数学结构的阐释范畴论在数学基础研究中脱颖而出，以结构的方式更加清晰地建构数学。剖析范畴论数学基础的研究特点及研究性质，有助于阐明范畴论不同于集合论的基础研究进路。通过具体的分析比较，范畴论数学基础展现出了一定的研究优势。为此，我们将探求范畴论数学基础的研究意义，彰显其深远的研究价值。

(一)研究内容上，范畴论的基础进路扭转了传统基础研究对数学对象的单一关注，使数学转向了对关系的研究

从对象到对象之间的关系，这种转向一方面揭示了范畴论被提议为数学基础的动因，另一方面表明了范畴论是不同于集合论的数学基础思路。在结构主义思潮的推动下，数学结构主义在数学哲学中应运而生。结构主义者摒除了以集合论为数学基础的研究思想，尝试以结构的方式建构数学，将数学看作是由结构构成的学科。范畴论的研究重心是对象之间的关系，对数学系统中的关系进行抽象就得到了数学结构，这些数学结构共同作用形成了数学整体，由此产生了从数学到结构再到范畴的基础研究思路，范畴论也因此成为数学基础的有力竞争者，使数学基础研究迈上了新的征程，打破了长期以来以集合论为主的基础研究状态。

(二)研究方法上，范畴论转向了以方法论为主的基础研究思路，超越了集合论以本体论为主的基础研究思路

集合论最显著的基础特征是对数学对象的阐述，主要在本体论的意义上探讨数学基础。范畴论关注对象间的关系，由关系决定该结构中的对象，范畴论确实有本体论上的断言，但是与数学结构相比，数学中的对象显然不是结构主义的研究重心。范畴论的基础特征源自对数学结构的阐释，体现了数学结构主义的研究方法。“我们现在想要确定一种特定的结构主义方法，这种方法是许多当代数学家所共用的。它涉及数学家所做的工作，我们将其称作结构主义的方法论。”[6]考虑到结构主义方法论在数学中的应用以及范畴论与结构的阐述关系，数学哲学家更多的是在方法论这一意义上阐明范畴论的数学基础，为范畴论的数学基础研究提供方法论意义上的论证。

(三)研究思路上，范畴论数学基础遵循着从数学到结构再到范畴的研究思路，这一思路既呈现了范畴论数学基础的理论渊源，也表明了范畴论数学基础不是数学哲学家的任意选择，而是基于数学结构主义思想的合理优选

在数学结构主义的发展过程中，不只有范畴论的结构主义进路，还主要包括先物结构主义及模态结构主义的进路。遗憾的是，先物结构主义无法逃脱认识论的劫难[7]，模态结构主义对结构的模态中立主义态度，使其难以表明数学的可应用性，也难以规避语义学难题。[8]布尔巴基作为数学结构主义的奠基者，试图通过集合论阐释数学结构，但是这一进路并没有行进太远就夭折了。范畴论依据自身的态射、函子及同构等一些概念充分合理地阐释了数学结构，催生了范畴结构主义的研究进路，也由此带动了范畴论数学基础的研究。

(四)研究目的上，随着数学在理论及应用中的不断进步，数学学科日益精进，但始终无法绕开“数学基础”这一研究主题，范畴论数学基础的兴起是解决数学基础争论的一大重要尝试

范畴结构主义进路极大地推动了数学基础的研究，尤其在对数学学科的解读、对数学结构的组织统一等方面。相较于集合论数学基础，范畴论数学基础在研究特点和研究性质上都展现出了一定的优势和研究价值。另外，尽管ZFC面临着选择公理的一致性难题，但在数学基础的研究中似乎仍具有不可取代的地位，一个重要的原因就是，数学尚缺乏一个全新的理论来替代传统的集合论数学基础研究模式。范畴论为数学基础研究提供了这样的可能，它以结构主义方法论为切入点，依据自身语言阐释数学结构，构建了数学基础研究的新模式，使数学基础迈进了一个新的研究阶段。

综上，结合范畴论数学基础的研究起点、研究特点及研究性质可知，范畴论因自身的研究特性、关系表述及对结构的诠释显示了其替代集合论数学基础的可能性，在与集合论的相互阐释中表现出了相对的充分性。基于此，我们认为范畴论数学基础在特定方面超越了集合论的数学基础，是最具发展前景的数学基础进路之一。尽管数学哲学家对范畴论能否替代集合论作为数学基础始终保持相对谨慎的态度，但这种结构主义的进路革新了数学哲学家对数学基础的传统研究模式，使其具有深刻的研究意义。

参考文献：

[1]Horowitz B. Categories within the Foundation of Mathematics[J/OL]. https://arxiv.org/abs/1312.6198v1, 2013-12-21：7-8.

[2]Bondecka-Krzykowska I, Murawski R. Structuralism and Category Theory in the Contemporary Philosophy of Mathematics[J]. Logique & Analyse, 2008, 51(204)：367.

[3]Awodey S. From Sets to Types, to Categories, to Sets[M]// Sommaruga G.Foundational Theories of Classical and Constructive Mathematics. Dordrecht: Springer Netherlands, 2011.

[4]Blass A. The Interaction Between Category Theory and Set Theory[J]. Contemporary Mathematics, 1984, 30：8-9.

[5]Linnebo Ø, Pettigrew R. Category Theory as an Autonomous Foundation[J]. Philosophia Mathematic, 2011, 19(3)：227-254.

[6]Reck E H, Price M P. Structures and Structuralism in Contemporary Philosophy of Mathematics[J]. Synthese, 2000, 125(3)：345.

[7]康仕慧,张汉静.数学本质的先物结构主义解释及困境[J].科学技术哲学研究,2013,30(5)：17.

[8]刘 杰,孙曌莉.赫尔曼的模态结构主义[J].科学技术哲学研究,2015,32(5)：25.