新型二维轮轨耦合单元及OpenSees实现

古 泉,李维泉,国 巍,刘永斗,蒋丽忠,余志武

(1.厦门大学 建筑与土木工程学院，福建 厦门 361005；2.厦门大学 厦门市交通基础设施智能管养工程技术研究中心，福建 厦门 361005；3.中南大学 土木工程学院，湖南 长沙 410075；4.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075)

业内学者[1-3]对车桥耦合问题进行了系统研究，其中二维(竖向)车桥耦合理论和数值方法可归纳为如下三类：(1)子系统迭代求解[4]。将车辆子系统、轨道-桥梁子系统单独建模，通过几何关系和相互作用力的平衡关系协调两个子系统的耦合。(2)浓缩自由度直接求解[5-8]。将车轮的响应(位移、速度和加速度)用与之接触的轨道梁单元的响应基于形函数插值表示，并代入车辆子系统方程得到轮轨作用力，再将该作用力代入轨道-桥梁子系统方程，得到缩减自由度后的系统耦合方程，进行逐步积分求解。(3)耦合系统整体求解。该方法通过构造车辆-轨道耦合单元[9]、车辆-轨道-桥梁耦合单元[10-11]、轮轨耦合单元[12-13]等不同的时变单元，按照“对号入座”法则组装系统的耦合振动方程，进行逐步积分求解。

本文提出一种基于非线性接触关系的新型二维轮轨耦合单元，建立竖向车桥耦合系统有限元模型并进行地震动力分析。该单元有如下优势：(1)易于集成到现有的通用有限元框架，编程难度低；(2)车辆运行中有限元模型无需修改，建模难度小；(3)能够模拟轮轨间非线性接触，可考虑车辆跳轨和轨道不平顺激励的影响。

本文在有限元OpenSees[14]软件平台实现了此单元，该平台拥有丰富的材料库和单元库，在地震响应分析中具备优势，这使得用户能够考虑复杂的工程实际，建立更加精细的车辆模型和轨道-桥梁模型。

1 二维轮轨耦合单元模型

二维轮轨耦合单元所在位置如图1(a)所示，该单元由一个轮节点w和列车行进过程中所有可能与之接触的梁单元节点序列[a,…,i,j,…,q]组成。当车轮运动t时间后，通过几何关系可计算轮轨接触点O与起始节点a的距离为X(t)。

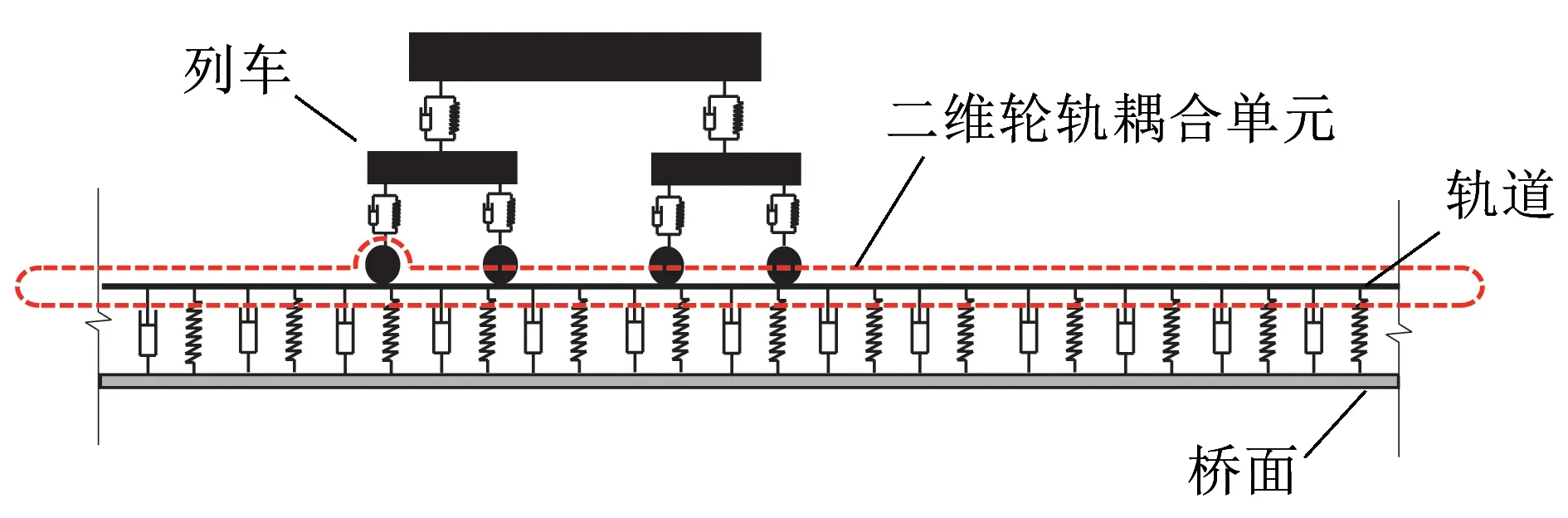
(a)车-轨-桥系统模型

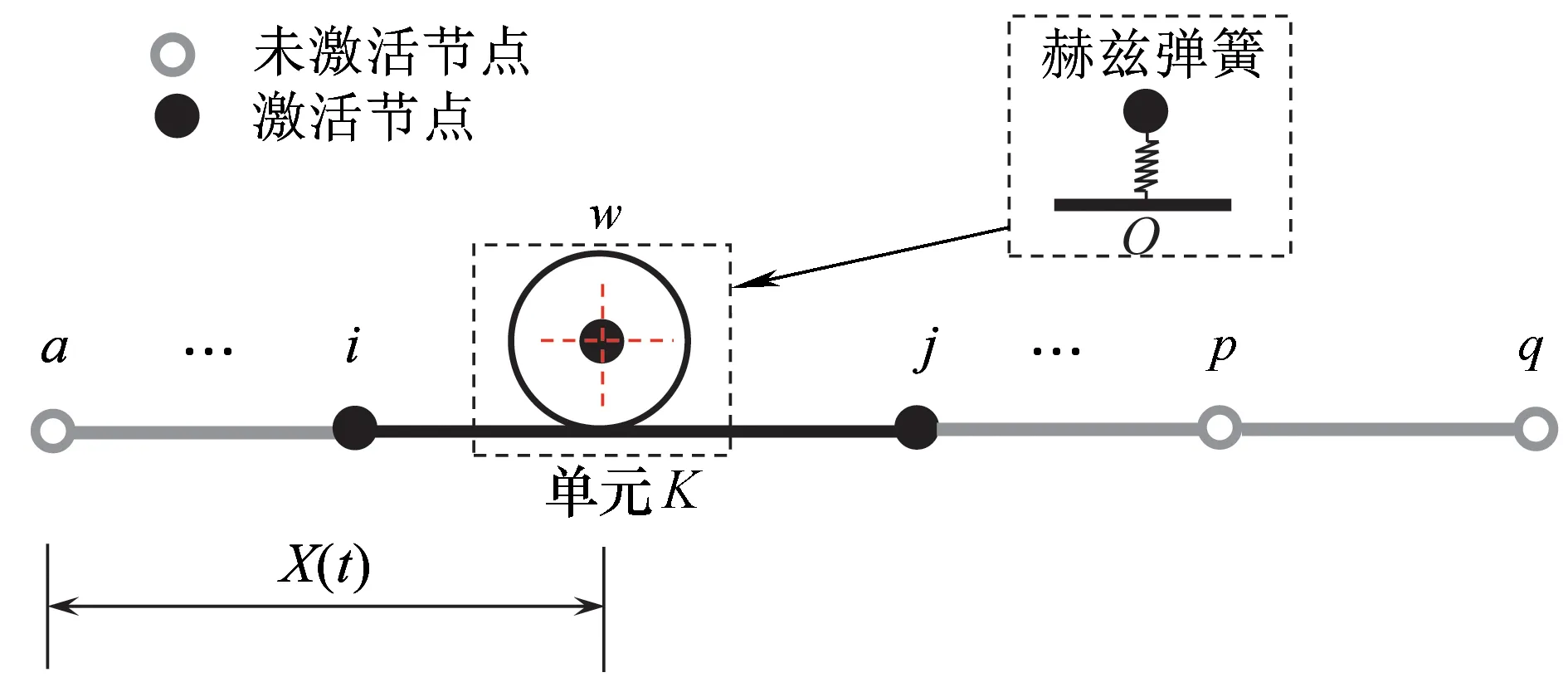
(b)二维轮轨耦合单元模型图1 二维轮轨耦合单元模型及所在位置示意

对于二维问题，忽略轨道梁水平方向的自由度，梁单元仅考虑竖向和转动自由度，车轮仅考虑竖向自由度，因此，二维轮轨耦合单元自由度和内力可表示为

( 1 )

( 2 )

式中：u1为车轮节点竖向位移；R1为车轮节点竖向内力；u2～un为所有可能与车轮接触的梁单元节点位移；R2～Rn为所有可能与车轮接触的梁单元节点内力。

如图1(a)所示，在某一时刻t，车轮行进至单元K处时，二维轮轨耦合单元a、p、q节点内力和对应刚度取值均为0，i、j节点内力和对应刚度取值不为0。因此，为方便推导计算，我们将非接触处的局部节点a、p、q定义为未激活节点，接触处单元K的局部节点i、j定义为激活节点。因此，激活的局部轮轨耦合单元自由度和节点内力定义为

( 3 )

( 4 )

如图2所示，u2～u5和R2～R5分别表示局部轮轨耦合单元激活节点对应的位移和内力。

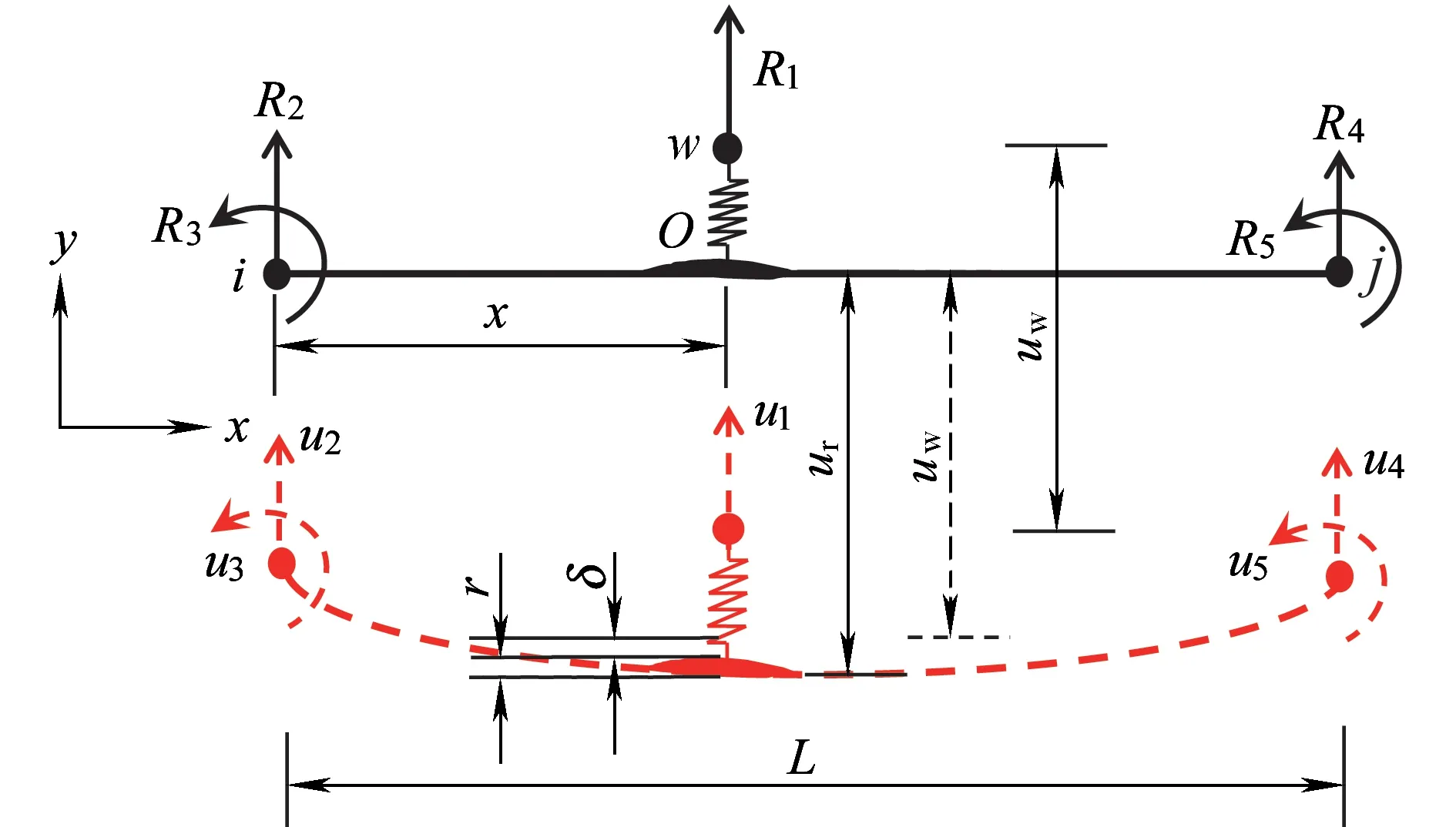
图2 激活的轮轨耦合单元局部节点

1.1 轮轨接触力直接求解

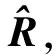
( 5 )

其中

如图2所示，x为轮节点w与激活的轮下轨道梁左节点i之间的水平距离，可通过X(t)求得；L为轮下梁单元长度。

本文基于赫兹非线性弹性接触理论，如图1(b)所示，假定车轮与轨道通过赫兹非线性弹簧连接。当赫兹弹簧刚度取值偏大时，轮轨间相对位移微小，即可将轮轨之间的连接近似为刚性杆连接，模拟密贴接触的情况；当赫兹弹簧取值正常时，轮轨之间的连接视为正常的弹性接触状态，因此可同时考虑轮轨间嵌入和分离两种情况。轮轨之间竖向作用力与嵌入量的关系[1]为

( 6 )

式中：G为轮轨接触常数，m/N3/2，本文选取锥形踏轮面，计算参数表达式为

G=4.57R-0.149×10-8

( 7 )

其中，R为车辆半径，m；δ为轮轨接触处赫兹弹簧压缩量，δ>0为轮轨间存在嵌入量，δ≤0为轮轨脱离。

由赫兹力计算式( 6 )可知，轮轨间赫兹弹簧变形量δ是计算轮轨作用力FH的基础。接触几何关系如图2所示，本文通过车轮节点和轮轨接触处梁单元节点之间的位移差及轨道不平顺值计算轮轨接触处赫兹弹簧压缩量δ。

δ=ur-uw+r

( 8 )

式中：uw为车轮位移；r为接触点处轨道不平顺值；ur为接触点处轨道梁的位移，包含由形函数插值得到的位移，也包含由于轮轨相互作用产生的位移

ur=us+uH

( 9 )

式中：us为插值得到的轮下轨道梁的位移

(10)

uH为赫兹力作用产生的位移

(11)

式中：Kb为梁的柔度。

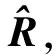
轮轨作用力FH求解步骤如下：

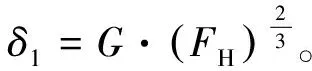
步骤2依据式( 8 )、式( 9 )计算轮轨嵌入深度δ2=ur-uw+r=us+uH-uw+r。

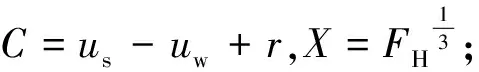
步骤4更新车轮位置，判断车轮是否在单元两端(图3)，构造解的形式。

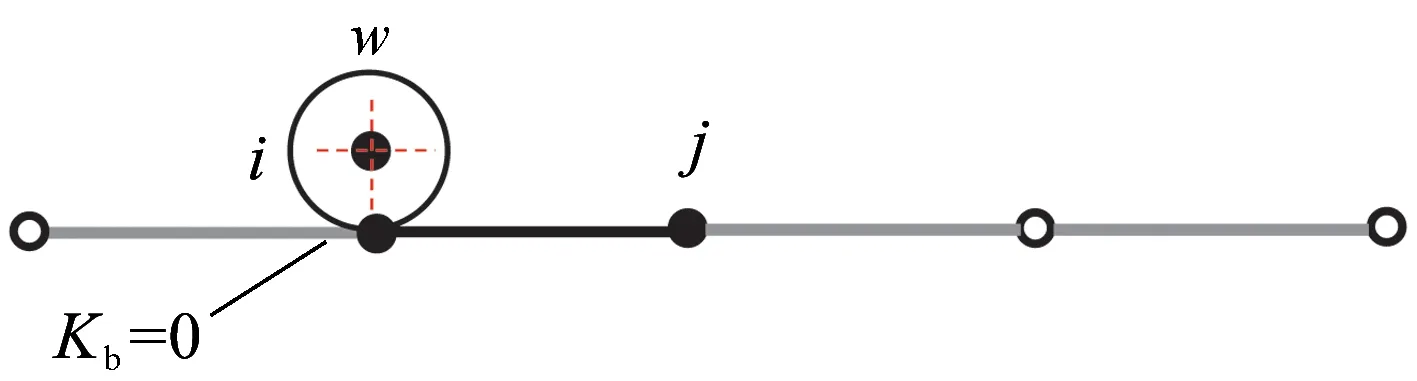
(a) 车轮位于梁单元端部

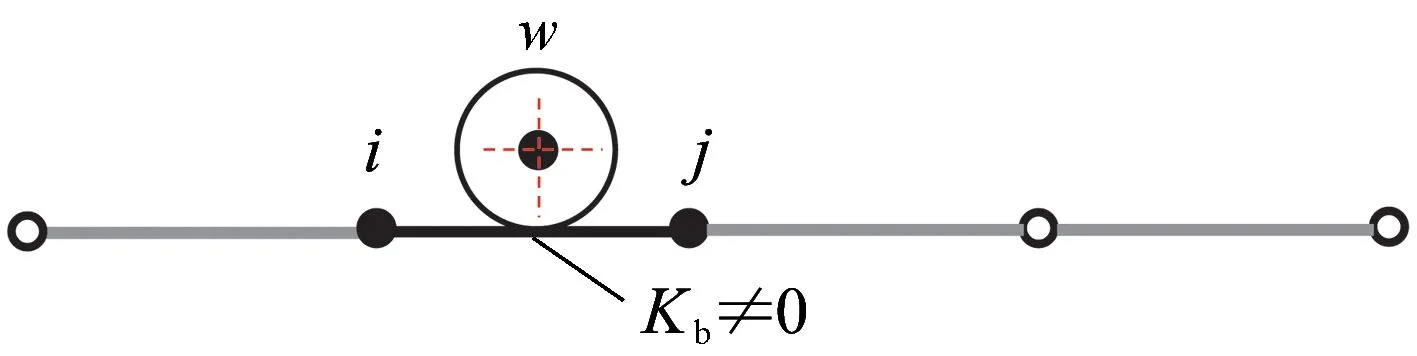
(b)车轮位于梁单元内部图3 车轮位置示意

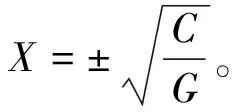
(2)若在单元内部，则Kb≠0，方程为KbX3+GX2-C=0;方程改写为aX3+bX2+d=0。

①计算一元三次方程求解参数

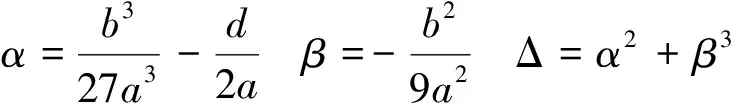
②若Δ≥0且α=0，有实数解

③若Δ=0且α≠0，有两个不同实数解

④若Δ<0，有3个实数解

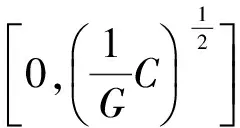
1.2 单元刚度推导

(12)

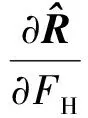
(13)

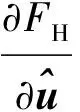
φ=δ1-δ2

(14)

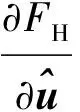
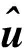
(15)

(16)

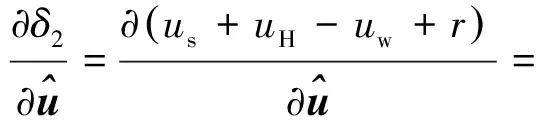
(17)

将式(16)、式(17)代入式式(15)可得

(18)

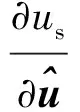
(19)

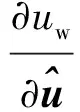
(20)

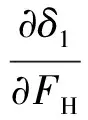
(21)

由式(11)可得赫兹力作用下轮下轨道梁的位移uH与FH的关系

(22)

将式(19)～式(22)代入式(18)中可得

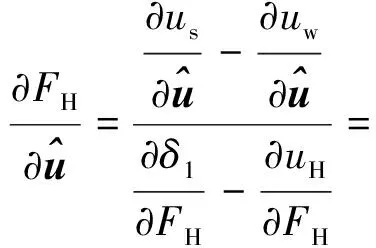
(23)

将式(13)和式(23)代入式(12)即可得激活的局部轮轨耦合单元切线刚度表达式

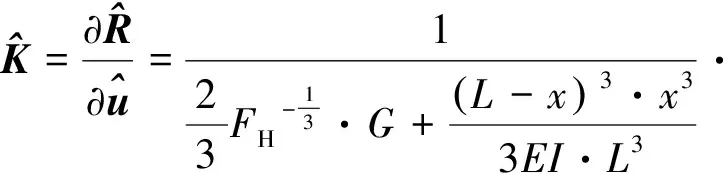
(24)

2 数值验证

为验证本文所提轮轨耦合单元模型的可靠性，进行数值验证。如图4所示，质块近似模拟车辆车体，简支梁模拟桥梁，质块与简支梁之间通过弹簧连接，忽略车轮质量。参数取值[11]如下：质块滑动速度为vc=27.78 m/s，加速度为ac=0 m/s2，简支梁跨度Lb=30 m，弹性模量Eb=2.87×109Pa，截面惯性矩Ib=2.9 m4，阻尼比ζb=0，桥梁线密度mb=2 303 kg/m，质块质量mb=5 750 kg，车轮质量mw取0，连接弹簧阻尼cv=0.0 N·s/m，刚度kv=1.595×106N/m。

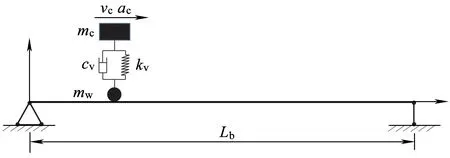
图4 移动质量作用下的简支梁模型

简支梁采用两个二维弹性梁柱单元模拟，不考虑轨道不平顺的影响，将本文分析模型计算所得质块竖向位移dm、加速度am和简支梁跨中挠度db时程曲线与文献[11]对比。如图5～图7所示，基于轮轨耦合滑动单元的有限元模型计算所得的质块竖向位移、竖向加速度和简支梁跨中位移时程曲线与文献[11]中3阶模态解析解(图中标注为解析解)和数值解(图中标注为数值解)非常接近。由于解析解仅考虑了3阶模态，所以时程曲线局部有微小差别。综上可知，本文提出的单元模型可靠，满足工程精度要求。

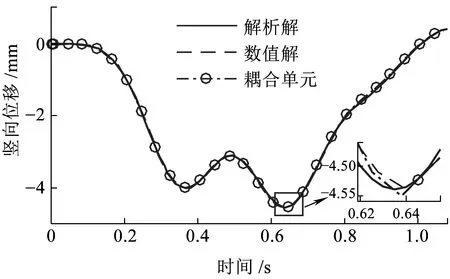
图5 质块竖向位移时程

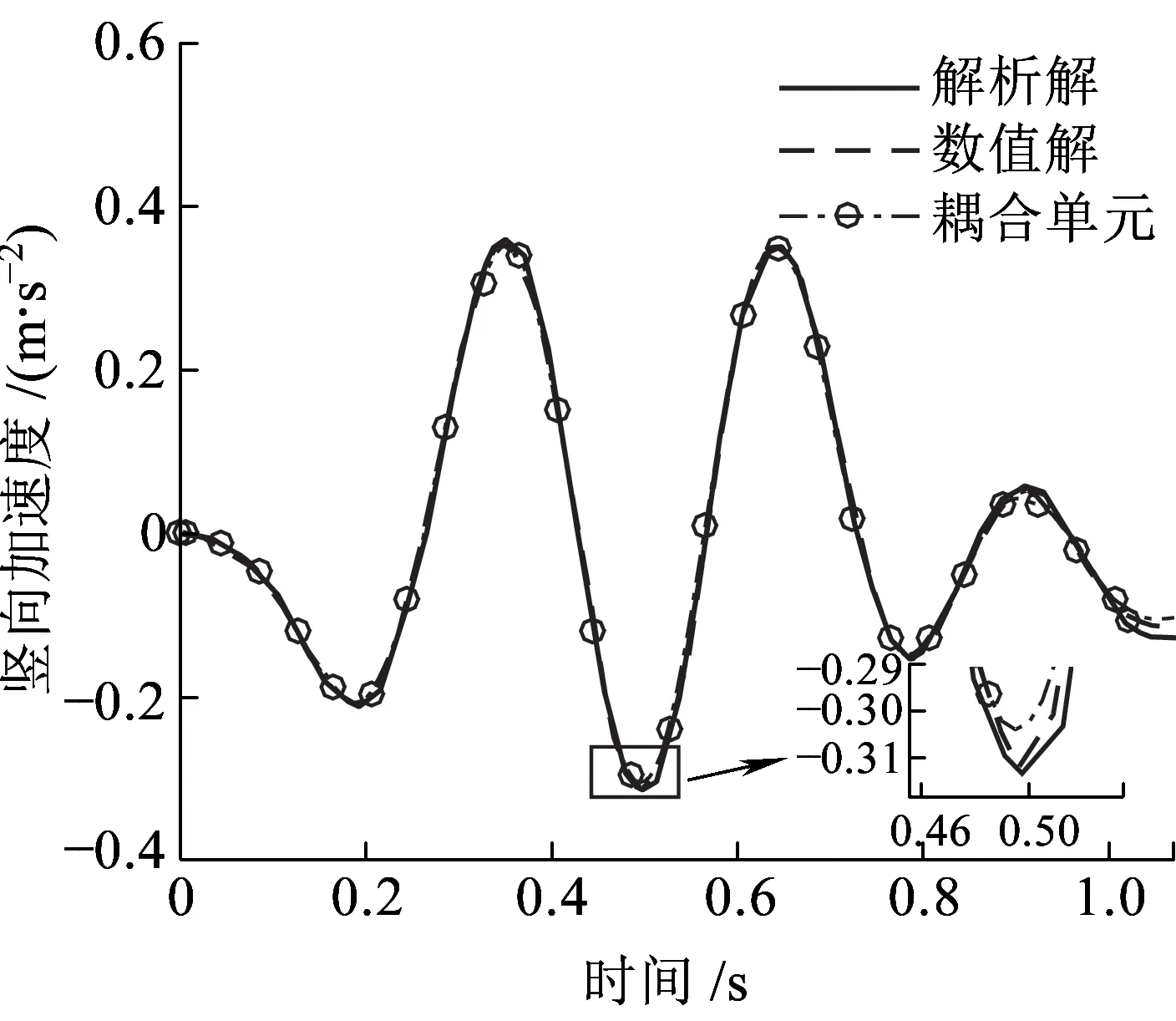
图6 质块竖向加速度时程

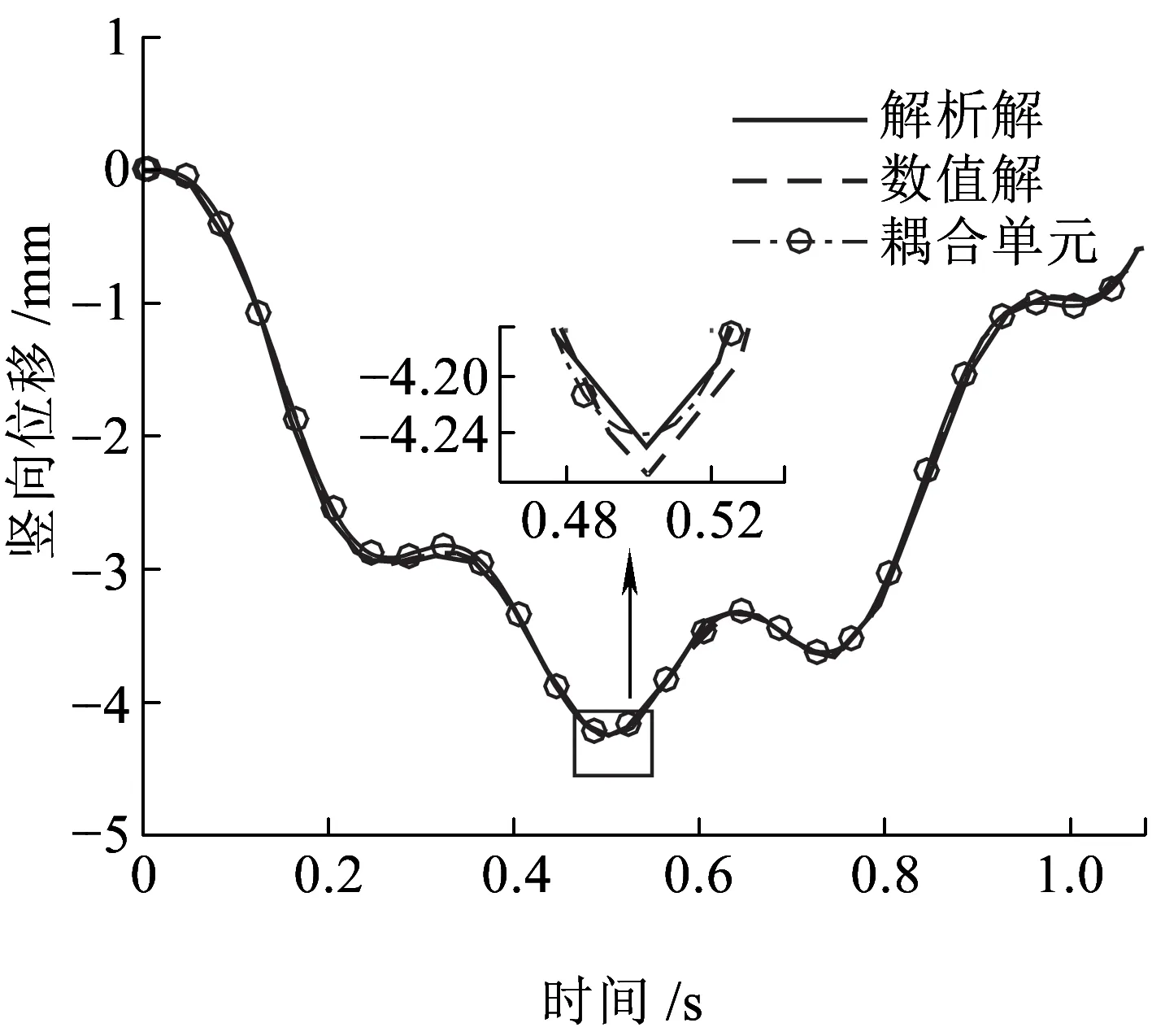
图7 简支梁跨中位移时程

3 车桥系统地震响应分析

本文利用OpenSees丰富的材料库和单元库，将车辆子系统和轨道-桥梁子系统通过OpenSees建模，轮轨耦合系统由本文提出的二维轮轨耦合单元建模，完成竖向车桥耦合系统模型建立。

3.1 车辆系统模型

如图8所示，车辆系统考虑为四轴多刚体体系，该车辆模型由1个车体、2个转向架、4个轮对构成，车轮与转向架间由一系弹簧ktw和阻尼器ctw连接，车体与转向架间由二系弹簧kct和阻尼器cct连接。车体和转向架有沉浮和点头两个自由度，车轮只有沉浮自由度，因此，车辆系统共有10个自由度。建模时，将车体和转向架考虑为刚体，选用两个弹性梁柱单元进行模拟，抗弯刚度取无限大值；车体和转向架之间通过车体端部节点和转向架中部节点连接，选用桁架单元进行模拟。车辆参数[11]见表1。

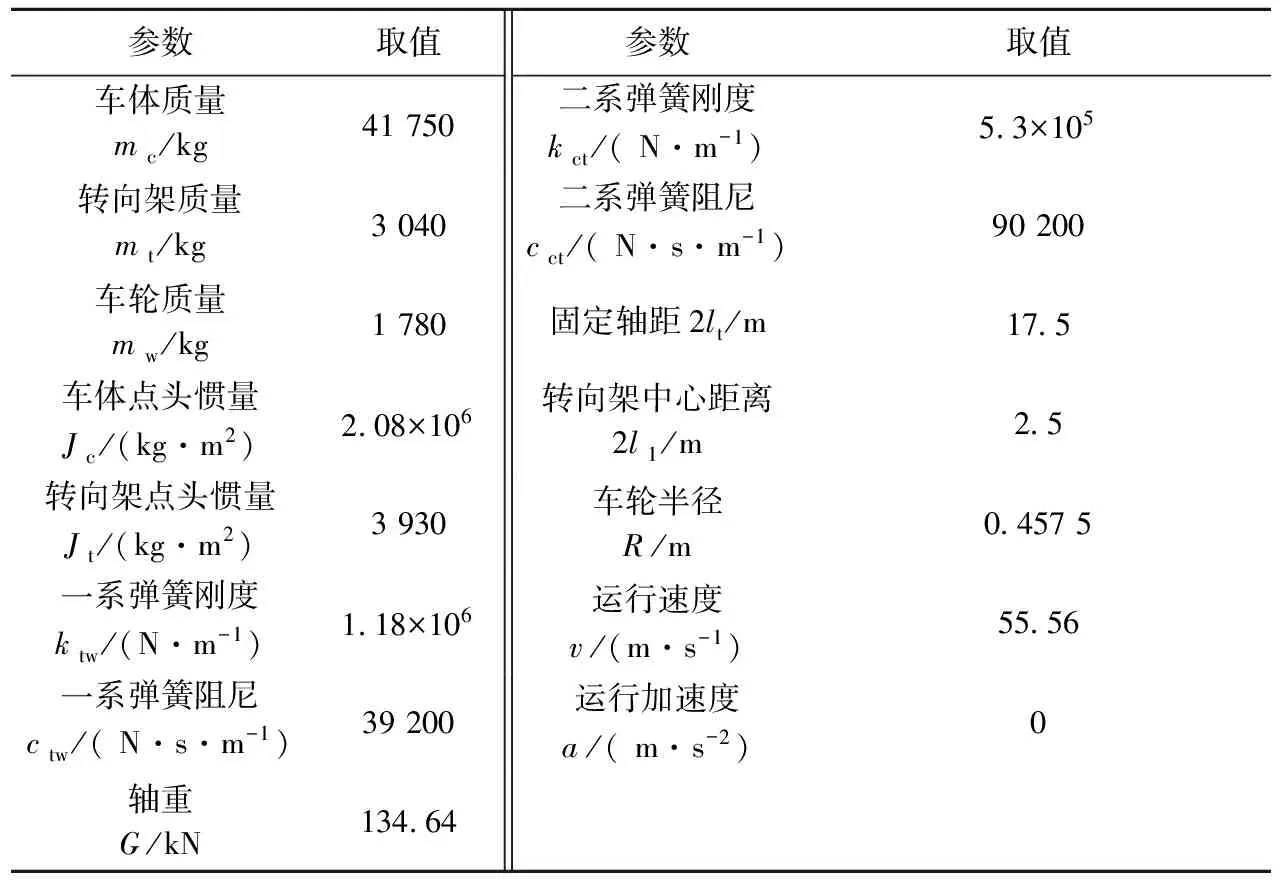
表1 车辆系统参数

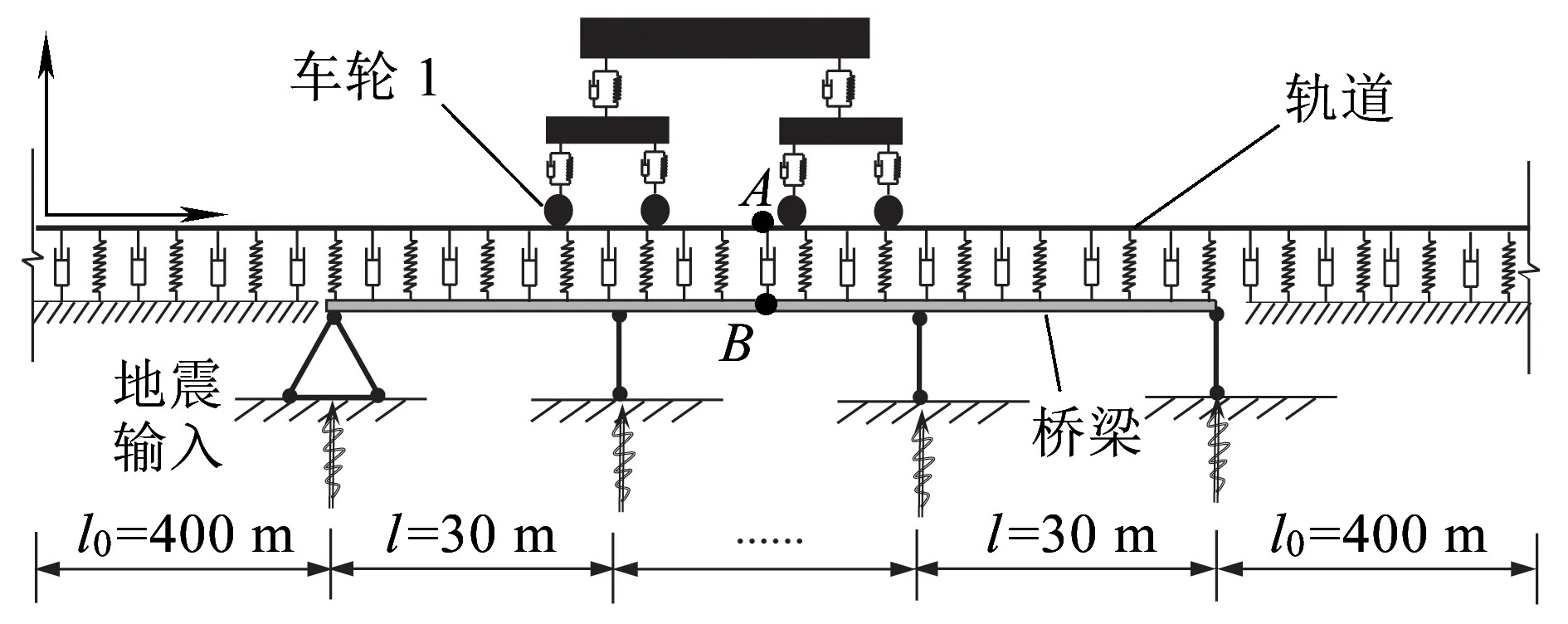
图8 竖向车桥相互作用系统示意

3.2 轨道-桥梁系统模型

如图8所示，在轨道-桥梁系统中，轨道全长1 130 m，桥梁简化为11跨连续梁，单跨长度为30 m。钢轨中部由11跨连续梁支撑，前后端由刚性路基支撑。将轨道与地基、桥梁间的相互作用简化为线性弹簧和阻尼器连接，详细参数[11]见表2。

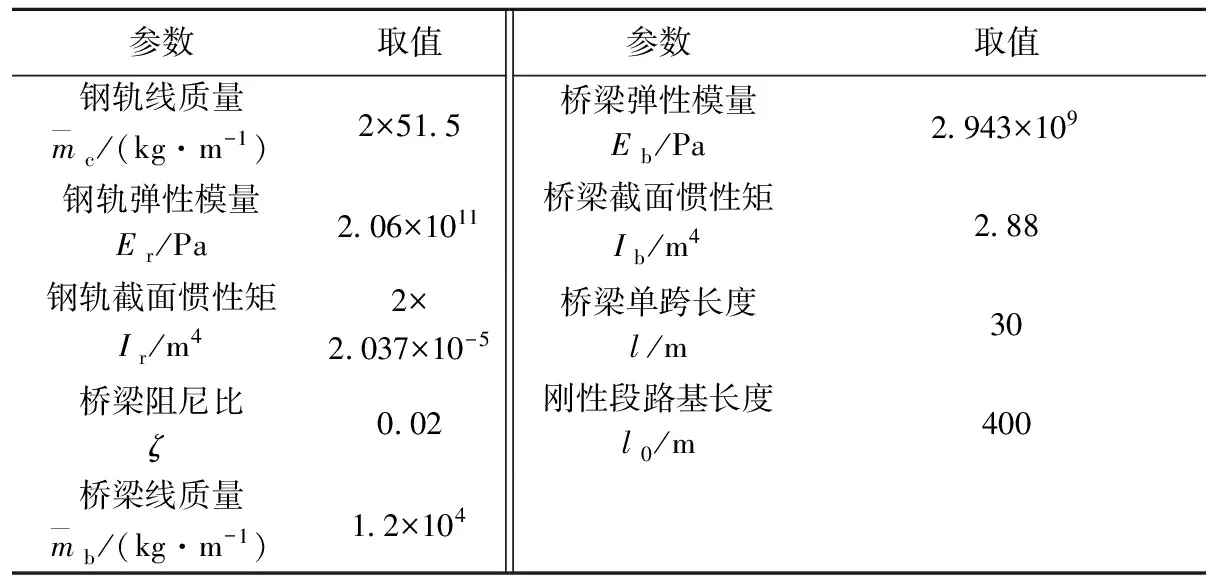
表2 轨道-桥梁系统参数表

3.3 轨道不平顺激励和地震激励输入

本文除考虑自重作用外，还将考虑轨道不平顺激励和地震激励的影响。轨道不平顺r通过式( 8 )方式输入，即将轨道不平顺考虑为轮轨接触处赫兹弹簧变形量的一部分。

(25)

将El Centro地震波竖向加速度作为地震激励作用在轨道梁支承部分，忽略土和结构相互作用，El Centro地震竖向波时程曲线如图9所示，绝对加速度反应谱如图10所示。

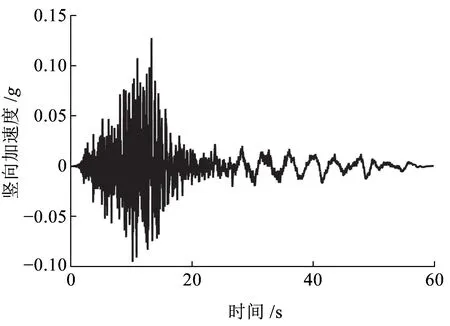
图9 El Centro地震波竖向加速度时程曲线

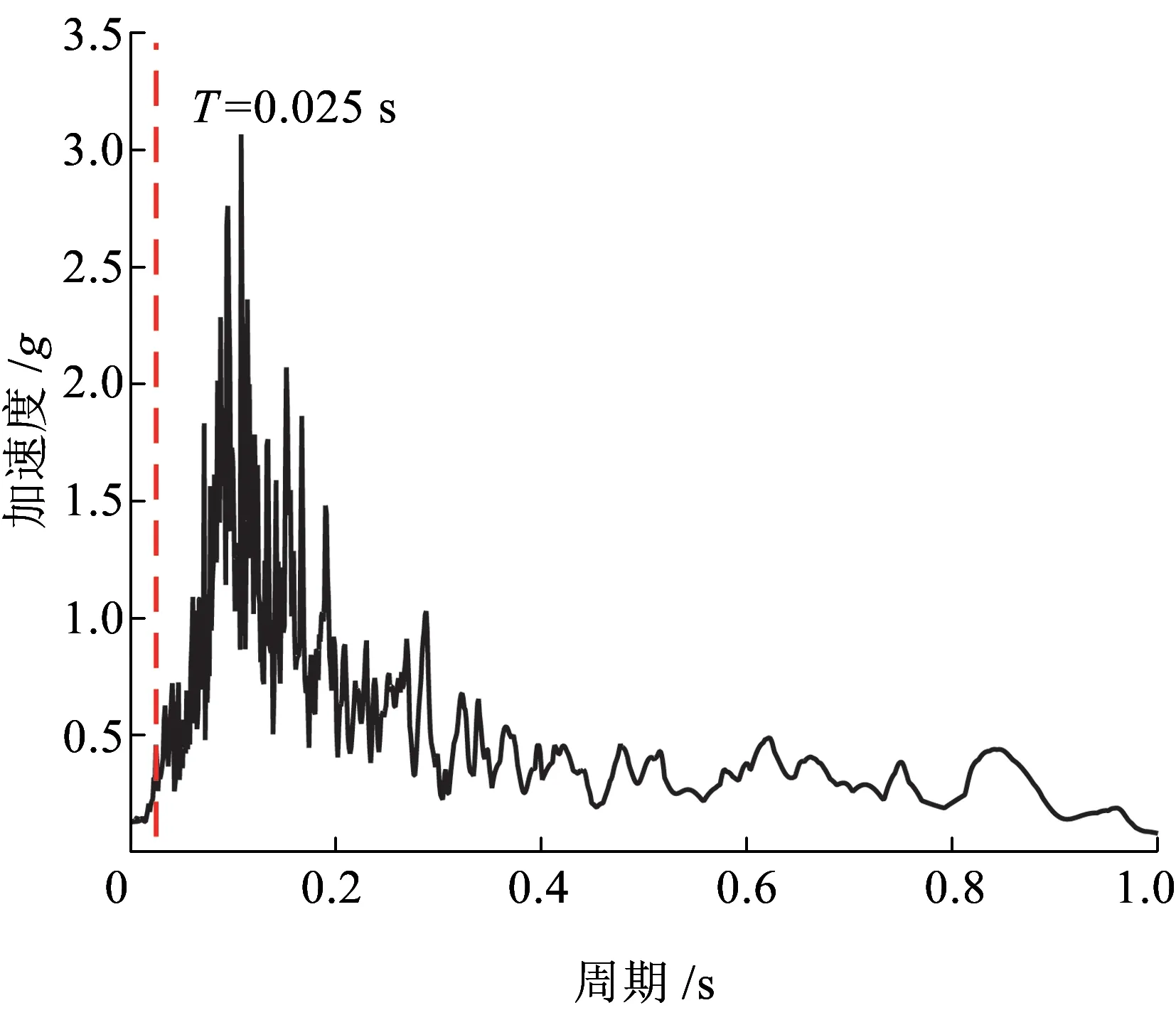
图10 El Centro地震波竖向加速度反应谱

3.4 计算结果分析

本文将车轮1(图8)与轨道作用力(赫兹力)作为车桥动力相互作用强弱的特征指标，为对比动力放大与缩小效应，进一步将该相互作用考虑为赫兹力与车体单轴轴重之比。将钢轨中点A(图8)、桥梁第六跨中点B(图8)及车体的位移和加速度时程曲线作为列车-轨道-桥梁系统动力响应评价，其中，系统位移响应均为消除静力平衡位移后的竖向位移。

列车整车开始通过到离开11跨连续梁的总时间为6.3 s，为了节约篇幅，本文仅选取车轮1(图8)经过轨道不平顺时段(3.32～3.34 s)作为动力响应评价依据，考虑四种工况进行分析，见表3。

表3 计算工况

图11为轮轨作用力与轴重比例系数时程曲线，观察可知，工况Ⅰ和工况Ⅲ的时程曲线基本重合；类似地，工况Ⅱ和工况Ⅳ也基本重合；两组工况下轮轨作用力差异较大。表现为：当车轮1遇到轨道不平顺时(3.32～3.35 s)，轮轨作用力突然增至轴重的约2倍。轨道平顺时，轮轨作用力增减幅度保持在轴重的10%以内，地震作用影响较小。由于竖向轮轨相互作用系统(赫兹弹簧)的第一阶自振频率约为40 Hz(T=0.025 s)，大于所选El Centro波的主要频率(图9)，因此，相比地震作用，轨道不平顺激励对竖向轮轨相互作用的影响更明显。

图12为第6跨桥梁跨中B点竖向位移时程曲线，观察可知，工况Ⅰ和工况ⅡB点竖向位移时程曲线基本重合；类似地，工况Ⅱ和工况Ⅳ也基本重合，两组工况下位移差异较大。这表明，地震作用对B点竖向位移影响明显，相反，轨道不平顺激励作用对其影响较小。图13为第6跨桥梁跨中B点竖向加速度时程曲线，观察可知，四种工况下B点竖向加速度时程曲线幅值有较大差异，峰值由大到小依次为：工况Ⅳ、工况Ⅲ、工况Ⅱ、工况Ⅰ。由此可知，B点竖向加速度对轨道不平顺激励和地震作用都很敏感，轨道不平顺激励会进一步增大B点加速度幅值。

图14为轨道中点A竖向位移时程曲线，观察可知，四种工况下A点竖向位移时程曲线幅值有较大差异。这表明，轨道不平顺激励和地震作用对A点竖向位移影响明显，轨道不平顺激励会改变A点位移幅值。图15为轨道中点A竖向加速度时程曲线，观察可知，工况Ⅰ和工况Ⅲ的A点竖向加速度时程曲线基本重合；类似地，工况Ⅱ和工况Ⅳ也基本重合，两组工况下加速度差异较大。由此可知，地震作用对A点竖向加速度影响较小，而轨道不平顺激励则影响明显。

图16、图17为车体质心竖向位移和加速度时程曲线，观察可知，工况Ⅰ和工况Ⅱ下的车体竖向位移和加速度时程曲线基本重合；类似地，工况Ⅲ和工况Ⅳ也基本重合；两组工况下车体动力响应差异较大。进一步观察表明，在没有地震时车体的位移和加速度都较小。地震作用对车体质心竖向位移影响明显，轨道不平顺激励的影响较小。地震作用和轨道不平顺激励对车体质心竖向加速度均有影响，但地震作用影响更明显。

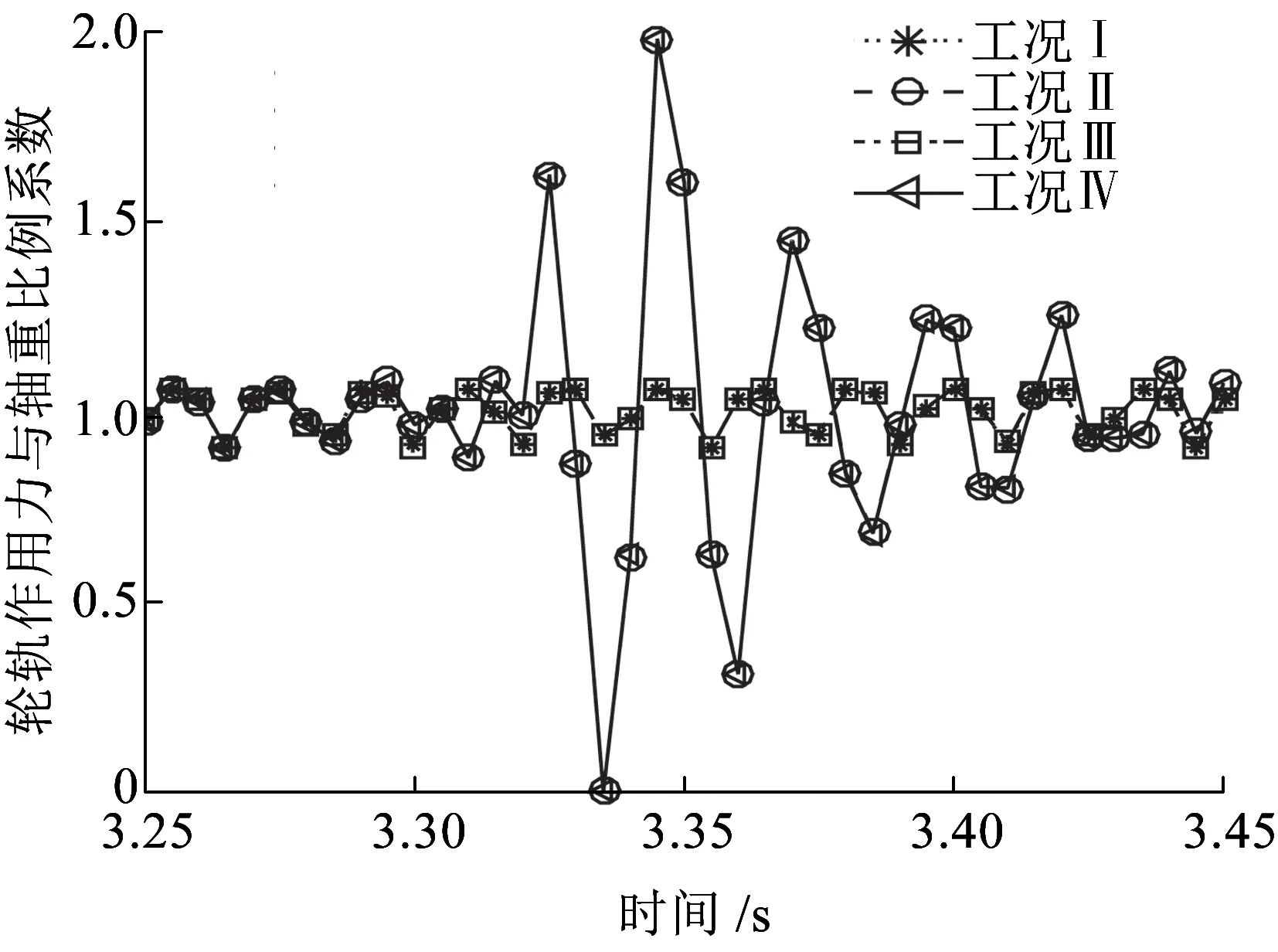
图11 作用力与轴重比例系数时程曲线

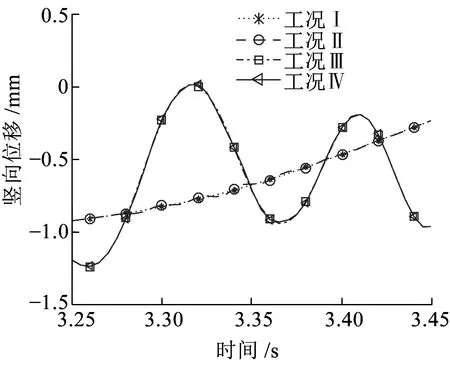
图12 第6跨桥梁跨中B点竖向位移时程曲线

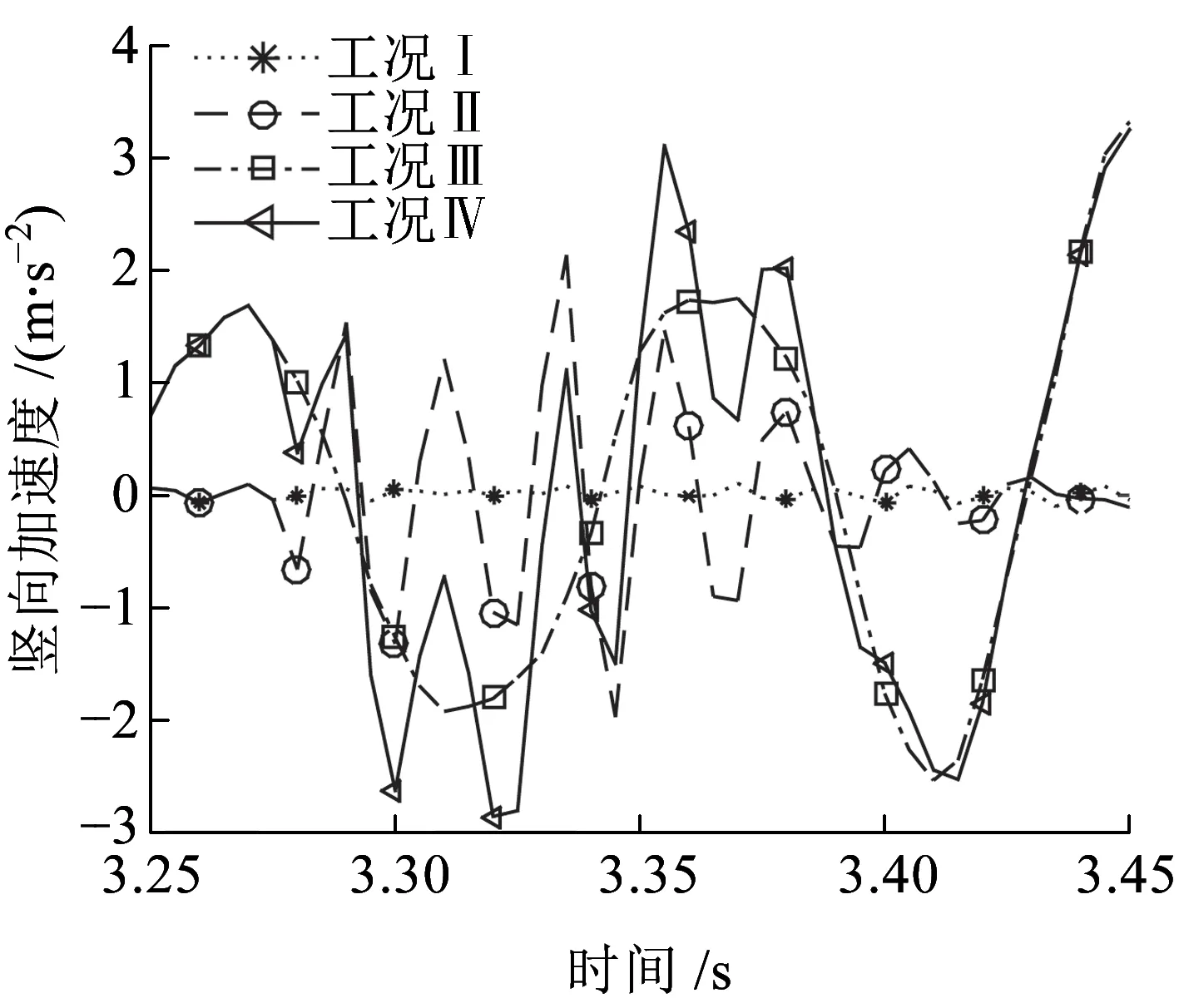
图13 第6跨桥梁跨中B点竖向加速度时程曲线

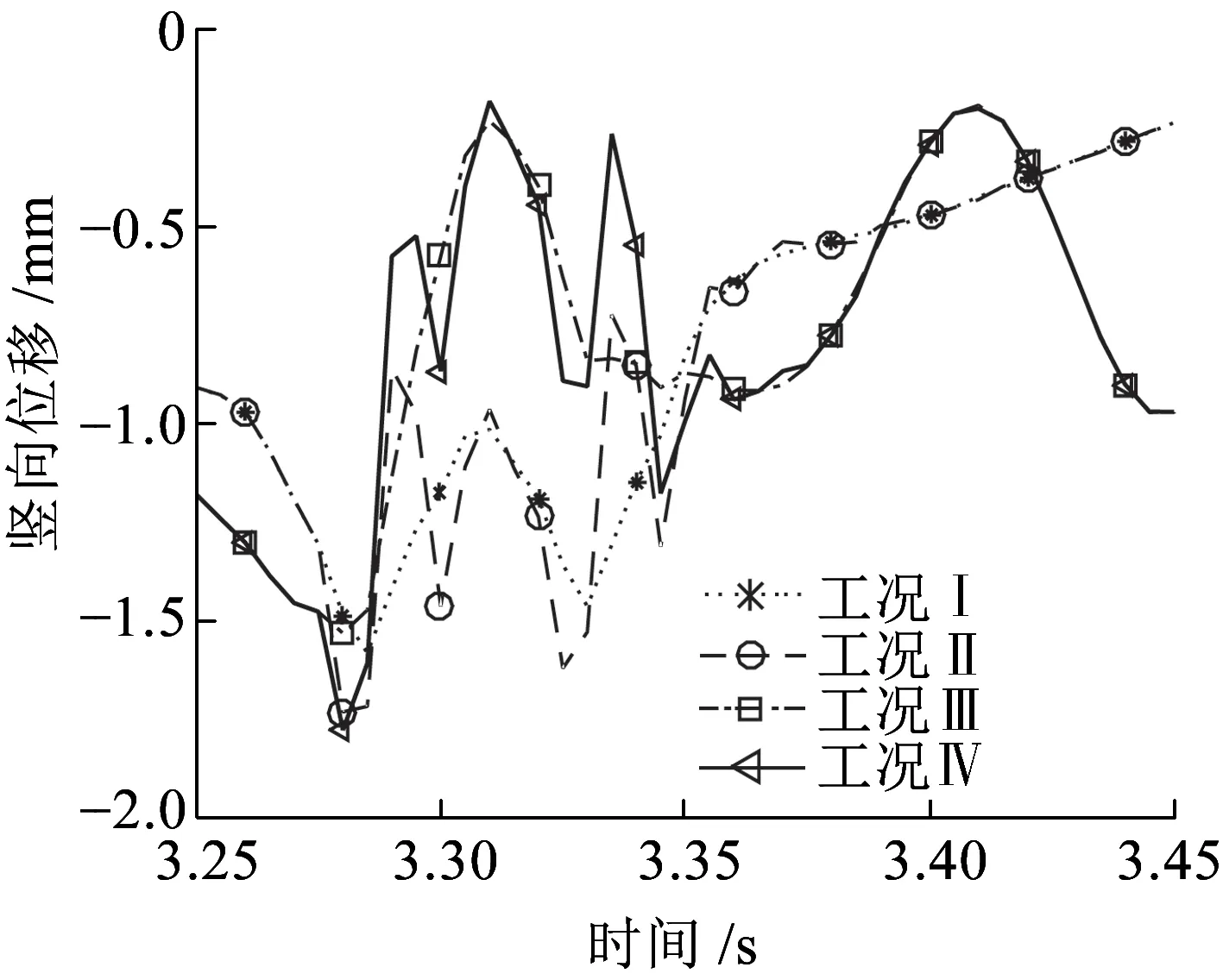
图14 轨道中点A竖向位移时程曲线

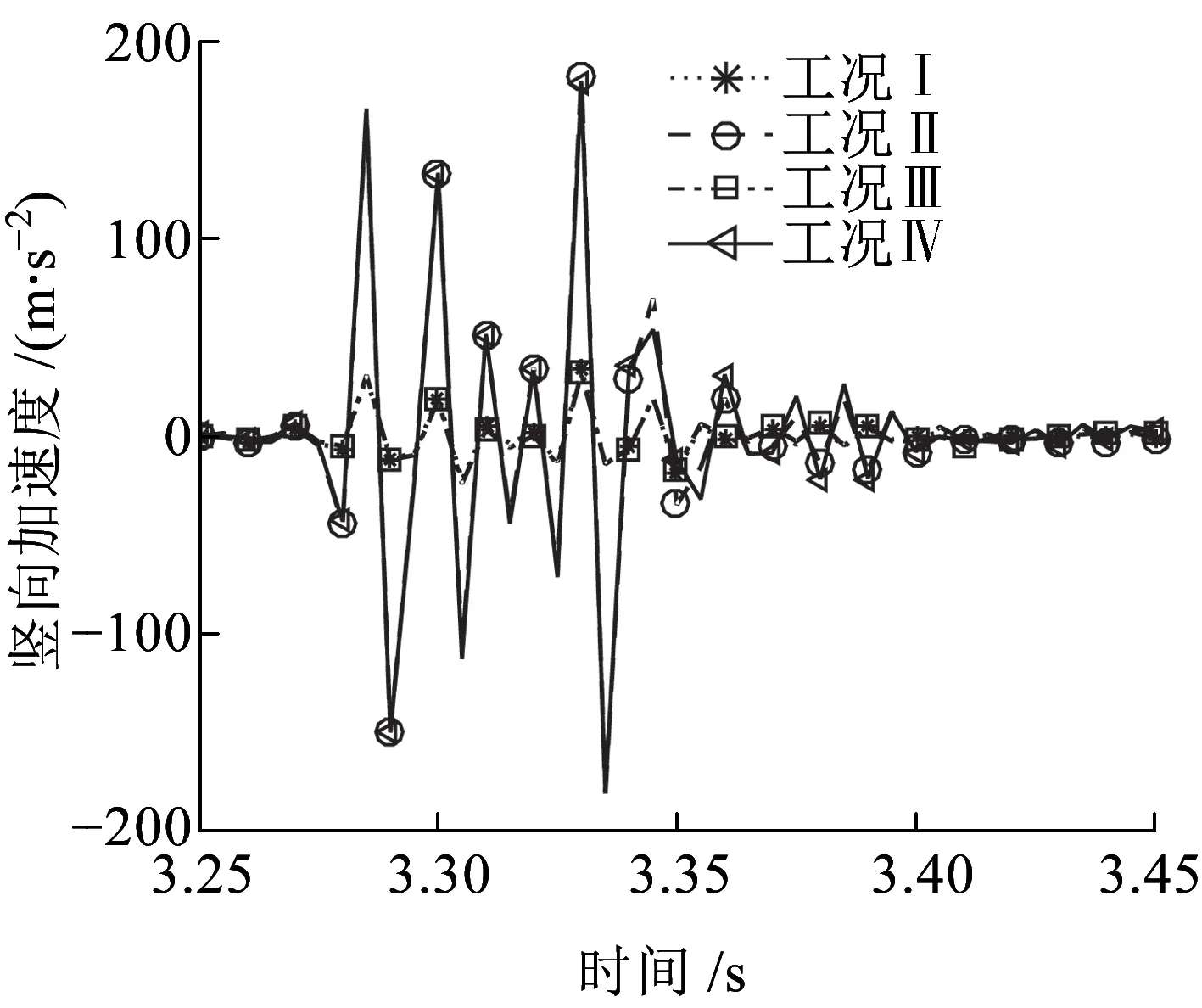
图15 轨道中点A竖向加速度时程曲线

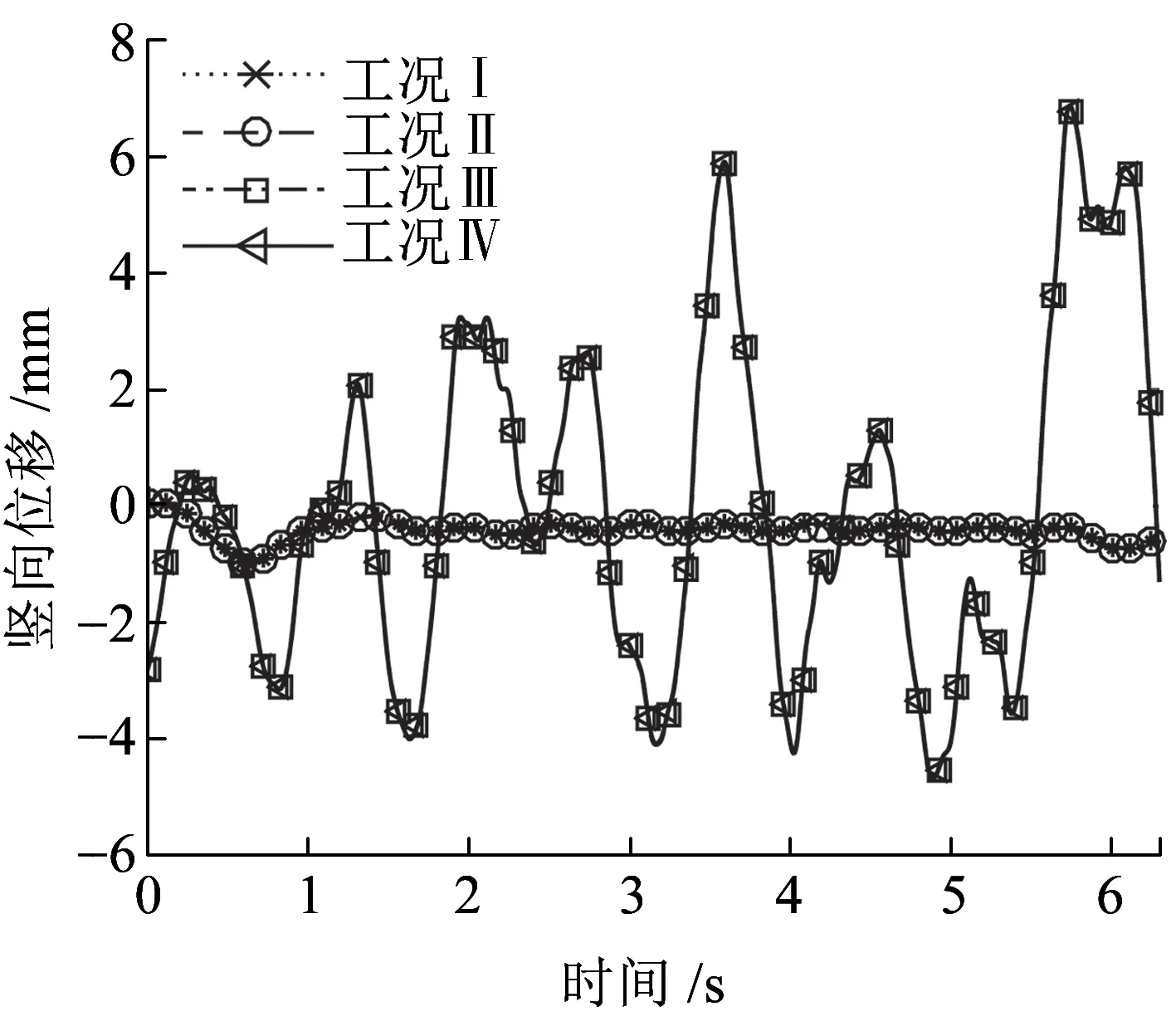
图16 车体质心竖向位移时程曲线

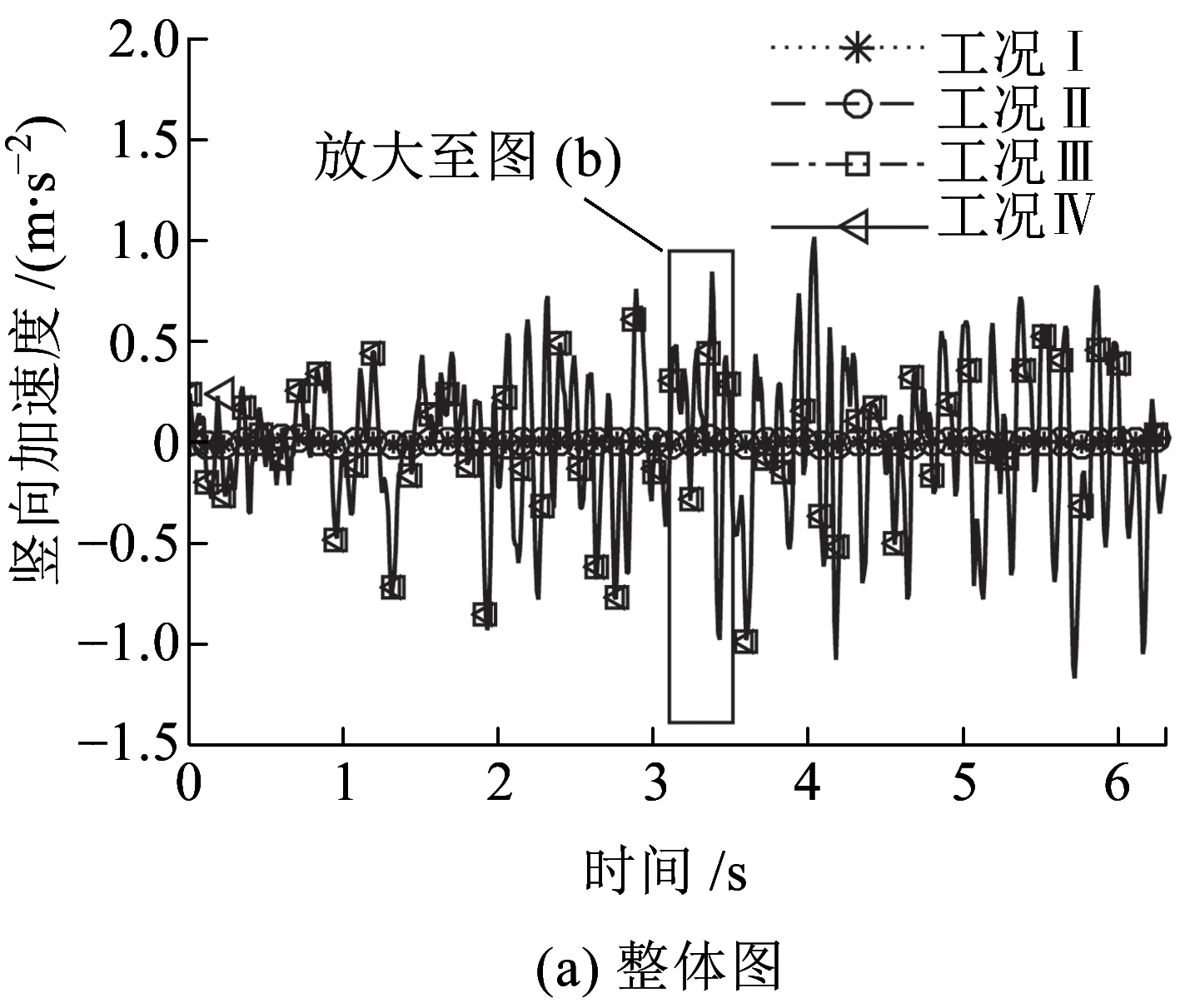
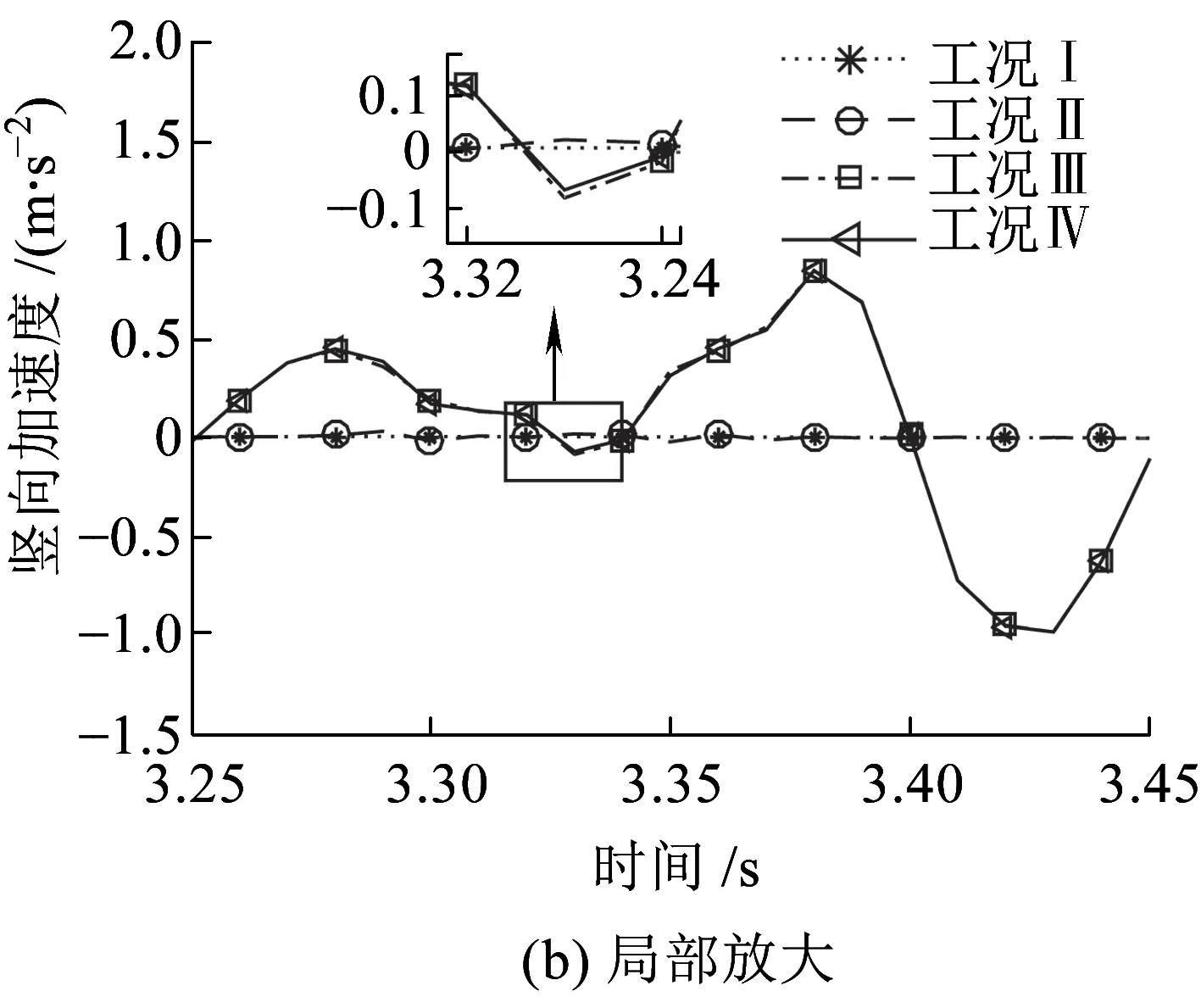
图17 车体质心竖向加速度时程曲线

4 结论

本文提出一种基于非线性接触关系的新型二维轮轨耦合单元。该单元仅考虑轮轨相互作用，单元节点由一个轮节点和列车行进过程中所有可能与之接触的梁单元节点序列组成。通过建立和求解轮轨接触力满足的一元三次方程，得到轮轨之间的接触力，计算由轮轨相互作用产生的耦合单元节点力，最后推导了二维轮轨耦合单元刚度。基于此单元模型，本文建立竖向车桥耦合系统有限元模型并进行地震动力分析。该单元模型有如下优势：(1)易于集成到现有的通用有限元框架，编程难度小；(2)车辆运行中有限元模型无需修改，建模难度小；(3)能够模拟轮轨间非线性接触，可考虑车辆跳轨和轨道不平顺激励的影响。

本文将新型二维轮轨耦合单元模型与列车、轨道和桥梁模型联合使用，分析了竖向车桥系统在轨道不平顺和地震作用同时存在时的动力响应问题，得出如下结论：

(1)地震作用对车体质心竖向位移影响明显，轨道不平顺激励影响较小。地震作用和轨道不平顺激励对车体质心竖向加速度均有影响，但地震作用影响更明显。

(2)与地震作用相比，轨道不平顺激励对竖向轮轨相互作用的影响更明显。

(3)轨道不平顺激励和地震作用对轨道位移影响明显，轨道不平顺激励会改变钢轨位移幅值。轨道不平顺激励对钢轨加速度影响明显，地震作用对其影响较小。

(4)地震作用对桥梁竖向位移影响明显，相反，轨道不平顺激励作用对其影响较小。桥梁竖向加速度对轨道不平顺激励和地震作用都很敏感，轨道不平顺激励会进一步增大加速度幅值。

参考文献：

[1]翟碗明. 车辆-轨道耦合动力学[M]. 4版. 北京：科学出版社，2015.

[2]夏禾，张楠. 车辆与结构动力相互作用[M]. 2版. 北京：科学出版社, 2005.

[3]YANG Y B， YAN J D, WU Y S.Vehicle-bridge Interaction Dynsmics: With Appliactions to High-speed Railways [M]. Singapore: World Scientific Publishing Co., Pte., Ltd., 2004.

[4]林玉森, 李小珍, 强士中. 车桥耦合振动中2种轮轨接触模型的比较分析[J]. 中国铁道科学, 2007, 28(6):70-74.

LIN Yusen, LI Xiaozhen, QIANG Shizhong. Contrast Analysis of Two Wheel-rail Contact Models in the Coupling Vibration of Vehicle-bridge System[J]. China Railway Science, 2007, 28(6):70-74.

[5]YANG Y B, YAU J D. Vehicle-bridge Interaction Element for Dynamic Analysis[J]. Journal of Structural Engineering, 1997, 123(11): 1512-1518.

[6]YANG Y B, CHANG C H, YAU J D. An Element for Analysing Vehicle-bridge Systems Considering Vehicle’s Pitching Effect[J]. International Journal for Numerical Methods in Engineering, 1999,46:1031-1047.

[7]YANG Y B, WU Y S. A Versatile Element for Analyzing Vehicle-bridge Interaction Response[J]. Engineering Structures, 2001, 23(5):452-469.

[8]YANG Y B, WU Y S. Dynamic Stability of Trains Moving over Bridges Shaken by Earthquakes[J]. Journal of Sound and Vibration, 2002, 258(1):65-94.

[9]雷晓燕, 张斌, 刘庆杰. 列车-轨道系统竖向动力分析的车辆轨道单元模型[J]. 振动与冲击, 2010, 29(3): 168-173.

LEI Xiaoyan, ZHANG Bin, LIU Qingjie. Model of Vehicle and Track Elements for Vertical Dynamic Analysis of Vehicle-track System[J].Journal of Vibration and Shock, 2010, 29(3):168-173.

[10]娄平, 曾庆元. 车辆-轨道-桥梁系统竖向运动方程的建立[J]. 铁道学报, 2004, 26(5):71-80.

LOU Ping, ZENG Qingyuan. Formulation of Equations of Vertical Motion for Vehicle-track-bridge System[J]. Journal of the China Railway Society, 2004, 26(5):71-80.

[11]LOU P, ZENG Q Y. Formulation of Equations of Motion of Finite Element Form for Vehicle-track-bridge Interaction System with Two Types of Vehicle Model[J]. International Journal for Numerical Methods in Engineering, 2005, 62(3):435-474.

[12]BOWE C J, MULLARKEY T P. Wheel-rail Contact Elements Incorporating Irregularities[J]. Advances in Engineering Software, 2005, 36(11/12):827-837.

[13]刘常亮, 尹训强, 林皋,等. 基于ANSYS平台的高速列车-轨道-桥梁时变系统地震响应分析[J]. 振动与冲击, 2013, 32(21):58-64.

LIU Changliang，YIN Xunqiang，LIN Gao，et al. Seismic Response Analysis of a Time-varying High Speed Train-rail-bridge System Based on ANSYS[J].Journal of Vibration and Shock, 2013, 32(21):58-64.

[14]MAZZONI S, MCKENNA F, SCOTT M H, et al. Open System for Earthquake Engineering Simulation (OpenSEES) Opensees Command Language Manual[M]. California:University of California, 2006.