考虑视场角约束的捷联导引与控制一体化设计
2018-05-07赵斌,周军
赵 斌,周 军
(西北工业大学精确制导与控制研究所,西安 710072)
0 引 言
目前,战术导弹常采用惯性稳定导引头结合比例导引规律实现精确制导[1]。此类导引头需要高性能的万向支架以实现对目标的稳定跟踪,其造价高、系统复杂。随着制导武器小型化、低成本化的发展,将探测器件与弹体固联安装的一类捷联导引头已成为目前的研究热点[2-3],其能够简化系统结构,提高可靠性并且降低成本。然而,由于探测器光轴不再与弹体运动隔离,因此比例导引所需的角速率信息不再能够直接测量得到,在开展制导控制系统设计时往往需要进行额外的捷联解耦[4-5]。
针对大气层内目标精确打击时,战术导弹通过调整姿态建立攻角以实现法向过载的跟踪。对于全捷联导引体制而言,较大的姿态调整容易导致目标脱离导引头视场,尤其是在末制导阶段,随着弹目相对距离的不断接近,这种潜在问题更加突出[1]。
当前已有学者针对视场角约束下的制导控制问题开展研究,分别基于比例导引[6-8]、最优控制[9-10]、变结构控制[11-12]等给出了解决方案。
在比例导引方法中,文献[6]采用带有时变偏置项的比例导引法实现了制导全过程的视场角约束,其只能用于攻击地面固定目标,并且所引入的制导切换逻辑会引起制导指令跳变,不利于系统工作;文献[7]提出一种采用不同导航比的两阶段真比例导引方法,并解析证明了其可以同时满足视场角约束和终端角约束条件,这种方法同样仅用于攻击静止目标;为了有效应对运动目标,文献[8]设计了一种制导指令同时与视线角速率和视线角成比例的终端角度约束制导律,给出了视场角的近似解析表达式,据此可以选择导引参数以满足视场角约束条件。
最优控制同样被用于解决此问题,文献[9]通过将视场角范围作为不等式约束条件引入最优制导律设计过程中,设计了能够同时满足终端角度和视场角约束的导引律,实现了对静止目标的精确打击;文献[10]基于线性最优控制方法提出了视场角约束导引律,该方法可实现对机动目标的精确打击。
视场角约束是典型的状态约束问题,因此考虑状态约束[11]的变结构控制也被用于解决此问题。文献[12]基于时变滑模和积分型障碍Lyapunov函数设计了新型制导方法,同时满足了视场角约束和攻击角约束,其假设自动驾驶仪理想工作;文献[13]将自动驾驶仪建模为带有有界不确定的一阶惯性环节处理,基于动态面控制结合积分型障碍Lyapunov函数设计了视场角约束制导律,然而其仅适合静止目标。
以上各种方法中视场角都定义为弹体速度方向和弹目视线方向的夹角,其前提是假设导弹飞行攻角近似为零,忽略导弹的姿态运动。而实际大气层内的全捷联导弹主要通过调整弹体姿态建立攻角以实现法向过载的跟踪,在打击运动目标时,攻角为零的假设是不合理的。
捷联导引头的固有属性是测量相对导弹本体的体视线角信息[1],其兼具弹目相对运动与姿态运动信息。因此,为了确保该角度在制导控制过程中始终满足导引头视场角约束,采用导引与控制一体化设计是一种自然而然的方案。
现有导引与控制一体化设计方法[14-18]都没有考虑导引头视场角约束问题,而针对视场角约束问题的研究大都集中于制导律设计[6-12]中。本文以全捷联导弹攻击运动目标为背景,提出了一种考虑捷联视场角约束的导引与控制一体化设计方法。首先,建立了考虑视场角约束的导引与控制一体化设计模型;其次,基于积分型障碍Lyapunov函数[16]结合动态面方法设计了一体化导引控制律,解决了视场角约束问题;针对目标未知机动引起的系统不确定性,采用了一种估计目标机动加速度上界平方的自适应律[19],避免引入符号项,解决了非光滑问题;最终基于Lyapunov稳定理论证明了整个系统的稳定性和有界收敛特性。
1 数学建模
将目标视为质点,考虑导弹的姿态和速度方向,给出纵向平面中弹-目相对运动关系如图1所示。
其中,XOY为惯性坐标系;M,T分别代表导弹和目标;AM,AT分别为导弹与目标的加速度,其方向分别与导弹和目标的速度VM,VT方向垂直;R为弹目相对距离;qL为惯性系视线角;θM,θT分别为导弹与目标的航迹角;Mxb为弹体纵轴方向,由此得到ϑ为弹体俯仰角,qBL为相对弹体系的体视线高低角。
1.1 相关假设
不失一般性,本文在进行捷联导引与控制一体化建模与系统设计时引入如下假设:
假设1. 在短暂的末制导过程中,假设导弹与目标速度大小不变;
假设2. 目标加速度及其微分大小是有界的;
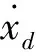
1.2 捷联导引与控制一体化设计建模
根据图1可以建立起考虑体视线约束的捷联导引与控制一体化设计模型,其主要由弹目相对运动模型、弹体姿态控制模型及全捷联导引头解耦模型等三个模型构成。
1) 二维非线性弹目相对运动模型[19]
(1)
对于轴对称战术导弹而言,弹体纵向加速度可以通过气动力系数近似表示如下:
(2)

根据式(1)和(2)可知:
(3)
2) 纵向目平面线性化姿态控制模型[20]
(4)

通常战术导弹的末制导阶段是无动力飞行,即P=0。定义如下模型参数:
由此可对式(4)进行简化:
(5)
3) 全捷联导引头解耦模型
从图1可知,弹体俯仰角、体视线高低角和惯性系视线高低角满足如下关系:
qBL=qL-ϑ
(6)
对其求取微分可得:
(7)
其中,Δqbl=-ωz。
通常稳定飞行的战术导弹,其攻角、舵偏角及角速率都是有界的,并且气动不确定也是有界的,结合假设1和假设2可知:
|Δqbl|≤d1,|Δql|≤d2,|Δα|≤d3,|Δω|≤d4
(8)

(9)
本文的设计目标是设计一体化制导控制规律u,使得系统(9)在不确定性(8)作用下渐进稳定收敛,同时系统体视线角状态满足物理视场角Q的约束:
|x1| (10) 引理1[16]. 定义积分障碍Lyapunov函数(iBLF) (11) 其中,z=x-xd为跟踪误差,|x| 1) 如果状态满足|x| (12) 2) Lyapunov函数V(z,xd)对xd的偏导数如下: (13) (14) 引理3[22]. 对于正数kc,令χ:={x∈R:|x|≤kc,t≥0}与N:=Rl×χ⊂Rl+1均为开集合,考虑系统 V→∞,当|x|→kc时 式中,γ1,γ2均为K∞类函数,令W(η):=V+U(ω)且x(0)∈χ,如果不等式满足 式中,L,D>0,则x∈χ且ω有界。 基于动态面控制,捷联导引与控制一体化设计步骤如下: 1)设计x2的虚拟控制律 定义误差变量s1=x1-x1d,x1d=0,结合式(9)可知微分如下: (15) 以x2作为虚拟控制量,设计x2c为 (16) (17) 为了避免虚拟控制微分膨胀,引入一阶滤波器获取新的变量x2d (18) 2)设计x3的虚拟控制律 定义新的误差变量为s2=x2-x2d,结合式(9)可知微分如下: (19) 以x3作为虚拟控制量,设计x3c为 (20) (21) 同样引入一阶滤波器获取新的变量x3d (22) 3)设计x4的虚拟控制律 定义新的误差变量为s3=x3-x3d,结合式(9)可知微分如下: (23) 以x4作为虚拟控制量,设计x4c为 (24) (25) 同样引入一阶滤波器获取新的变量x4d (26) 4)设计一体化制导控制规律u 定义新的误差变量为s4=x4-x4d,结合式(9)可知微分如下: (27) 由此可以设计控制律u为 (28) (29) 定义推导过程的边界层误差变量为 yi=xid-xic,i=2,3,4 (30) 将式(18)、(22)、(26)代入(30)并结合假设3可知 (31) 根据引理2可知: (32) 定义自适应律的估计偏差如下 (33) 可知估计误差导数为 (34) 根据式(15)和(30)可知: (35) 同理可得: (36) 将式(16)~(29)代入式(35)和式(36),可得: (37) 定理1. 对于捷联导引与控制一体化系统(9),采用控制器(28),如果系统初始体视线角满足|x1(0)| 1)系统4个状态的跟踪误差最终稳定收敛至有界集合内; 2)受限状态x1始终满足体视线约束|x1| 3)闭环系统所有信息均一致有界。 证. 为了确保体视线高低角满足式(10)的约束,设计积分型障Lyapunov函数如下: V=V1+V2+V3+V4 (38) 其中,各个变量定义如下: (39) (40) (41) (42) 根据引理1对式(38)求导可得: (43) 分别将式(31)、(34)和(37)代入上式得到: (44) Δqbls1≤d1|s1|,Δqls2≤d2|s2|Δαs3≤d3|s3|,Δωs4≤d4|s4| (45) 根据引理2可知: (46) 同时还能得到: (47) 将式(45)~(47)代入式(44)可得如下不等式成立: (48) 根据式(12)可知: (49) 选择参数L,D>0,使得: (50) 则可得如下不等式成立: (51) 对式(50)进行积分可得: (52) 1) 对于战术导弹的末制导而言,其目标必然处于导引头视场范围内,因此自然满足|x1(0)| (53) 因此根据式(52)容易得到: (54) 3) 根据结论1~2及引理3可知,系统状态、跟踪误差有界;在此基础上根据式(16)、(20)、(24)和(28)可知所有虚拟控制量及一体化导引控制规律都是有界的,即闭环系统所有信息均一致有界。 注1. 对于红外或激光半主动等导引头而言,通常导引头存在一定的盲区,即当弹目相对距离小于一定数值时导引头输出信息无效,此后导弹通常采用惯性飞行直至命中目标,对于激光半主动导引头而言其盲区实测结果通常约为10~40 m,由此可知式(50)中与相对距离R相关的k2,τ2不存在奇异问题; 注2. 本文使用的自适应律用于对未知干扰上界的平方进行估计(式(17)、(21)、(25)),由此综合得到了光滑的虚拟控制规律(式(16)、(20)、(24))及最终的一体化导引控制规律(式(28))。 以某型捷联导弹为例进行仿真校验,导弹的相关参数如表1所示;算法的相关控制参数见表2。 以正弦机动目标进行仿真验证,目标加速度特性设置为At=20sin(2πt) m/s2。弹目初始的仿真场景设置如表3所示。 表1 导弹参数Table 1 The missile parameters 表2 控制参数Table 2 Parameters used in the control algorithm 表3 初始仿真场景Table 4 Initial Simulation Scenario 选择不同的视场角约束(分别是8°、8.5°和9°),仿真结果如图2~5及表4所示。 表4 仿真结果Table 4 Simulation results 结合图2和表3第二列数据可以看出,在文中设置的场景下,三种视场角约束条件均能满足,因而符合文中定理1的结论2;从图3的局部可以看出,视场角约束越严格,精确打击末端的舵偏角越大,并且所得到的舵偏角光滑并且非奇异,这与式(28)的数学特性相一致;从图4和图5可知,本文所设计的一体化导引与控制系统中的虚拟控制量跟踪误差和动态面设计过程中引入的边界层误差均快速收敛至零附近邻域内,这与定理1的结论3相一致。 为了说明本文方法的优越性,基于传统二次型Lyapunov函数推导了一体化导引与控制律,主要不同点在于式(16)、式(17)和式(39),分别改写如下: (1) 以x2作为虚拟控制量,将x2c改写为 (55) (56) (3) 将第一步的Lyapunov方程改写为 (57) 将本文方法记为iBLF-IGC,传统方法记为QLF-IGC,基于表1 的弹体参数和表2的控制参数进行对比仿真,结果如图6所示。从图中可以看出,在视场角约束为±8°的条件下,传统方法可以实现精确打击,但其实际的体视线角不满足约束条件,而本文所提方法则可以一直保证±8°视场约束。 针对捷联导引体制带来的探测—制导—控制耦合问题,本文结合积分型障碍Lyapunov函数和动态面控制方法提出了一种考虑视场角约束的导引与控制一体化设计方法,通过某激光半主动捷联弹的仿真实例说明了该方法的有效性。 文中设计的自适应律能够实现对目标机动引起的模型不确定性进行自适应估计,在此基础上提出的一体化导引与控制规律能够从理论上保证系统的有界稳定特性,并且满足体视线角状态约束。以上方法对于解决非线性不确定严格反馈系统的状态约束控制问题具有一定的应用价值。 [1] 姚郁, 章国江. 捷联成像制导系统的若干问题探讨[J]. 红外与激光工程, 2006, 35(1): 1-6. [Yao Yu, Zhang Guo-jiang. Discussion on strapdown imaging guidance system [J]. Infrared and Laser Engineering, 2006, 35(1): 1-6.] [2] 孙宝彩, 范军芳. 全捷联小型弹药制导系统设计[J]. 红外与激光工程, 2014, 43(6): 1960-1965. [Sun Bao-cai, Fan Jun-fang. Guidance system design for deeply-strapdown miniature munitions [J]. Infrared and Laser Engineering, 2014, 43(6): 1960-1965.] [3] 温求遒, 李然, 夏群力. 全捷联成像导引头隔离度与寄生回路稳定性研究[J]. 红外与激光工程, 2014, 43(1): 260-266. [Wen Qiu-qiu, Li Ran, Xia Qun-li. Disturbance rejection rate and parasitical loop stability for strapdown imaging seeker [J]. Infrared and Laser Engineering, 2014, 43(1): 260-266.] [4] Sun T T, Chu H R, Zhang B Q, et al. Line-of-sight rate estimation based on UKF for strapdown seeker [J]. Mathematical Problems in Engineering, 2015:185149. [5] 袁亦方, 林德福, 祁载康,等.单兵全捷联图像制导弹药制导信息估计技术[J]. 红外与激光工程, 2015, 44(1): 370-376. [Yuan Yi-fang, Lin De-fu, Qi Zai-kang, et al. Techniques on estimating guidance information for strapdown image guided man portable munitions [J]. Infrared and Laser Engineering, 2015, 44(1): 370-376.] [6] Yang Z, Wang H, Lin D F. Time-varying biased proportional guidance with seeker’s field-of-view limit [J]. International Journal of Aerospace Engineering, 2016: 9272019. [7] Ratnoo A. Analysis of two-stage proportional navigation with heading constraints [J]. Journal of Guidance, Control, and Dynamics, 2016, 39(1): 156-164. [8] Vairavan A, Ratnoo A. A non-switching guidance law for impact angle constrained interception of moving targets [C]. AIAA Guidance, Navigation, and Control Conference, Texas, USA, Jan 9-13, 2017. [9] Park B G, Kim T H, Tahk M J. Optimal impact angle control guidance law considering the seeker’s field-of-view limits [J]. Proc IMechE, Part G: Journal of Aerospace Engineering, 2012, 227(8): 1347-1364. [10] Shaferman V. Optimal guidance with an in route look-angle constraint [C]. AIAA Guidance, Navigation, and Control Conference, Texas, USA, Jan 9-13, 2017. [11] 冯振欣, 郭建国,周军. 高超声速飞行器多约束鲁棒姿态控制器设计[J]. 宇航学报, 2017, 38(8): 839-846. [Feng Zhen-xin, Guo Jian-guo, Zhou Jun. Robust attitude control design for a hypersonic vehicle with multi-constraints [J]. Journal of Astronautics, 2017, 38(8): 839-846.] [12] Wang X L, Zhang Y A, Wu H L. Sliding mode control based impact angle control guidance considering the seeker’s field-of-view constraint [J]. ISA Transactions, 2016, 61: 49-59. [13] Zhang Y A, Wang X L, Wu H L. Impact time control guidance with field-of-view constraint accounting for uncertain system lag [J]. Proc IMechE, Part G: Journal of Aerospace Engineering, 2016, 230(3): 515-529. [14] Hou M Z, Liang X L, Duan G R. Adaptive block dynamic surface control for integrated missile guidance and autopilot [J]. Chinese Journal of Aeronautics, 2013, 26(3): 741-750. [15] Wang X H, Wang J Z. Partial integrated missile guidance and control with finite time convergence [J]. Journal of Guidance, Control and Dynamics, 2013, 36(5): 1399- 1409. [16] Tee K P, Ge S S. Control of state-constrained nonlinear systems using integral barrier Lyapunov functional [C]. 51st IEEE Conference on Decision and Control, Hawaii, USA, Dec 10-13, 2012. [17] 赖超,王卫红,熊少锋. 拦截大机动目标的三维制导控制一体化设计[J]. 宇航学报, 2017, 38(7): 714-722. [Lai Chao, Wang Hong-wei, Xiong Shao-feng. Integrated guidance and control design against highly maneuvering target [J]. Journal of Astronautics, 2017, 38(7): 714-722.] [18] 孙向宇, 晁涛,王松艳,等. 考虑通道耦合因素的制导控制一体化设计方法[J]. 宇航学报, 2016, 37(8): 936-945. [Sun Xiang-yu, Chao Tao, Wang Song-yan, et al. Integrated guidance and control design method considering channel coupling [J]. Journal of Astronautics, 2016, 37(8): 936-945.] [19] Zhao B, Zhou J. Smooth adaptive finite time guidance law with impact angle constraints [J]. International Journal of Aerospace Engineering. 2016, Article ID: 5730168. [20] Hou M Z, Duan G R. Adaptive dynamic surface control for integrated missile guidance and autopilot [J]. International Journal of Automation and Computing, 2011, 8(1): 122-127. [21] Sun C Y, Feng C B. Exponential periodicity and stability of delays neural networks [J]. Mathematics and Computers in Simulation, 2004, 66 (5): 469-478. [22] Tee K P, Ge S S, Tay E H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems [J]. Automatica, 2009, 45 (4): 918-927.2 捷联导引与控制一体化设计
2.1 相关引理
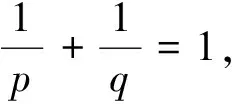

2.2 捷联导引与控制一体化设计
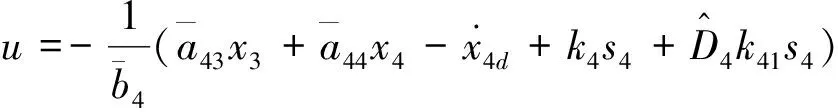
2.3 稳定性分析

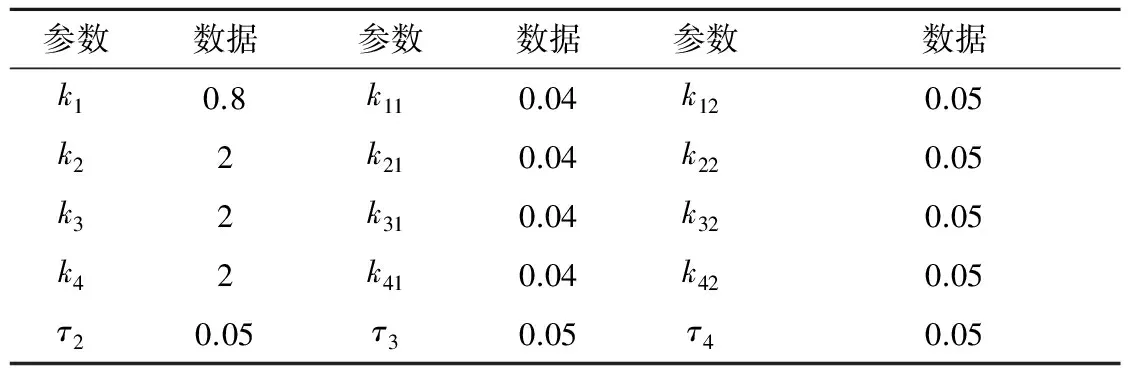
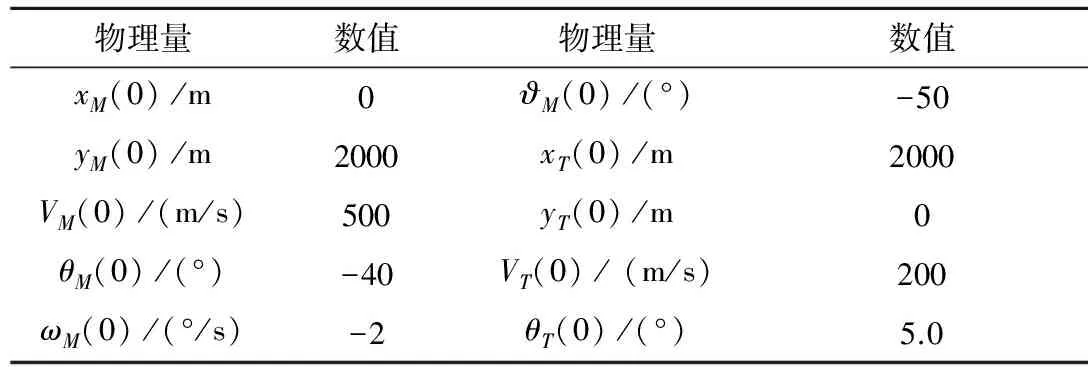
3 仿真校验


4 结 论
