考虑探测构形的多飞行器协同探测与制导一体化设计
2018-05-07王仕成
张 帅,郭 杨,王仕成
(火箭军工程大学精确制导与仿真实验室,西安 710025)
0 引 言
近年来,随着作战模式与航空航天技术的不断发展,拦截器对于目标飞行器已不再具有绝对的机动优势,单一飞行器在对机动目标进行探测和攻击时均存在越发明显的弊端。同时,多飞行器协同作战理念越来越受重视[1]。与传统的一对一拦截方式相比,多飞行器协同在探测和制导方面均具有更大的优势:一方面,多飞行器协同能够对目标状态进行较为全面和准确的探测,弥补单一飞行器对目标动态信息获取的不足[2-3];另一方面,多飞行器协同制导能提高制导精度和拦截概率,进而取得较好的拦截效果。因此,研究多飞行器协同探测和制导问题具有重要的意义[4]。
在多飞行器协同探测方面,双视线协同探测方法可以有效增强拦截方对目标状态信息的估计。文献[5]针对静止目标,基于双视线探测方法提出一种最优拦截制导律,该方法通过引入一个性能指标参量达到调制拦截角大小的目的,但该方法只是定性地描述性能参量与视线分离角之间的关系,不适用于带有预置拦截角度的情况;文献[6]基于双视线探测方法,提出一种三角接近制导律,该方法在保证飞行器自主接近目标时,提高了导航系统对目标状态的观测能力;文献[7-8]针对多拦截器拦截一个机动目标的情况,通过共享视线角信息、施加视线分离角,提出一个新的状态观测方法,增强了对机动目标的状态估计效果。
在协同制导方面,文献[9]针对两个拦截器拦截一个机动目标情况,基于最优控制理论提出一种显示的协同最优制导律;文献[10]基于上述研究成果,考虑多个飞行器协同的情况,将飞行器动力学特性扩展至任意阶,基于最优控制理论推导了合作制导律的一般解析表达形式;文献[11]为增强拦截器之间的通信效果,基于最优控制理论提出一种协同最优制导律,该制导律能够减小拦截器之间相对视角变化,有利于拦截器在饱和攻击时更好地通信;文献[12]针对一对一拦截情况,基于广义分离定理,以末制导系统带宽性能需求为依据,给出一种探测与制导一体化设计方法,该研究初步探讨了探测制导一体化设计思路,是目前国内较早关注探测与制导一体化问题的研究成果。此外,拦截角约束和拦截时间一致性等制导问题也受到了广泛关注,文献[13-14]基于滑模控制理论提出了一种带有终端拦截角约束的制导律;在此基础上,文献[15]针对多飞行器协同拦截机动目标问题,提出一种同时带有拦截角和攻击时间约束的协同制导律。在控制设计方面,文献[16-17]基于鲁棒控制理论对飞行器控制系统稳定性进行了分析;文献[18]针对反舰导弹末段姿态控制问题,将传统的位置跟踪和姿态控制进行统一考虑,提出一种位置和姿态一体化控制方法。
针对探测与制导两个环节,目前的研究主要是基于分离定理进行状态估计器与制导律设计。这些方法通过信息融合和滤波算法设计目标状态估计器以有效估计目标状态信息,将滤波所得的状态信息传递给制导系统形成探测制导闭环回路。但分离定理的核心思想是将探测与制导两个环节分别进行独立设计,该方法在设计制导律时没有充分考虑估计器与制导过程的相互影响,可以看成是基于联合滤波算法的估计器和制导律设计[19-21]。
一直以来,国内外学者大多是将协同探测和协同制导两个环节分开来考虑,在进行制导设计时只考虑目标状态信息的融合和传递,而没有充分考虑到制导过程对协同探测效能的影响,尤其是协同制导几何构形对协同探测效果的影响,也没有形成较为完善的探测制导一体化设计思路。实际上,多飞行器协同探测和协同制导两个环节是相互影响、紧密联系的:协同探测效果将直接影响制导性能,特别是当三个飞行器近似共线时拦截器将无法有效探测到相对距离、速度等信息,这将直接影响拦截器的协同制导效果;另一方面,所设计的制导律在改变飞行器飞行轨迹的同时,也改变了协同探测几何构形,进而影响协同探测效果。不同于上述独立设计的思路,本文统一考虑协同探测与制导两个环节之间的相互影响,从双视线协同探测的原理出发,将协同探测效果对制导环节的影响考虑到系统建模和制导律解算过程中,针对两个环节进行一体化设计。
综上,本文针对多飞行器协同探测与制导两个环节,基于最优控制理论进行了协同探测与制导一体化设计,旨在进一步提高协同探测和制导性能。在制导律设计时通过施加视线分离角参量以调制协同探测几何构形,从而减小相对距离探测误差。同时将协同探测解算的相对距离信息应用到剩余时间估计和制导律解算中,实现了协同探测和制导两个环节的一体化设计。本文所提方法能够在制导过程中使拦截器保持有利的几何探测构形,在制导全程以较小的协同探测误差实现更好的制导效果。
1 问题描述
1.1 动力学与运动学
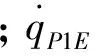
在拦截的过程中,将飞行器加速度沿视线方向和垂直视线方向进行矢量分解,沿视线方向的加速度能够保证拦截器不断接近目标,而垂直视线方向的加速度能够决定视线方向的变化[22-23]。根据惯性坐标系和视线坐标系之间的相互转化关系,忽略视线角速率二阶小量,可以得到拦截器1与目标飞行器在极坐标下二维相对运动[4]:
(1)
同样的,可以得到拦截器2与目标飞行器之间相对运动方程:
(2)
假设在拦截器与目标接近过程中,其各自的机动加速度只改变速度方向,不改变速度大小,则拦截器接近目标的过程可视为常速接近过程。拦截器与目标之间的拦截结束时间可近似为:
(3)
式中,rP1E(0)和rP2E(0)表示初始相对距离,VP1E和VP2E表示接近速度。
假设三个飞行器动力学特性可等效为一阶惯性
环节:
(4)
其中,τ为过载响应时间常数,ac为飞行器控制指令。据此可得飞行控制系统时域描述为:
(5)
1.2 双视线探测模型
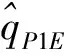
在双机协同的背景下,两个拦截器构成一条测量基准线,可以根据双视线定位原理对目标信息进行更为准确的探测。假设两个拦截器能够进行实时通信且能够相互获取对方状态信息,则在此背景下,可认为两个拦截器之间的相对距离rP1P2和视线角qP1P2是可以被对方精确获得的。据此可以解算出拦截器与目标之间的相对距离:
(6)
(7)
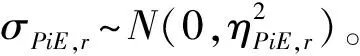
(8)
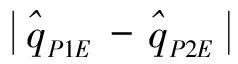
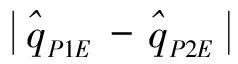
1.3协同拦截模型
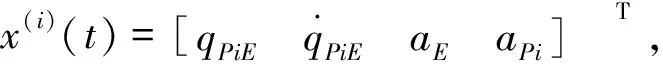
(9)
其中,
式中,ui代表拦截器指令加速度aPiC,为系统控制输入变量,也是需要设计的制导律;aEC为目标飞行器指令加速度,可视为外界输入变量;B(i)和G为相应的传递矩阵。
拦截脱靶量定义为拦截器进入制导盲区时刻的零效脱靶量[23-24],用Z表示拦截脱靶量,可得
(10)
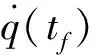
2 协同最优制导律
由于最优控制理论能够保证较小的拦截脱靶量,使系统满足特定的性能需求,如能量最优,且通过终端投影方法求取制导律解析解,因此本节基于最优控制理论进行协同制导律设计[10]。本节将协同制导过程中的探测构形和性能指标约束条件考虑到目标函数中,通过解算拦截器制导律,实现协同探测和制导一体化设计。
2.1 目标函数
在协同拦截过程中,期望以较小的机动代价取得较小的拦截脱靶量。同时根据1.2和1.3节分析可知,为了增强探测效果,拦截过程要始终保证一定的视线分离角,而末段视线角速率决定了拦截脱靶量,因此取目标函数为:
(11)
式中,i=1,2,总的目标函数J由两部分组成,每一部分代表一个拦截器性能指标。tfi表示各拦截器剩余飞行时间。式Ji中,第一项为了保证拦截器具有较小的拦截脱靶量;第二项通过增加视线角约束项以保证一定的视线分离角;第三项为了保证较小的机动能量消耗。
对于上述目标函数,当a1,a2→∞时,可以获得最优制导律;当b1,b2→∞时,可以使视线角最终分别收敛到Δc1,Δc2;当b1,b2→0时,对视线角不施加控制,相应的视线分离角也无控;当c1,c2→∞时,可以使机动能量消耗最小。
2.2 模型降阶
为简化推导过程,求取解析解,需要对式(11)进行模型降阶。这里引入新的状态变量Z(i)(t),i=1,2,令
Z(i)(t)=DΦ(i)(tfi,t)x(i)(t)+
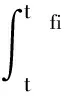
(12)
式中,Φ(i)(tfi,t)为状态方程式所示的状态转移矩阵;D∈R1×4为常值向量,用于分离状态变量x(i)(t)中的元素。
由状态转移矩阵的性质可得:
(13)
可得
DΦ(i)(tfi,t)GaEC=DΦ(i)(tfi,t)B(i)ui
(14)
因此,目标函数Ji可等价变换为:
(15)
2.3 协同最优制导律
以i=1为例,采用最优控制理论求解最优制导律,目标函数的Hamiltonian函数为:
(16)
由横截条件可得:
(17)
由2.2节可知:
(18)
由耦合方程可得最优协同制导律:
可解得:c1u1+λz1d1+λz2d2=0
则最优解为:
(19)
(20)
(21)
其中,

同理可得:
(22)

3 仿真分析
3.1 目标CA机动

从图2所示飞行器运动轨迹可以看出:在初始阶段,由于初始视线分离角较小,本文所提制导律能够增大视线分离角并保持有利的探测构形,而APN制导律只能保证拦截器不断接近目标而不能调制该视线分离角;在拦截末段,当拦截器接近目标飞行器时,此时视线分离角较小,采用APN制导律时,拦截器与目标之间的视线分离角逐渐变小,两个拦截器最终从一侧接近了目标,而本文所提制导律在制导末段同样能够保证拦截器具有较为有利的探测构形。从最终拦截效果来看,采用APN制导律时,拦截器终端脱靶量分别为0.76 m,0.89 m;而拦截器采用本文所提制导律时,终端脱靶量分别为0.56 m,0.49 m。因此,本文所提制导律在整个制导过程中均能够保持有利的探测构形,且具有较高的制导精度。
从图3和图4可以看出,在初始视线分离角相对较小的情况下,本文所提制导律能够保证两个拦截器视线角分别收敛到预定角度,且在此过程中视线分离角始终较大,这可以保证拦截器具有较好的探测效果;而采用APN制导律时,视线分离角在初始视线角速率的影响下逐渐减小,不利于拦截器进行协同探测。图5~6为相对距离探测误差随制导时间变化曲线。从仿真结果可以看出,相比于APN制导律,本文所提制导律能够明显减小探测误差。如图7所示,在目标进行常加速度机动时,本文所提制导律和APN制导律都能够保证视线角速率收敛到0,从而保证拦截器具有较小的拦截脱靶量。
3.2 目标正弦机动
当目标进行更加剧烈的正弦机动时,设目标指令加速度aEC=-70sin(πt)m/s2,拦截角Δc1设为-45°,拦截角Δc2设为45°,其余参数设置与3.1节相同。仿真结果如图8~13所示。
由图8所示飞行器运动轨迹可知,当目标进行更加剧烈的正弦机动时,本文所提制导律也能够保证拦截器在制导全程保持较为有利的探测构形,而APN制导律在协同拦截过程中则不能保证拦截器达到该效果。采用APN制导律时,拦截器终端脱靶量分别为1.26 m,1.08 m;而拦截器采用本文所提制导律时,终端脱靶量分别为0.72 m,0.66 m。仿真结果表明,在目标进行较为剧烈的正弦运动时,本文所提制导律同样能够在制导全程保持较为有利的探测构形,取得较高的制导精度。
图9表明,本文所提制导律能够保证拦截器以预定的视线分离角拦截目标,且在制导过程中始终保持较大的视线分离角;而采用APN制导律时,两个拦截器视线分离角逐渐变小,根据2.2节分析可知,该情况不利于拦截器进行协调探测。由图4和图9可知,本文所提制导律能够较好地应用于不同预置视线分离角的情形,比文献[5]所提方法适用性更广。
由图10~11可知,相比于APN制导律,本文所提探测制导一体化制导方法在目标进行较大幅度机动的情况下也能够有效减小相对探测误差。由于本文所提协同探测制导一体化方法在协同拦截过程中能够保持较为有利的探测构形,使视线分离角始终处于较大的状态,有效地避免了飞行器共线的情况,因而本文所提方法在目标进行大幅机动的情况下也能够保证较小的探测误差。
由图10~12可知,当目标进行更加剧烈的正弦机动时,采用APN制导律时拦截器不能保持较好的拦截队形,导致相对距离探测误差较大,而拦截器对目标机动加速度的估计误差也因此变大。对比图7和12可知,上述情形最终导致拦截器不能很好地跟踪目标,使视线角速率不能收敛到0,协同探测误差最终影响了制导精度;而采用本文一体化协同制导律时,拦截器始终能够有效地跟踪目标,使视线角速率收敛到0。
为检验本文所提协同探测与制导方法的鲁棒性,在本节初始条件和目标机动情况下,开展蒙特卡洛打靶仿真试验。仿真次数设定为N=300次,取两个拦截器拦截脱靶量中的较小值为本次拦截脱靶量,仿真结果如图13所示。
由图13所示的脱靶量分布情况可知,与APN制导律相比,拦截器采用本文所提方法取得的脱靶量平均值更小,且稳定在更小的范围内,表明本文所提方法比APN制导律制导精度更高,且具有较好的鲁棒性。
综上,由于本文采用了协同探测与制导一体化设计方法,在制导过程中拦截器能够保持一定的视线分离角,进而确保了拦截器具有较好的探测几何构形,使拦截器能够取得较小的协同探测和制导误差。上述仿真结果表明,在拦截机动目标时,所提一体化方法具有明显的协同探测和制导优势,且具有较强的鲁棒性。
4 结 论
针对多飞行器协同拦截机动目标过程中的协同探测与制导问题,基于最优控制理论提出了一种考虑探测构形的协同探测与制导一体化制导律。以最小化拦截脱靶量、能量消耗和最大化协同探测效果为目标,通过模型降阶和Hamiltonian函数解算了协同最优制导律,该方法将协同探测效能考虑在建模和制导的过程中,可以应用于预置视线分离角的情况,实现了协同探测与制导一体化设计。仿真结果表明,与APN制导律相比,在目标进行不同程度的机动情况下,所提方法都能够在协同拦截的过程中始终保持较大的视线分离角,有效减小拦截器因共线造成的协同探测误差,实现了有效的制导效果。
[1] 姚郁, 郑天宇, 贺风华等. 飞行器末制导中的几个热点问题与挑战[J]. 航空学报, 2015, 36(8):2696- 2716. [Yao Yu, Zheng Tian-yu, He Feng-hua, et al. Several hot issues and challenges in terminal guidance of flight vehicles [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36 (8): 2696-2716.]
[2] Nardone S C, Lindgren A, and Gong K. Fundamental properties and performance of conventional bearings-only target motion analysis [J]. IEEE Transactions on Automatic Control, 1984, 29(9): 775-787.
[3] Hodgson J. Trajectory optimization using differential inclusion to minimize uncertainty in target location estimation[C]. AIAA Guidance, Navigation, and Control Conference, San Francisco, USA, 2005.
[4] 张鹏. 基于有限时间系统理论的多飞行器协同拦截问题研究[D]. 哈尔滨:哈尔滨工业大学, 2013. [Zhang Peng. Research on cooperative interception using multiple flight vehicles based on finite-time system theory [D]. Harbin: Harbin Institute of Technology, 2013.]
[5] Liu Y F, Qi N M and Shan J J. Cooperative interception with double-line-of-sight-measuring[C]. AIAA Guidance, Navigation, and Control Conference, 2013.
[6] Chen T, Xu S J. Approach guidance with double-line-of-sight-measuring navigation constraint for autonomous rendezvous [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 678-687.
[7] Fonod R, Shima T. Estimation enhancement by cooperatively imposing relative intercept angles [J]. Journal of Guidance, Control, and Dynamics, 2017, 40(7): 1711-1725.
[8] Fonod R, Shima T. Estimation enhancement by imposing a relative intercept angle for defending missiles[C]. AIAA Guidance, Navigation, and Control Conference, Grapevine, USA, 2017.
[9] Shaferman V, Shima T. Cooperative optimal guidance laws for imposing a relative intercept angle [C]. AIAA Guidance, Navigation, and Control Conference, Minnesota, USA, 2012.
[10] Shaferman V, Shima T. Cooperative optimal guidance laws for imposing a relative intercept angle [J]. Journal of Guidance, Control, and Dynamics, 2015, 38(8): 1395-1408.
[11] Balhance N, Weiss M and Shima T. Cooperative guidance law for intrasalvo tracking [J]. Journal of Guidance, Control, and Dynamics, 2017, 40(6): 1441- 1456.
[12] 朱柏羊. 探测制导一体化设计问题研究[D]. 哈尔滨:哈尔滨工业大学, 2015. [Zhu Bai-yang. Research on integrated design of estimation and guidance [D]. Harbin: Harbin Institute of Technology, 2015.]
[13] 孙胜, 张华明, 周荻. 考虑自动驾驶仪动特性的终端角度约束滑模导引律 [J]. 宇航学报, 2013, 34(1): 69-78. [Sun Sheng, Zhang Hua-ming, Zhou Di. Sliding mode guidance law with autopilot lag for terminal angle constrained trajectories [J]. Journal of Astronautics, 2013, 34 (1): 69-78.]
[14] 刁兆师, 单家元. 带末端攻击角约束连续有限时间稳定制导律[J]. 宇航学报, 2014, 35(10): 1141-1149. [Diao Zhao-shi, Shan Jia-yuan. Continuous finite-time stabilization guidance law for terminal impact angle constrained flight trajectory [J]. Journal of Astronautics, 2014, 35 (10): 1141-1149.]
[15] 宋俊红, 宋申民, 徐胜利. 一种拦截机动目标的多导弹协同制导律[J]. 宇航学报, 2016, 37(12): 1306- 1314. [Song Jun-hong, Song Shen-min, Xu Sheng-li. A cooperative guidance law for multiple missiles to intercept maneuvering target [J]. Journal of Astronautics, 2016, 37(12): 1306-1314.]
[16] 王青, 王通, 董朝阳. 切换多胞飞行器的变增益H∞跟踪控制[J].宇航学报,2015, 36(10): 1133-1139. [Wang Qing, Wang Tong, Dong Chao-yang. Variable gainH∞tracking control for switched polytopic vehicle [J]. Journal of Astronautics, 2015, 36(10): 1133-1139.]
[17] 路遥, 王青, 董朝阳. 输出重定义的高超声速飞行器鲁棒自适应控制律设计[J]. 宇航学报,2014, 35(3): 331-339. [Lu Yao, Wang Qing, Dong Chao- yang. A study on output redefinition robust adaptive control method for hypersonic vehicle [J]. Journal of Astronautics, 2014, 35(3): 331-339.]
[18] 吴云洁, 张聪. 主从编队反舰导弹末制导段一体化位姿控制[J]. 宇航学报,2016, 37(12): 1315-1322. [Wu Yun-jie, Zhang Cong. Integrated control of position and attitude for terminal guidance of leader-follower anti-ship missiles [J]. Journal of Astronautics, 2016, 37(12): 1315-1322.]
[19] 叶继坤, 雷虎民, 肖增博等. 基于普通分离原理的制导/估计综合设计方法[J]. 航空学报, 2011, 32(1): 137-143. [Ye Ji-kun, Lei Hu-min, Xiao Zeng-bo, et al. Integration design method of estimation and guidance based on general separation theorem[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1):137-143.]
[20] 李东岩, 张志峰, 王飞等. 基于制导/估计综合设计的协同制导律[J]. 北京理工大学学报, 2012, 32(51): 508-512. [Li Dong-yan, Zhang Zhi-feng, Wang Fei, et al. Cooperative guidance law based on integration design of guidance and estimation [J]. Transactions of Beijing Institute of Technology, 2012, 32(5): 508- 512.]
[21] 樊世杰, 范红旗, 肖怀铁等. 末制导中估计器与制导律设计方法新进展[J]. 自动化学报, 2015, 41(1): 38-46. [Fan Shi-jie, Fan Hong-qi, Xiao Huai-tie, et al. New progress of estimator and guidance law design in terminal guidance [J]. Acta Automatica Sinica, 2015, 41(1): 38-46.]
[22] Guo Y, Yao Y, Wang S C, et al. Maneuver control strategies to maximize prediction errors in ballistic middle phase [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(4): 1225-1234.
[23] Guo Y, Wang S C, Yao Y, et al. Evader maneuver on consideration of energy consumption in flight vehicle interception scenarios [J]. Aerospace Science and Technology, 2011, 15(7): 519-525.
[24] Guo Y, Yao Y, Wang S C, et al. Input output finite-time stabilization of linear systems with finite time boundedness [J]. ISA Transactions, 2014, 53(4): 977- 982.
