多孔材料在整流罩内中高频降噪的应用与优化研究

程修妍，荣吉利，谌相宇，范博超

(1. 北京理工大学宇航学院，北京 100081；2. 中国工程物理研究院电子工程研究所，绵阳 621900)

0 引 言

运载火箭在飞行过程中主要受喷流噪声[1]和气动噪声影响[2]，发射阶段的近场声压级可达170 dB以上[3]。随着运载技术逐步向大直径、少级数、高运载能力发展，整流罩外噪声环境更加恶劣。外部噪声以宽频、随机的形式通过透射和辐射传递到整流罩内部，对内部有效载荷的安全性构成了威胁。因此，降低整流罩内噪声，对保护有效载荷、提高运载火箭水平有着重要意义。

采取降噪措施的首要条件是准确预测整流罩内噪声环境。对于宽频、随机的噪声特点，一般采用有限元方法计算低频噪声，统计能量分析方法计算高频噪声。Pirk等[4]采用了SEA方法研究运载火箭声振模型，并由此开展了噪声控制研究；孙目等[5]应用统计能量方法对某型号导弹的仪器舱进行了高频动力学环境预示，计算结果在300Hz以上与试验较为吻合；张国军[6]建立了某飞行器的SEA模型，通过与试验的对比，说明了SEA方法对振动噪声环境预测的可靠性；朱卫红等[7]采用混合有限元-统计能量分析方法建立航天器声振预示模型，预示了航天器全频段声振环境，通过实验对比验证了预示方法和模型的有效性。

在运载火箭整流罩内通常采用减缓壁面振动和吸收内声场能量两种方式进行降噪处理，中高频噪声主要通过敷设声学覆盖层来吸收能量[8]。多孔材料以其低密度、高孔隙率的优点，有着较好的高频降噪性能；其中，三聚氰胺泡沫、吸音棉等轻质、稳定、耐腐蚀的材料，被应用到整流罩的降噪中。胡迪科等[9]采用FEM、SEA方法对整流罩全频域声振响应进行了分析，并在整流罩内壁增加聚酰亚胺泡沫，提高了整流罩的隔声降噪能力。任方等[10]采用统计能量分析和混响室噪声实验，研究了吸声材料厚度、表面处理及布局方式对整流罩降噪性能影响规律。Lane等[11]通过实验研究了高强度噪声环境下三聚氰胺泡沫在复合材料整流罩内的降噪效果，得出了降噪效果与材料表面覆盖率和质量呈线性关系的结论。NASA对三聚氰胺泡沫进行了一系列的研究，论证了其可行性和效益，深入研究了含三聚氰胺泡沫的多种声学覆盖层吸声特性，并考虑将其用在重型火箭的有效载荷整流罩中[12-13]。

本文基于卫星-整流罩的系统级模型，结合Biot理论和SEA方法，获取多孔材料在整流罩内噪声环境的降噪效果，并分析厚度、敷设率和敷设位置对降噪量的影响，为整流罩内声学覆盖层的设计提供参考。

1 声学覆盖层模型

1.1 多孔材料声传播模型

Biot基于变形势能提出弹性多孔介质中的声传播理论，描述了弹性固体框架和内部流体的相互作用[14]。当声波在多孔材料中传播时，由于空气与固体框架材料的特性阻抗相差较大，声传播引起的框架振动非常小，工程应用中通常忽略框架振动，将其简化为刚性。Johnson-Champoux-Allard模型是较为常用的唯象模型[15]，该模型通过定义与材料微结构几何构型、流体运动和热传导相关的宏观声学参数：孔隙率φ、静态流阻σ、曲率α∞、黏性特征长度Λ和热特征长度Λ′，给出了多孔材料有效密度ρ和压缩模量K的计算公式：

(1)

K(ω)=

(2)

其中，ρ0为空气密度，P0为空气压强，η为空气黏滞系数，γ为空气热容比，Pr为普朗特数，ω为圆频率。JCA模型考虑了多孔介质的黏性惯性效应和热耗散效应，能够较为准确地描述刚性框架多孔材料的吸声特性，其宏观声学参数需通过对微结构的分析和测试来获取。

1.2 多孔材料参数

在多孔材料方面，本文的主要研究对象是密度分别为12 kg/m3和22.5 kg/m3的三聚氰胺泡沫和吸音棉。通过流阻测试、孔隙率测试及Kunt管试验，结合多孔材料声学理论进行数据反演，获得了三聚氰胺泡沫和吸音棉的声学参数，如表 1所示。

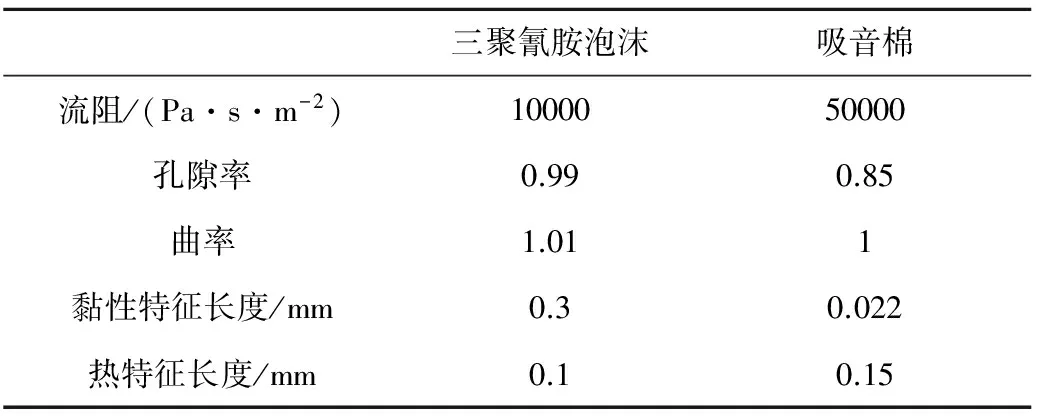
表1 多孔材料声学参数Table 1 Acoustic parameters of porous materials

2 统计能量分析模型

2.1 统计能量分析理论

统计能量分析用统计的观点分析复杂结构在外载作用下的响应，给出空间的和频域的平均量。统计能量分析中，将外部激励作为输入功率，将复杂结构划分为子系统，利用振动能量描述子系统特性，并用能量平衡方程描述子系统间相互作用关系[16]：

(3)

其中，ω为中心频率，E为能量列阵，Pin为输入功率列阵，定义为：

E=[E1,E2,E3,…,EN]T

(4)

Pin=[Pin,1,Pin,2,Pin,3,…,Pin,N]T

(5)

L为系统损耗因子矩阵，包括各个子系统的内损耗因子和子系统间的耦合损耗因子，其数值取决于子系统的自身属性，其矩阵元素为：

(6)

式中ηji为把能量从子系统j传递到子系统i时的耦合损耗因子。对研究对象划分子系统并确定各个子系统的SEA参数后，即可代入式(6)进行系统模型的求解。

2.2 子系统划分及参数设置

卫星-整流罩的系统级模型由外部整流罩和内部卫星结构组成。其外部整流罩由头部(球壳)，前锥段，圆柱段，倒锥段组成，如图 4(a)所示；其内部卫星主要由天线、支架、承力筒、电池阵列等结构组成，如图 4(b)所示。根据模态(振型)相似准则，结合几何自然边界对系统级模型进行子系统划分，各个子系统按照实际尺寸及材料参数建模，模型中共含有结构子系统24个，声腔子系统7个，为研究整流罩的隔声特性及内部声学覆盖层降噪特性，本文主要关注整流罩内部与卫星外部声场，将该声场划分为三个声腔子系统：头部及锥段声腔子系统、圆柱段声腔子系统、倒锥段声腔子系统；此外，为模拟混响室环境，将混响室单独划分为一个声腔子系统。模型的输入功率为混响室声压激励，以能量约束的方式使混响室声腔子系统的声压级与混响室试验测量数据相同。各子系统间根据实际情况分别设置为线连接或面连接。采用LMS SEA+软件进行建模，系统级统计能量分析模型及其连接关系如图 5所示。

部分子系统的SEA参数参考文献[17]进行设置，柱壳结构内损耗因子为0.01；其他未经试验测试的SEA参数,根据参考文献[16]由理论公式计算得出。各声腔子系统和整流罩结构子系统在中低频时的模态数如图6～7所示，在500 Hz以上的频率范围内，声腔子系统和整流罩结构子系统都能满足在分析带宽内模态数大于5 的条件，因此，将该模型的计算频域范围设为500～8000 Hz。

2.3 内声场预示

对图 5所示的SEA模型进行求解计算，得到计算频域内整流罩内部、卫星外部三个声腔子系统的声压级响应，如图 8所示。可以看出，声腔子系统声压级响应趋势与外部混响室激励一致；整流罩在中低频隔声性能较弱，高频隔声性能较好；在8000 Hz处内声腔的声压级有升高的趋势，这是由于频率达到了圆柱段吻合频率。

通过仿真结果与试验数据的对比可以看出，在计算频域内，仿真结果与试验数据吻合较好，头-锥段声腔子系统响应的最大误差为1.38 dB(8000 Hz)，圆柱段声腔子系统响应的最大误差为1.50 dB(1250 Hz)，倒锥段声腔子系统响应的最大误差为1.90 dB(2500 Hz)。仿真误差在2 dB以内，验证了模型的准确性。

由于卫星有效载荷主要集中于整流罩圆柱段，因此对整流罩圆柱段声腔子系统的功率流传递进行分析。图9给出了与圆柱段声腔子系统相连接的各个子系统输入到圆柱段声腔子系统的功率，该子系统的能量输入主要来自于圆柱段和倒锥段声腔，可主要针对这两个部分进行减振降噪处理。

3 多孔材料降噪效果

在系统级模型的整流罩圆柱段内壁上，分别敷设厚度为50 mm的三聚氰胺泡沫和厚度为20 mm的吸音棉，测量了混响室中整流罩内部的声压级，获取了敷设不同降噪材料的降噪性能。

在系统级SEA模型基础上，利用表 1中多孔材料声学参数建立声学覆盖层模型，在LMS SEA+的FOAM模块中利用基于Biot理论的传递矩阵法计算混响室激励下圆柱段声腔子系统的响应，并计算整流罩隔声量。

图11给出了仿真结果和试验数据的对比，可以看出仿真结果与试验较为吻合，两种材料隔声量的仿真结果误差最大值分别为2.56 dB(1600 Hz)、2.43 dB(1250 Hz)，该模型能有效预测多孔材料声学覆盖层的降噪性能。

4 降噪优化

前文通过计算结果与试验数据的对比，验证了计算模型、计算理论的正确性。为达到降噪材料轻量化、降噪效果最大化目标，对声学覆盖层降噪效果影响因素进行分析。

4.1 厚度对降噪效果的影响

分别选取不同厚度的多孔材料铺满整流罩圆柱段内壁，计算不同厚度材料的降噪效果。为与无声学覆盖层的情况进行对比，外部激励仍采用未敷设降噪材料的混响室试验外场测量值。得到敷设三聚氰胺泡沫和吸音棉后圆柱段声腔子系统的声压级如图 12所示；计算可得不同厚度多孔材料的降噪量如图 13所示。

从图中可以看出，敷设不同厚度多孔材料时，圆柱段声腔子系统的响应随频率变化趋势相同；敷设多孔材料后在500～8000 Hz频段范围内，10 mm～70 mm厚度的三聚氰胺泡沫和吸音棉均有一定的降噪效果；两种材料在500-1000 Hz范围内，降噪量随频率的升高而增大，在2000 Hz以上，降噪量随频率升高而略有减小，在1000～2000 Hz范围内，降噪量达到整个频段内的最大值；两种材料的降噪量随厚度的增加而增大，在800 Hz以下，厚度对降噪量的影响较为明显，在高频段内，增加材料厚度对降噪效果没有明显提升。

为评价不同厚度的两种多孔材料在中高频段内的整体降噪效果，计算不同工况下圆柱段声腔子系统的总声压级：

(7)

与无敷设时总声压级对比，获取两种材料的总降噪量与厚度的关系，如图14所示。三聚氰胺泡沫的降噪能力随着厚度的增加而逐渐增强，在厚度大于50 mm时，降噪量随厚度的变化逐渐减缓；吸音棉在30 mm以下降噪能力随厚度增加而增强，在30～50 mm范围内，降噪量随厚度变化幅度较小，在50 mm以上，增加厚度对提高降噪能力并无作用。

采用JCA模型计算不同厚度多孔材料的吸声系数，如图 15所示。三聚氰胺泡沫的吸声系数随着厚度的增加在逐渐增大，其第一共振频率逐渐减小，且峰值逐渐增大；在厚度大于50 mm时，三聚氰胺泡沫的吸声系数在第一共振频率时已趋近于1，此时在中高频段范围内，三聚氰胺泡沫已经能实现较好的降噪性能。吸音棉的吸声系数随厚度的增大而逐渐趋于平稳；其第一共振频率位置随着厚度的增加而逐渐减小，且峰值也逐渐减小；在厚度为60 mm以上时，已没有明显的共振峰；在厚度大于30 mm时，吸音棉的吸声系数较为稳定，波动很小，此时厚度对吸音棉的吸声性能影响较小。

通过分析两种材料在不同厚度时的吸声系数，与图 13、图 14进行对照，可以看出，厚度的增加极大地提升了500-1000 Hz频段的吸声系数，因此两种材料在这一范围内降噪量随厚度的提升较为明显；而高于2000 Hz时，厚度对吸声系数的影响不明显。当厚度大于30 mm时，两种材料吸声系数随厚度变化不明显，这也就导致了其降噪效果随厚度增加并没有明显提升。

综合考虑两种多孔材料的质量和降噪性能，选择50 mm厚的三聚氰胺泡沫为研究对象，进行整流罩内噪声降噪的敷设率优化和位置优化。

根据总体国家安全观，社会安全是国家安全体系中的重要组成内容。预防犯罪是社会安全工作的重要组成部分。我国仍处在刑事犯罪的高发期，违法犯罪活动日趋专业化、职业化，高新技术犯罪增多，对公共安全工作提出了新课题。

4.2 敷设率对降噪效果的影响

采用上述经验证的统计能量分析模型，在整流罩的不同部段内壁均敷设50 mm厚的三聚氰胺泡沫，沿周向改变每个部段的敷设率，求解圆柱段声腔子系统的响应。将所得结果与未敷设多孔材料时进行对比，得到不同敷设率情况下的降噪量，如图 16所示。可以看出，随着敷设率的增加，降噪量增加，但增幅减缓。将降噪量-敷设率数据进行拟合，得到降噪量y随敷设率x变化的二次多项式：

y=-6.1886x2+12.696x+5.1929

(8)

其拟合相关系数R2=0.9724。数据拟合相关系数接近于1，说明拟合多项式能较为准确地表达降噪量与敷设率的关系，可以利用此公式对不同敷设率下的降噪量进行预测，并寻求最优敷设率。

4.3 敷设位置对降噪效果的影响

仍采用上述系统级统计能量分析模型，在整流罩内壁不同位置敷设50 mm厚的三聚氰胺泡沫，并对不同部段的敷设情况进行随机组合。敷设位置及不同工况下的降噪量如表2所示，并计算了不同敷设情况所对应的敷设面积。将敷设面积与降噪量数据绘制于图17，可以看出，当降噪材料敷设在整流罩前半部分，即头部、前锥1、前锥2段时，降噪量数据几乎在拟合曲线下方，即降噪效果低于平均水平；当降噪材料敷设在整流罩中下段，即圆柱段、倒锥时，降噪量数据在拟合曲线上方，即降噪效果高于平均水平；当圆柱段敷设率为50%时，降噪效果高于平均水平最多。由此说明，降噪效果虽然与敷设面积有关，但是，当敷设材料质量有限时，应尽量敷设在整流罩圆柱段及倒锥部分，以达到更好的降噪效果。针对本文中的整流罩模型，可采取沿圆柱段轴向或径向等间隔布局方式敷设降噪材料。结合图9中功率传递情况进行对比可知，该结论与传递路径的分析一致，即当降噪材料质量有限时，应尽量敷设于能量输入较大的部位，从传递路径上降低能量输入，减小内声场声压级。

表2 多孔材料敷设在不同位置的降噪量Table 2 Sound reduction of the porous materials attaching on different positions

5 结 论

本文基于JCA模型研究了三聚氰胺泡沫和吸音棉的吸声特性，仿真、理论计算结果与试验一致，验证了材料参数的正确性；采用SEA方法建立了含卫星的整流罩系统级模型，对无敷设材料和敷设两种多孔材料的混响室试验进行了仿真计算，并通过与试验结果的对比验证了SEA模型和方法的准确性；采用该模型研究了厚度、敷设率和敷设位置对降噪效果的影响。研究结果表明：

(1)将JCA模型和SEA方法相结合，能较为准确地预测多孔材料在整流罩内噪声环境的中高频降噪性能；

(2)三聚氰胺泡沫、吸音棉两种材料均有较好的中高频降噪性能，厚度较低时，随着厚度的增加，降噪性能有所提升，但达到一定程度后降噪性能随厚度的变化不大；

(3)整流罩内总降噪量与敷设率和敷设面积近似呈二次曲线关系，在质量一定时，需考虑整流罩内噪声传递路径，在能量传递较大位置敷设多孔材料，能达到更好的降噪效果。

[1] 刘占卿, 徐悦. 火箭发动机气动噪声辐射特性实验研究[J]. 宇航学报, 2009, 30(4):1606-1614. [Liu Zhan-qing, Xu Yue. Experimental study on radiation characteristics of rocket engine jet noise [J]. Journal of Astronautics, 2009, 30(4):1606-1614.]

[2] 赵瑞, 荣吉利, 任方,等. 火箭整流罩外气动噪声环境的大涡模拟研究[J]. 宇航学报, 2015, 36(9):988-994. [Zhao Rui, Rong Ji-li, Ren Fang, et al. Large eddy simulation of the aeroacoustic environment of a rocket fairing [J]. Journal of Astronautics, 2015, 36(9):988-994.]

[3] 任方, 张正平, 李海波,等. 运载火箭起飞噪声环境缩比模型试验方法[J]. 宇航学报, 2015, 36(3):344-350. [Ren Fang, Zhang Zheng-ping, Li Hai-bo, et al. The lift-off acoustic prediction methods with scale model acoustic test of launch vehicle [J]. Journal of Astronautics, 2015, 36(3):344-350.]

[4] Pirk R, Souto C D. Implementation of acoustic materials to the VLS-1 Fairing - a sensitivity analysis using SEA[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2012, 34(1):82-88.

[5] 孙目, 王小军, 潘忠文,等. 统计能量分析在飞行器动力学环境预示中的应用[J]. 导弹与航天运载技术, 2009(3):11-14. [Sun Mu, Wang Xiao-Jun, Pan Zhong-wen, et al. Applications of statistical energy analysis in prediction of flight dynamics environment [J]. Missiles and Space Vehicles, 2009(3):11-14.]

[6] 张国军, 闫云聚, 李鹏博. 基于统计能量法的飞行器结构声振响应分析[J]. 噪声与振动控制, 2014, 34(3):92-96. [Zhang Guo-jun, Yan Yun-ju, Li Peng-bo. Analysis of vibro-acoustic response of aircrafts based on statistical energy method [J]. Noise and Vibration Control, 2014, 34(3):92-96.]

[7] 朱卫红, 韩增尧, 邹元杰,等. 航天器声振力学环境预示与验证[J]. 宇航学报, 2016, 37(9):1142-1149. [Zhu Wei-hong, Han Zeng-yao, Zou Yuan-jie, et al. Prediction and validation of vibro-acoustic mechanical environment of large complex spacecraft [J]. Journal of Astronautics. 2016, 37(9):1142-1149.]

[8] 荣吉利, 谌相宇, 李彬,等. 圆柱形声腔内衬三聚氰胺泡沫降噪方法[J]. 宇航学报, 2016, 37(10):1271-1278. [Rong Ji-li, Chen Xiang-yu, Li Bin, et al. A method for noise attenuation in cylindrical cavity with melamine foam lining [J]. Journal of Astronautics. 2016, 37(10):1271-1278.]

[9] 胡迪科, 沈林, 柳征勇,等. 新一代运载火箭整流罩全频域声振分析及隔声降噪研究[J]. 上海航天, 2016, 33(b05):29-35. [Hu Di-ke, Shen Lin, Liu Zheng-yong, et al. Vibro-acoustic and noise reduction analysis in full frequency domain of a new launch vehicle fairing [J]. Aerospace Shanghai, 2016, 33(b05):29-35.]

[10] 任方, 张正平, 李海波,等. 基于吸声材料的火箭整流罩噪声环境控制[J]. 固体火箭技术, 2016(06):851-856. [Ren Fang, Zhang Zheng-ping, Li Hai-bo, et al. Noise control technology of launch vehicle fairing using sound-absorbing material [J]. Journal of Solid Rocket Technology, 2016(06):851-856.]

[11] Lane S A, Kennedy S, Richard R. Noise transmission studies of an advanced grid-stiffened composite fairing[J]. Journal of Spacecraft & Rockets, 2012, 44(5):1131-1139.

[12] William O H, Anne M M, Cleveland, O. Acoustic test results of melamine foam with application to payload fairing acoustic attenuation systems [C]. National Conference on Noise Control Engineering, Florida, September, 2014

[13] Anne M M, William O H. Effect of coversheet materials on the acoustic performance of melamine foam [C]. 29th Aerospace Testing Seminar, Los Angeles, October 2015.

[14] Allard J, Atalla N. Propagation of sound in porous media: modelling sound absorbing materials 2e[M]. John Wiley & Sons, 2009..

[15] Allard J, Champoux Y. New empirical equations for sound propagation in rigid frame fibrous materials [J]. Journal of the Acoustical Society of America, 1992, 91(6):3346-3353.

[16] 姚德源. 统计能量分析原理及其应用[M]. 北京:北京理工大学出版社, 1995.

[17] 秦朝红, 任方, 张忠,等. 统计能量分析参数获取技术的应用[J]. 航天器环境工程, 2017, 34(1):8-14.[Qin Zhao-hong, Ren Fang, Zhang Zhong, et al. Application of the method for acquiring SEA parameters [J]. Spacecraft Environment Engineering, 2017, 34(1):8-14.]