既定产教融合模式下学生理想等级结构稳定域分析及其动态调节

宋 平，冯杨杰

（西南财经大学天府学院，四川 绵阳 621000）

产教融合是目前应用型高校人才培养的重要途径。产教融合需要学校教育、产业教育联合培养学生，目前已有很多关于产教融合现状及困难的研究、运行机制研究、支撑系统研究等。不管采用怎样的产教融合培养模式，其作用对象始终是学生，但不同区域、不同高校、不同行业、不同合作产业其产教融合也有区别。因此，很多产教融合的研究及应用经验会因个性差异推广困难。本文将不再进行产教融合前端的模式研究，而将研究重点放到产教融合作用对象学生上，通过分析在既定的产教融合模式下学生在学校教育和产业教育中的结构等级，利用学校专业建设委员会每年对该模式下学生的考核取得各结构等级间的转移比例矩阵，每年通过调入合适的比例，尽快地接近理想等级结构。理想等级结构是由既定产教融合模式下的学校教育和产业教育内部参数确定的（具体解释将在本文推导中解释），即是一旦确定产教融合的模式，其理想的学生等级结构也就确定了。合适稳定的结构对于高校教学、学生成长、产业产出至关重要，比如在既定模式下，学生在校理论学习比例过大，学生动手能力和产业产出会明显不足；在产业从事产业学习的学生比例过大，学生理论知识学习时间不足，既增加产业培养压力，也不利于学生后期发展。在本文中关于这种稳定的研究主要分为两大方面：一是研究哪些等级结构用合适的调入比例可以保持不变，称为调入比例对等级结构的稳定控制，即稳定域分析；二是研究合适的调入比例使结构尽快接近理想等级结构。

一、整体思路

（一）结构等级划分

将既定产教融合人才培养模式下学生等级结构变化状态看作随机系统，根据学生在“高校教育”和“产业教育”中的不同培养阶段划分为三个等级，分别为专业新生、校内成熟学生、产业学习学生。纳入到该种产教融合培养模式下的学生，如果是刚加入的没有基础或基础薄弱的学生称为专业新生；具有一定的专业理论知识，但是实践和动手能力较差的学生称为校内成熟学生；如果是理论知识和实践动手能力齐备，且已进入到产业学习的学生称为产业学习学生。等级结构的评定是由该专业的专业委员会每年通过考试（考核）方式评定。

（二）转移矩阵确定

学生在产教融合中结构等级变化原因主要有两种：一是高校学生内部比例的转移，即能力的提升（或降低，概率非常小）；二是高校学生外部转移，如新生加入和原来学生毕业。将等级结构转移比例看成概率，就可以利用随机转移理论中的马尔科夫链模型相关理论来描述与分析。

等级结构转移比例组成的矩阵称为转移矩阵，其测定方法为：在既定产教融合模式下，通过专业委员会对该模式下学生每年的考评，对各学生等级结构的转移人数进行统计测定，得出转移比例，确定出转移比例矩阵。

（三）各年调入学生比例稳定域分析

由于每年结构等级间有转移，尤其是产业学习学生毕业导致大量人数流失，不利于学生产业学习的成果产出，导致合作企业利益削弱不愿意长期合作。因此，每年应该会有新的各等级结构的人数调入，以期望尽快达到理想等级结构，一旦理想等级结构达到，各等级结构的调入比较将不再变化。但并不是任何等级结构都可以用适当的调入比例使其保持不变，因此需要先求出能够通过调入适当比例保持不变的等级结构的范围，这个过程称为稳定域分析。它可根据系统当前的各种状态和转移比例矩阵，利用马尔科夫链模型，分析计算稳定域。

（四）理想结构的动态调节分析

以稳定域中某点作为理想化目标，分析为达到理想等级结构未来各年学生各等级结构比例以及调入比例，并依此目标作为“产”“教”侧重点动态调整依据。

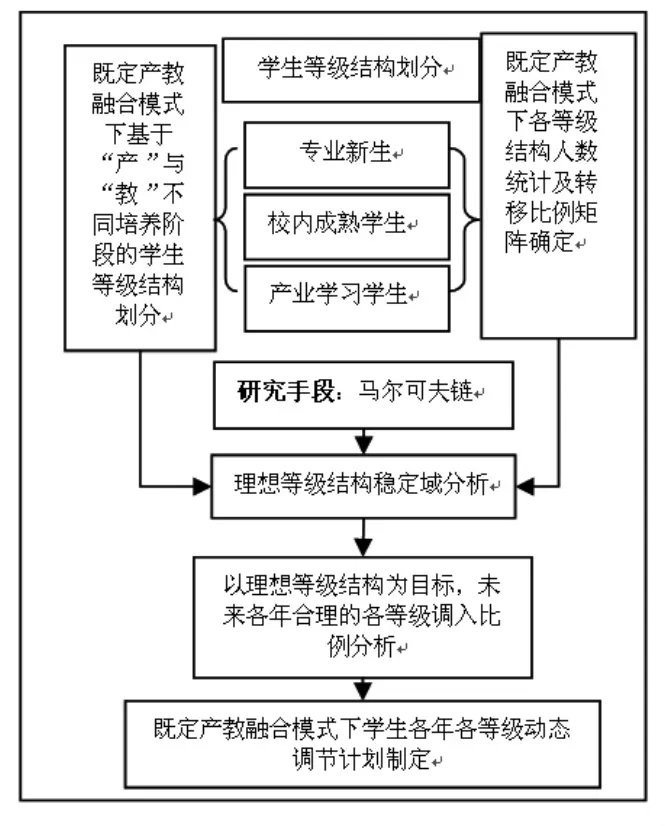
图1 技术路线及内容

二、主要步骤

在高校既定产教融合模式下，专业建设委员会制定学生等级结构划分考核办法，分为三个等级：专业新生、校内成熟学生、产业学习学生。

时间以年为单位，即每年进行一次新的学生结构等级考评，等级记录为 i=1，2，…k，时间记为 t=0，1，2，3……

（一）基本量定义

（a）.记等级为 i=1，2，3（分别对应专业新生、校内成熟学生、产业学习学生）。

（b）.成员按等级的数量分布向量为：

n（t）=[n1（t1），a2（t），...，ak（t）]

其中，n1（t）表示t年属于等级i的人数，t=0，1，2，3表示t年总人数。

（c）.成员按等级的比例分布为：

a（t）=[a1（t），a2（t），…，ak（t）]

a（t）又称为等级结构。

（d）.转移矩阵 Q=[pij]k×k，pij是每年从 i转至 j的比例（在等级i中所占的比例）。

（e）.退出比例向量 w=（w1，w2，w3），wi表示每年从等级i退出系统的成员比例，

表示i年退出系统的总人数。

（f）.调入比例向量 r=（r1，r2，r3），其中 r1为每年调入等级 i的成员比例。R（t）为 t年调入总人数，riR（t）为 t年调入i的人数。

（二）基本模型定义及推导

总人数 N（t）的方程：

记M（t）为从t到t+1年系统总人数的增长量，则：

已知 Q，w，r，M（t），n（t），可预测 n（t+1）

定义：P=Q+wTr

P的行和为1。

当每年系统总人数以固定的百分比增加时，可由成员的等级结构 a（t）代替 n（t）。

如果当 M（t）= αN（t）时，（10）式可变为：

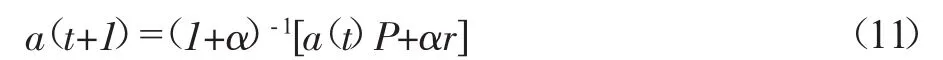
如果每年进出到该产教融合培养模式的学生总数大致相同，即 M（t）=0，则（10）式可以简化为：

上式与马氏链基本方程 a（n+1）=a（n）P 一致。

按此方法可以得出：在既定产教融合模式下的未来学生等级结构理想比例。

（三）用调入比例进行稳定控制

根据之前研究思路的（三），用调入比例进行稳定控制，若存在 r使

称 a=（a1，...ak）为稳定结构。

a≥aQ，a为稳定域。依此稳定域内的数据来制定未来调入比例和学生等级结构规划，也可与未来某年学生等级结构状态对比，动态调整“产”与“教”侧重点。

可以推导稳定域几何上为满足式（14）的点集，下面用矩阵运算进行稳定域构造：

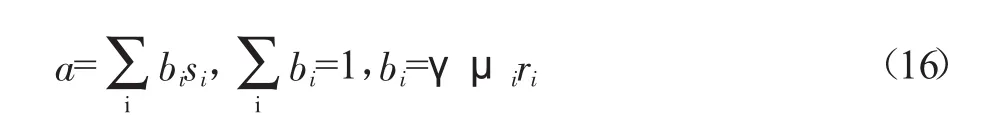
mij≥0，故 μi≥0；γ=awT≥0。

（四）用调入比例进行动态调节

我们现在中心问题是:设理想等级结构为a*，并假定a*属于稳定域B。已知转移矩阵Q和初始等级结构a（0），求调入比例r使得a（1）达到或者尽量接近a*。若没有达到a*时，就要重新调节r逐步使得等级结构比例尽快达到或者尽量接近a*，直到某个时刻a（t）达到了满意程度为止。这个过程我们称为用调入比例对等级结构进行动态调节。

我们用距离来刻划两点之间的接近程度。

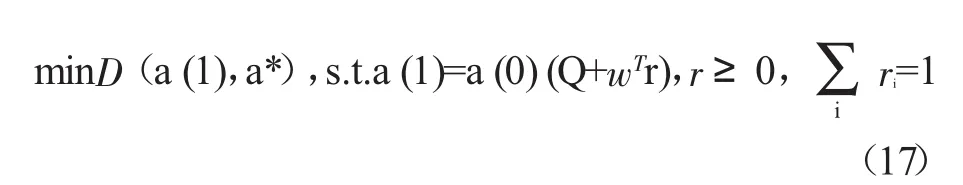
求解过程如下：

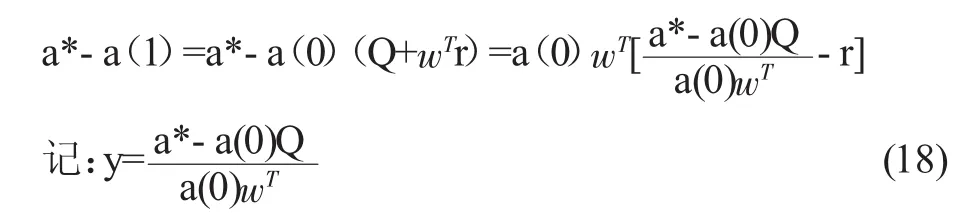
问题推导为求解问题E2

若 y≥0，则解为 r=y，否则将 yi分为 yj＞0（j∈J）和 yi≥0两部分，此时与之对应，我们将r也分为 rj，ri，由于，进一步推导将问题转为求解问题E3

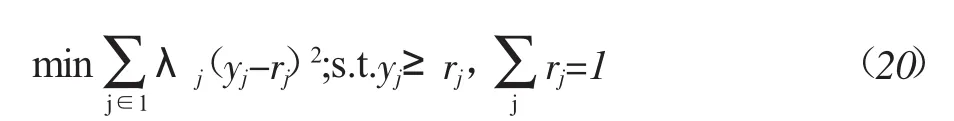
先只考虑后一个等式约束。用Lagrange乘数法我们来求解此条件极值,得到驻点为

其他情况由于在本项目中不用，不作讨论。

三、本校实验项目分析

西南财经大学天府学院与一砖一瓦科技有限公司和西财置业于2014年初联合制定了本校工程造价专业产教融合的人才培养模式，让学生在学校教育和产业教育共同培养下更好地适应川渝地区工程造价人才的需求。由于产教融合模式初步形成，处于探索和不断改进过程中，加上公司和工程诸多硬件条件限制，公司和学校产教融合的原则是：公司现有模式下的硬件设施不盲目增加用以接待更多产业教育学生，学校不完全把所有学生都纳入到该种培养模式中（一方面学校现有其他的学生培养模式，另一方面担心如果该种模式下的产教融合培养效果不理想）。所以，学校和公司一直在寻求在我校现有的工程造价专业既定的产教融合模式下的最理想结构，即产教融合学生在学校教育和产业教育中理想比例分配问题。并且希望根据当年学生结构，分析理想结构稳定域，预估为达到理想结构的各年各等级结构调入比例和调入后各等级结构的组成状态。

本项目的具体实施过程如下：

（一）等级结构划分

以西南财经大学天府学院工程造价专业学生为研究对象，根据既定的产教融合前期合作模式，一砖一瓦公司和西财置业共同制定了本专业该模式下学生培养总人数为每年200人（该专业其他学生用其他人才培养模式培养，允许其他模式学生转入到该种模式），本专业的专业建设委员会为本模式制定等级划分考评办法，并将学生划分为三个等级结构：专业新生、校内成熟学生、产业学习学生。每年设定一次升级考核（考试），考核（考试）对象为全校所有在校工程造价专业有意参加到本模式进行培养的学生。

（二）转移矩阵确定

统计考评结果，列出各等级人数作为统计基数，求出各等级之间转移比例。具体统计数据为：

（a）.2015年第一次考试确定了初始等级人数：（42,128,30）（其中顺序为专业新生、校内成熟学生、产业学习学生，以后类似）。

（b）.2016年第二次考试确定转移人数如下：专业新生等级中，2人考评结果仍然为专业新生，35人通过考评等级结构变为校内成熟学生，2人特别优秀考评结果为产业学习学生且安排进入企业进行产业学习，另有3人主动退出该种培养模式；校内成熟学生等级中，20人考评结果仍然为成熟学生，102人通过考评等级为产业学习学生并被安排进入公司进行产业学习，6人主动退出该种培养模式；产业学习学生等级中学生大多为大三大四学生，大四面临毕业所以退出人数较多，这对企业影响较大，经过考评，合格且没有毕业的产业学习学生为15人，毕业或主动退出为15人。需要声明主动退出该模式的学生其能力培养并不受影响，转入其他模式培养一样成才。

可以得出第一阶段的转移矩阵，由于第一阶段产业学习人数较少，不具备典型意义，所以从第二阶段转移矩阵开始计算，经过第一阶段转移，学生各等级人数为（2,55,119），由于招入新生和其他模式学生主动转入，以第一阶段人数为参考，调入人数统计为（40,60,0）（企业人数已经较多，且调入人数中很少有人能通过第三等级考评因此产业学习学生调入近似为0），本次调入仅为填补空缺，不具备预测规律的作用。调整后的结构等级人数为（42,115,119），上述情况用下图2表示。

用上述方法将2015年考评结果和2016年的考评结果（即等级间转移情况）表述为图3。

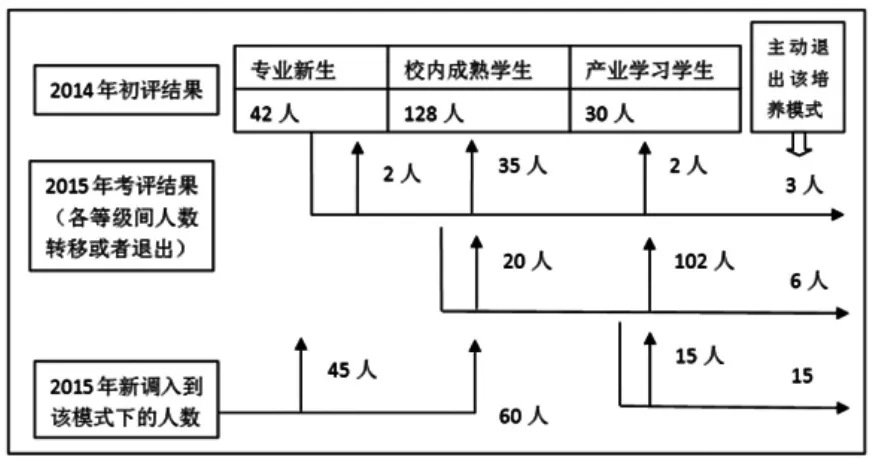
图2 2014年初评结果、2015年考评结果及2015年新调入人数

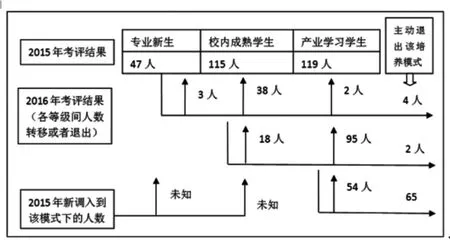
图3 2015年初评结果和2016年考评结果（即等级间转移情况）

由图3得出转移矩阵Q和退出矩阵w：

（三）稳定域分析

由转移矩阵可得由式（15）、（16）可以得：

可以得 S1=（0.287，0.275，0.438），S2=（0，0.398，0.602），S3=（0，0，1）。

其稳定域即为上述三点所围成的三角形区域。

（四）用调入比例进行动态调节

设 a（0）=（0，0，1），理想结构取：a*=（0.287，0.275，0.438）。

现在计算 r使 a（1）接近 a*。设 λi=1-（i=1,2,3），由式（18）可求得 y1=0.526，y2=0.504，y3=-0.029,令 r3，=0 由式（22）求出 a*=0.0147，再求出 r1=0.511，r2=0.489，再由式（21）得出 r=（0.511，0，489，0），由 a（1）=a（0）（Q+wTr）得出a（1）=（0.279,0.267,0.454），这即是一年后达到的最接近a*的等级结构。

用类似的方法，可以求出未来其他各年的适宜调入比例与等级结构，得出结果如下表1所示。

四、结论

通过分析，可以得出如果每年各等级调入人数比例按表1所示，结构等级会越来越趋近于理想等级结构a*=（0.287,0.275,0.438）。我校的产教融合培养模式每年新调入到工程造价专业各等级人数比例也依据表1进行调节，体现的具体效果是一方面学生在校学习有足够的比例，学生有时间进行基础理论知识学习，成熟学生进入到产业学习的人数也恰到好处，没有出现人数过多以致企业不能接纳的程度。且从上表1可以看出，随着该种产教融合模式的延续，虽然学生分为3个等级，但在该种培养模式发展后期，新调入的学生基本都是专业新生。其他等级不能随意加入，不然会影响结构稳定。最明显的问题可能是该种模式的企业现有条件会不满足产业学习学生要求，导致硬件成本增加，引起企业不满，退出该种联合人才培养模式。

不管采用何种产教融合合作模式，一旦模式确定，其理想的高校教育和产业学习学生最适宜的比例也就由其内部参数确定。本文为既定产业融合模式下学生等级结构稳定分析及动态调节提供了参考，且本方法可以避开个性差异具有一定的广泛应用性。

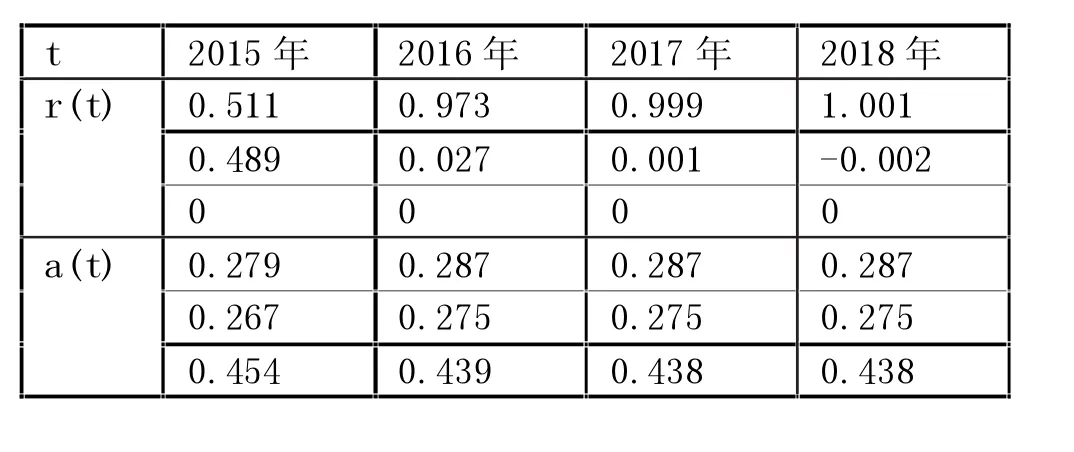
表1 调入比例 r对a（t）的调节

参考文献：

[1]邵甫华.江西高职院校产教融合的困境及对策研究[D].南昌大学，2015.

[2]廖慧琴.广东省高职教育产教融合运行机制研究[D].广东技术师范学院，2016.

[3]刘媛媛.高校转型背景下产教融合支持系统建立研究[D].沈阳师范大学，2016.

[4]刘次华.随机过程[M].武汉:华中科技大学出版社,2001.

[5]李春爱，等.试论齐次马氏链在公共课教师教学评估中的应用[J].洛阳农业高等专科学校学报，1999（3）：46-48

[6]彭梦娇.应用型本科高校产教融合的研究[D].重庆师范大学,2016.