考虑可靠性和舒适性要求的响应式定制公交线路设计

何 民， 李沐轩， 税文兵， 钱慧敏

(昆明理工大学 交通工程学院， 云南 昆明 650500)

0 引言

响应式定制公交是指根据“特定”出行者的需求，在“特定”时间、地点接送乘客出行的一种新型公交运营模式. 由于响应式定制公交的特点是“不定时、不定点、不定车、不定人、不定价”. 因此，响应式定制公交可以为不同出行者提供一种先进的、个性化的和灵活的公共交通服务. 国内外一些开通响应式定制公交的城市的运营经验表明：响应式定制公交系统在其运营过程中比传统的公共交通更具灵活性(如路径、时间等具有更多的选择)，因此可以根据市场特征进行个性化设计，以达到有效控制系统成本或提高服务吸引力的作用[1]. 如美国一些响应式定制公交系统实施成功的城市有[2]：Warsaw，印第安纳州(1995年) 由固定线路的常规公交转为需求响应的公交之后，其运营时长增加，并且实施票价打折后，每日的公交载客量提高了41%，公交运行里程减少了24%；Shakopee，明尼苏达州(1984年)，由固定线路公交转为需求响应公交之后，固定线路公交原来每日载客量为25～50人，变为需求响应公交后，每日载客量为130人，增加了3～5倍.

响应式定制公交吸引乘客的主要因素是其具有较高的可靠性和舒适性. 本文的可靠性是指正常运营的公交系统，在居民可接受出行费用的范围内以及在给定的时间范围内，公交系统把每一位乘客安全、舒适送达目的地的概率[3]. 响应式定制公交的可靠性体现在线路的选择上比常规公交灵活，其不需要按照固定的路线进行行驶，线路阻抗比常规公交的小. 而本文的舒适性指的是出行者对公交提供乘车环境的一种感知度,如果舒适度越高,对出行者的吸引力就越强[4]. 公共交通服务水平的高低、出行者乘坐公共交通的满意度可以由舒适性直接反映[4]. 由于响应式定制公交是1人1座，并且可以根据乘客需求选择不同车型的车，能很好地满足乘客多样化的乘车需求. 因此，本文研究的重点是考虑可靠性和舒适性要求的响应式定制公交线路设计.

响应式定制公交的线路设计与可靠性、舒适性有着密切的关系. 因为，影响响应式定制公交线路的可靠性、舒适性有很多因素：①响应式定制公交线路设计. 若响应式定制公交线路的长度设计过长，那么出行者的出行时间就会增加，可靠性、舒适性就会降低；②响应式定制公交线路的非直线系数. 如果线路的非直线系数过大，那么乘客出行的时间就会增加，行车速度就会降低，可靠性、舒适度就会降低，同时会增加道路通行的拥挤程度；③响应式定制公交线路数量. 因为，线路数量不同，就会有不同的响应式定制公交线路设计；不同的车型选择，就会有不同的载客数量，乘客乘坐不同车型就会有不同的舒适度. 响应式定制公交线路数量越多，那么其在车型的选择方面越灵活，这样在保证可靠性的同时，舒适性也会得到相应的提升. 线路的合理设计对响应式定制公交也有着重要影响. 因此，在响应式定制公交的线路设计上必须要考虑可靠性、舒适性. 因此，本文研究的重点是考虑可靠性和舒适性要求的响应式定制公交线路设计问题.

文献综述从定制公交和常规公交，以及考虑可靠性的车辆路径问题等几方面展开综述. 本文研究的是考虑可靠性和舒适性要求的响应式定制公交线路设计，而定制公交与常规公交中在线路设计都会考虑其运行的可靠性，定制公交是1座1人，对舒适性有所体现；响应式定制公交线路设计和车辆路径问题有着相似之处但又不完全相同；响应式定制公交线路设计与车辆路径问题都是已知需求，并根据客户不同的需求，使用不同车型去完成顾客相应的服务，并设计最短路径. 选择的路径比较灵活，这样就可保证响应式定制公交的可靠性及运营成本. 本文研究的考虑可靠性和舒适性要求的响应式定制公交线路设计的文献综述主要从定制公交和常规公交，以及考虑可靠性车辆路径问题等几方面展开.

Corinne Mulley等[5]阐述了基于固定的网络覆盖范围的灵活公交服务(FTS)，灵活的路线选择以及服务水平是有能力使公交服务恢复活力. Yao baozhen等[6]提出公交网络优化方法，目的是使在优化的公交网络中乘客出行效率最大化，并使用禁忌搜索算法求解该问题的模型. Carlos Carrion等[7]指出出行时间可靠性是出行行为的一个基本因素，它表示出行者在路网中任何2个节点之间的出行经历的时间不确定性，并对当前出行时间的可靠性进行了系统详细的评价.

现有车辆路径问题(VRP)文献的研究从Dantzig and Ramser第一个提出“卡车调度问题”的模型，如何使同类型的卡车车队可以满足从货运中心到加油站卸下石油的最短距离[8]. Naoki Ando等[9]提出车辆路径和调度问题的时间窗概率模型，考虑了出行时间的不确定性，以减少时间和运输成本. X Wang等[10]研究了多车辆路径问题与时间窗(MDVRPTW)问题，并构建了相应的数学模型，提出了一种改进的遗传算法，以反映带有时间窗的多车型多车场的车辆路径问题. H Niu等[11]研究了多车型和多成本的车辆路径问题，考虑不同容量和成本相关的不同车辆类型，并提出了一种适用于遗传算法的启发式算法.

综上所述，通过对定制公交以及车辆路径问题(VRP)的相关文献进一步整理后，得出结论：①现有的大部分“五定”类型的定制公交主要研究了定制公交线路优化、评价等，对定制公交线路优化、线路评价等方面进行了详细研究，并比较了定制公交与其他交通方式的优势以及定制公交线网构建的方法，而对响应式定制公交则以案例研究为主要的研究方向. ②现有车辆路径问题(VRP)可靠性的研究，主要考虑了其行程时间可靠性以及带有时间窗、多车场、多车型等车辆路径问题.

然而，现有的研究还存在以下不足：①对现有的响应式定制公交研究还较少，还缺乏线路优化设计研究；②现有的公交线路设计没有考虑其可靠性、舒适性；③与响应式定制公交线路类似的是车辆路径问题，但是其没有同时考虑可靠性和舒适性.

因此，本文在前人的研究基础上，建立以成本最小为目标的考虑可靠性和舒适性要求的响应式定制公交线路设计模型. 模型中体现了运营商成本最小化以及乘客对响应式定制公交可靠性和舒适性的要求. 为了验证响应式定制公交线路设计模型的正确性和有效性，采用LINGO软件设计一个小规模算例对模型进行求解、验证.

本文研究的响应式定制公交目的在于响应式定制公交作为一种新型的公共交通模式，可以为不同的出行者在不同时间内提供一种舒适、可靠的出行方式. 从而可以满足不同出行者在不同时段、不同地点出行的一种新型公共交通出行方式，进而可以有效缓解道路交通压力，提高居民出行效率. 其意义是响应式定制公交在线路设计上同时考虑了乘客出行的可靠性和舒适性，弥补了现有研究不足之处. 同时，可以为定制公交运营企业在进行线路设计时提供理论指导，帮助运营商更好地吸引乘客.

1 模型的建立

1.1 问题描述

在现实的生活中，对于响应式定制公交线路设计的问题，不能仅考虑路径最短，满足客户需求等单一的目标，而是应该综合考虑许多因素，以达到成本最小化. 研究响应式定制公交线路设计，其主要目的是：在满足顾客要求的服务条件下，把顾客从已知的需求节点安全送到目的地的一种新型出行方式. 响应式定制公交线路设计问题的核心是在以运营成本最小为目标函数的情况下设计一系列响应式定制公交线路以及每条线路的可靠性. 在运行过程中车辆的固定成本是总成本的一部分，不同车型固定成本是不一样的. 因此，在响应式定制公交线路设计中，除了要满足最小的可变成本外，还需要保证不同车型的固定成本最小化.

1.2 模型假设及参数设置

本文针对响应式定制公交线路设计中行驶时间可靠性和舒适性的问题，提出如下的假设：

1)网络中有多个停车场；

2)车辆的起点站和终点站位置都在停车场；

3)各个需求节点可以由几种不同的车型提供，并且不同车型载客能力是有约束的；

4)不同的车型各自都有一条行驶路线，期间可以服务多个需求节点；

5)不同车型的车辆其行驶距离没有限制；

6)各需求节点的上、下车时间都是固定的；

7)不同的车型可根据每个路段行程时间可靠性进行相应的路径选择.

首先需要定义一个完备图G=(V,A)，节点集为V=(1,2,…,n)，定义D为车场点的集合，剩余节点集V′,则是需求点集，其中C为需求点i上不同车型经过同一需求节点的集合(有的节点可以服务不同车型);此外用A={(i,j)|i,j∈V,i≠j}表示弧集或边集.

对于每一条弧(i,j)，定义如下决策变量

1.3 决策模型

根据以上研究构建相应的数学模型，构建的目标函数是车辆出行的可变成本和不同车型的车辆固定成本达到最小; 所构建模型的约束条件如下所示:

(1)

s.t.

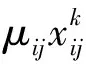
(2)

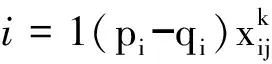
(3)

(4)

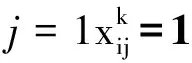
(5)

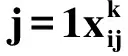
(6)

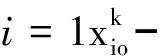
(7)

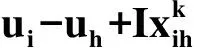
(8)

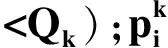
2 算例分析

一般来说，建立的数学模型如果很复杂，那么所描述问题的实际情况就越能够清晰的反映. 为了接近所要描述问题的实际情况，就必须确保构建的模型具有一定的复杂性和适应性. 但是，构建的模型也不能太复杂. 因为如果太复杂，就不能及时发现模型中存在的一些细小错误，算法可能会求解出一个错误的结果，就不能确保模型的正确性. 同时，LINGO软件还会花费很长的运算时间对所构建的模型进行求解，还有可能无法求出其最优解.

响应式定制公交线路设计是一个复杂的问题，因为它涉及乘客、企业以及社会的利益. 并且通过阅读文献后发现，很多学者将研究的重点放在了设计高效的求解算法上，以便可快速准确地对模型进行求解，从而忽略了模型本身的正确性. 因此，本文通过一个小的算例以及模拟的数据对所构建的模型的正确性进行检验，以确保所构的建模型是正确的.

本文准备采用LINGO软件对所构建模型的正确性进行检验，通过检验可以清楚地知道模型的正确性，以及所构建的模型是属于什么类型的数学问题，是线性问题还是非线性问题. 为找到求解模型的算法设计提供思路，以便快速找到适合该模型的求解算法，对以后扩展算例的规模提供帮助.

为了检验构建模型的准确性，本文设计了一个小规模算例来检验该数学模型. 假设该算例有13个需求点,3种车型，在这些需求点中假设需求点1为起始车场，需求点10、11、12、13为终点车场，其余为中间需求点，其中4、5两个需求点可经过两种以上的不同车型. 各需求点之间车辆可变成本如表1所示，模型中使用的各种参数如表2、3所示.

基于上述假设的数据，在8G内存、3.20GHz的酷睿i5处理器上使用版本为LINGO11的软件将上述构建的模型转化为程序语言，同时对所构建的模型设计一个小规模算例进行求解，得到优化方案是：13个需求点中生成了3条路线，详细情况如表4.

分析求解结果可以看出本文建立的考虑可靠性和舒适性要求的响应式定制公交线路设计模型可以正常求解，验证了本文所构建的数学模型的正确性. 从上面所给数据可得出以下结论：在时间相同的情况下，路线3运行车型的固定成本比路线1运行车型的固定成本要高，且座位数比路线1运行的车型要少，得出路线3的车型可靠性比路线1的车型可靠性要高，舒适性也要好. 反之，车型成本较低，座位数较多的情况下，该车型可靠性和舒适性相对较低. 所以，车型的成本不同，可靠性是不同的，舒适性也不同. 固定成本越高的车型，舒适性越好，顾客接受到的服务水平也就越好，可靠性也越高，且可以构成完整线路，表明本文构建模型的正确性.

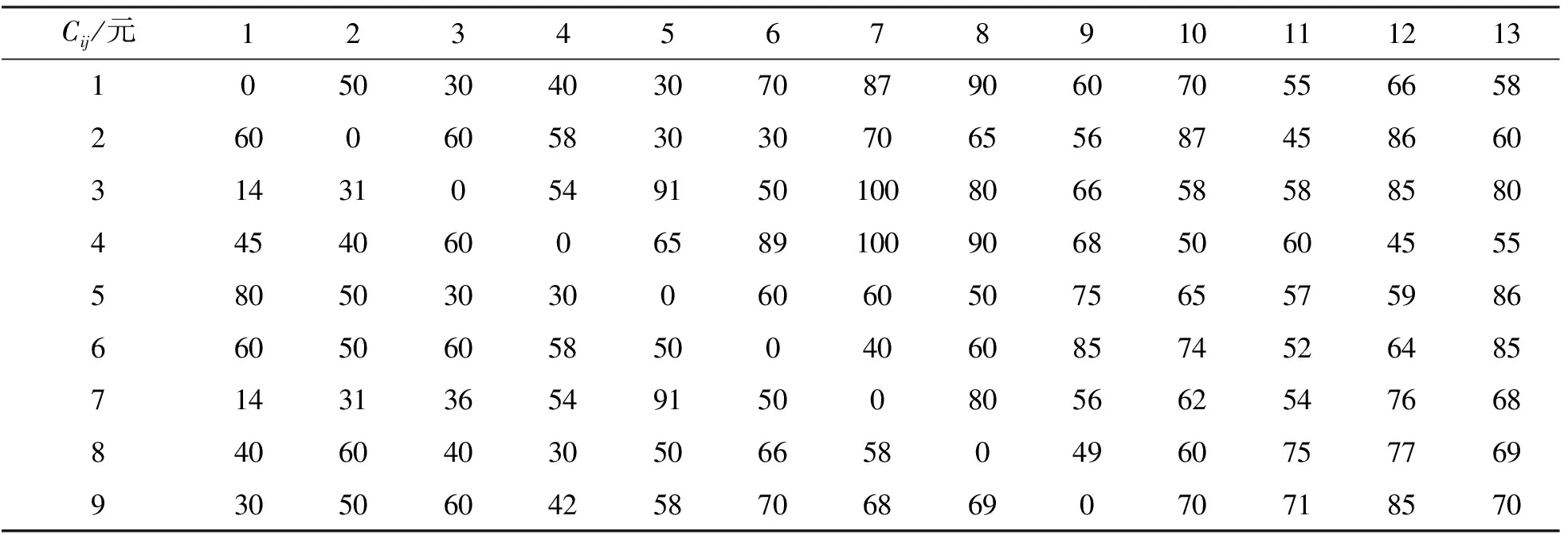
表1 各需求点之间车辆的可变成本

表2 每个需求节点上下车的乘客数

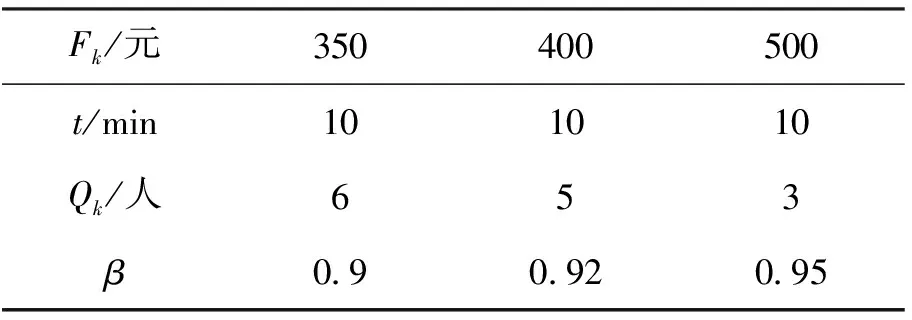
表3 车辆固定成本(Fk)、车辆运行时间(t)、车容量(Qk)，可靠性相关参数(β)

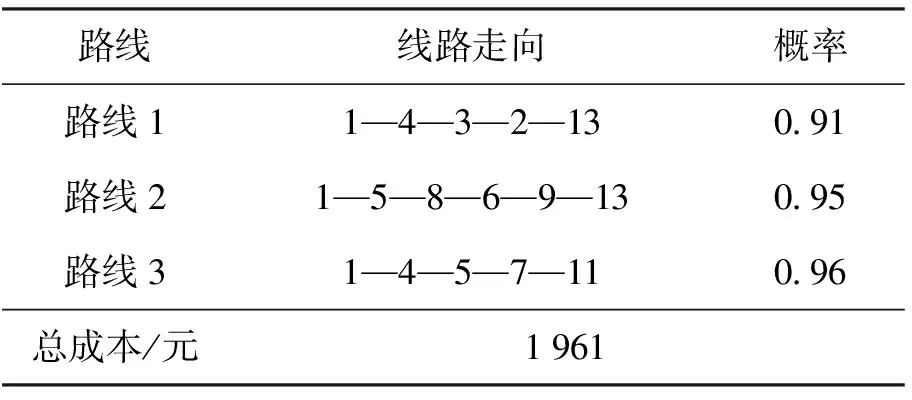
表4 定制公交线路生成情况

3 结束语

响应式定制公交能满足不同出行者的多样化出行需求，其具有一站式到达、舒适的乘车环境等特征而受到乘客的喜爱. 研究响应式定制公交线路设计问题，对于改善城市公共交通服务和缓解城市交通拥堵具有重要意义. 本文从可靠性和舒适性2方面着手研究响应式定制公交的线路设计，探究合理的决策模型来设计合理的响应式定制公交线路. 基于运营成本最低原则并结合可靠性和舒适性要求，建立了响应式定制公交线路设计的数学模型. 通过乘客的不同出行需求设计一个小规模算例，并运用LINGO软件对所构建的数学模型进行求解，得出了相应的线路，算出了最终的成本. 得出了不同成本的不同车型其可靠性和舒适性不同的结论. 根据lingo软件对该模型求解得出的结果表明：固定成本越高的车型，运营商所能提供的服务水平就越好，可靠性也越高，这证实了算法的有效性和正确性. 本文研究的考虑可靠性和舒适性要求的响应式定制公交线路设计在现实应用中具有指导作用，对推动当代城市公共交通健康发展具有一定的实际意义.

参考文献：

[1] 沈昱, 关函非. 响应需求公交系统分析与实施要点研究[J]. 交通与运输: 学术版, 2010(H12): 75-78.

[2] Richard H. Pratt, GarrettPark. Traveler Response to Transportation System Changes Interim Handbook, chapter 6. Demand Responsive/ADA[R]. Transit Cooperative Research Program, March, 2000.

[3] 柳波, 余红红. 基于可靠性的快速公交线路评价体系[J]. 交通科学与工程, 2012, 28(3): 90-94.

[4] 席姣姣. 常规公交服务水平指标体系与评价方法研究[D]. 长春: 吉林大学, 2013.

[5] Mulley C, Nelson J, Teal R, et al. Barriers to implementing flexible transport services: An international comparison of the experiences in Australia, Europe and USA[J]. Research in Transportation Business & Management, 2012, 3(2): 3-11.

[6] Yao B, Hu P, Lu X, et al. Transit network design based on travel time reliability[J]. Transportation Research Part C Emerging Technologies, 2014, 43: 233-248.

[7] Carrion C, Levinson D. Value of travel time reliability: a review of current evidence[J]. Transportation Research Part A Policy & Practice, 2012, 46(4): 720-741.

[8] Dantzig G B, Ramser J H. The truck dispatching problem[J]. Management Science, 1959, 6(1): 80-91.

[9] Ando N, Taniguchi E. Travel time reliability in vehicle routing and scheduling with time windows[J]. Networks and Spatial Economics, 2006, 6(3): 293-311.

[10] Wang X, Xu C, Shang H. Multi-depot vehicle routing problem with time Windows and multi-type vehicle number limits and its genetic algorithm[C]∥International Conference on Wireless Communications, NETWORKING and Mobile Computing, 2008: 1-5.

[11] Niu H, Tao Y, Yang Y. A genetic algorithm for the vehicle routing problem with multi-type and multi-cost[C]∥International Conference on Intelligent System and Knowledge Engineering. IEEE, 2008: 497-501.