基于OP模型的高速公路交通事故人员伤害程度分析方法

刘 博， 杨 静， 朱经纬， 刘 侃

(北京建筑大学 土木与交通工程学院， 北京 100044)

0 背景

随着我国社会经济的快速发展，高速公路的建设取得了长足进步，极大地提高了我国公路网的服务水平. 但高速公路易发生重特大事故，重伤、死亡率高的问题，同样困扰着高速公路的管理者和使用者. 研究公路交通事故伤害程度的影响因素，有助于解析交通事故发生的内因以及通过针对性的措施降低事故伤害，是公路交通安全需要研究的重要内容[1].

国内外对交通事故等级的确定均以人员的伤亡情况为重要依据，目前已有大量成果研究多种客观交通因素对人受伤情况的影响. 国外对道路交通事故伤害程度影响因素的研究起步较早，已有成果多使用警方的事故报告数据，关注事故在特定情况下的发生率以及交通参与者的受伤程度. Celik, Ali Kemal等[1]利用有序响应模型与无序响应模型分析了特定地区的交通事故统计，以描述潜在危险因素对交通事故伤害程度的影响，结果显示许多因素都会对事故伤害严重程度有影响，如驾驶员、事故车辆、事故时段等. Rovšek等[2]将事故统计数据分为3个子集并构建非参数分类树，应用分类和递归树算法确定对事故及伤害的程度有着影响最显著的因素，最后采用重要度量度方法计算9种因素对目标函数的影响. 我国的马壮林等[3]利用Logistic回归模型对公路隧道交通事故进行分析，阐述了时间、隧道环境和交通动态等因素对事故严重程度之间的影响. 目前，仍有较多研究采用logit/probit及其变形模型进行数据分析[4-7].

但这些成果对选用特定因素进行事故伤害程度影响分析的原因有欠论证，较少对多种、具有一定相关性的复杂影响因素的综合分析. 考虑因素较少，难以对外界因素进行完整的描述，但交通事故的客观因素错综复杂，可能存在相互影响，若全部纳入分析会导致结果难于分析，不利于实践. 针对以上问题，提出了相对完整的高速公路交通事故伤害程度影响因素选取及分析方法，并通过实例进行阐述，确定易导致人员受伤加重的影响因素，为制定能够降低伤者受伤程度的措施提供指导.

1 交通事故伤害程度影响因素分析

公路系统是一个由人、车、路、环境构成的复杂系统，任何不利因素都可能导致事故伤害加重. 而交通事故处理工作需要对责任进行划分，因此常将事故原因归为交通参与者的主观因素，如注意力不集中等，却忽视了客观因素在交通事故中的影响[8]. 但客观因素会对伤者的受伤程度产生影响，如已有大量研究证明使用安全带可以显著降低死亡率.

由于考量的因素多维且可能存在相互交织，对伤害程度的影响不能直观地展示，因此利用数学分析方法进行阐述：以高速公路事故统计为基础，以事故伤害程度为因变量，从包含人、车、路、环境的信息中初步选取16种可能影响事故伤害程度的客观因素作为自变量，这16种因素尽可能完整地描述了客观条件，包括：人的因素，如年龄、性别、是否饮酒；车辆因素，如车型、车内人数、车辆翻转情况、安全气囊弹出情况、安全带使用情况；环境因素，如光照条件、天气、发生时刻、发生月份；道路因素，如事故发生地路面情况、是否在工作区、事故发生地车道数、速度限制等等. 利用主成分分析法对以上因素进行主要自变量筛选，之后采用Ordered Probit模型分析各影响因素对交通事故伤害程度的影响. 数据分析结果显示，安全气囊、车型和速度限制对事故伤害程度影响显著.

2 模型构建与检验

2.1 影响因素降维处理

交通事故分析包含了很多客观因素，以尽可能完整地描述客观环境，但过多的因素导致计算量增大，分析过程更为复杂，结果也难以展示. 因此首先利用主成分分析法对初选影响因素进行降维处理，以提取能够反映整体客观环境的综合指标.

主成分分析法(Principal Component Analysis，PCA)是一种高效的降维方法，该方法把多个具有一定相关性的指标约化为少数几个综合指标，被广泛应用于指标合成[9]. 该方法的目标是在尽可能多地保留原始信息的前提下，简化指标维度，而最终主成分(principal component)个数的多少，将使其对原始指标或变量的解释程度产生影响. 整体来说，较多的主成分可以更好地反映原始变量，但也会在一定程度上增加计算量.

初步选取了16种因素作为原始变量，用向量表示为X=(X1,X2,…,Xp)，其中p=16.Xi=(x1i,x2i,…,xni)′，xni代表第n场事故的第i种(i=1，2，…，p)因素. 根据主成分分析的方法，第i个主成分可以表示为：

Pi=a1iX1+a2iX2+…+apiXp

(5)

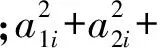
在进行主成分分析时，可以使用相关系数矩阵(R)或者协方差矩阵(Σ)，二者各有优缺点，而使用不同的方法，主成分线性表达式中Xi(i=1,2，…，16)的含义也有所区别. 如果使用相关系数矩阵进行主成分分析，则Xi等同于均值调整后的数据除以标准差，是经过正态标准化的数据；若使用协方差矩阵，则Xi指的是均值调整(mean-corrected)后的数据. 在使用协方差矩阵时，常常需要采用一定的技术对原始指标进行标准化从而消除量纲不同所带来的负面影响，需要注意，如果进行了正态标准化后再使用协方差矩阵，等同于直接使用相关系数矩阵.

2.2 基于Ordered Probit的分析模型构建

在对初选因素进行降维处理后，就可以进一步分析各因素与事故所造成的伤害程度间的影响关系. 研究内容中的自变量为多项有序的离散变量，Ordered Probit (OP)模型是用来分析有序离散变量的常用方法之一，本研究采用该方法可取得较好的分析结果.

OP模型使用了潜变量分析各种伤害程度，潜变量表达式如式(1)～(3)所示.

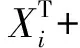
(1)

Xi={1,xi1,…，xij，…，xim}T

(2)

β={β0,β1,…,βj，…，βm}T

(3)

式中，zi为第i场事故的潜变量，Xi为第i场事故的自变量，xij为第i场事故中的第j个自变量，i=1，2，…，n，n为事故的总数，j=1，…，m，m为自变量的总数，β为该自变量系数的列向量；εi为服从正态分布的随机误差项.

因变量yi的表达式如式(4)～(6)所示.

(4)

γ={γ0,γ1,…,γC}

(5)

-∞=γ0≤γ1≤…≤γk≤…≤γC-1≤γC=+∞

(6)

式中，γC为不同事故伤害程度的阀值，C=4.

当得到Xi的值，第i场事故的伤害程度的概率如式(7)所示.

(7)

式中，Piy为第i场事故伤害程度为y的概率；φ()为服从正态分布的累计概率函数.

2.3 模型检验

主成分分析法在自变量筛选的过程中，已经进行了回归系数的显著性检验，因此进行似然比检验和拟合优度检验足以判定模型的准确性.

1) 似然比检验

似然比检验首先进行全部解释变量的系数都为0的原假设，其统计量LR为：

LR=2(lnL-lnL0)

(8)

式中，lnL为对概率模型进行最大似然估计的对数似然函数值，lnL0为估计只有截距项的模型的对数似然函数值. 当原假设成立时，LR的渐近分布是自由度为k-1(即除截距项外的解释变量的个数)的χ2分布.

2) 皮尔逊χ2拟合优度检验

皮尔逊χ2检验可以通过比较实际事故统计与模型预测事故发生与否的情况差别来检验模型的拟合优度[10]，其计算式为：

(9)

式中，n为协变类型的种类数；fi为第i类协变类型中的观测频数；ei为第i类协变类型中的预测频数.

皮尔逊χ2统计量的值越大，表示模型的预测值和实际观测值差别越显著，说明了模型的拟合效果不佳；反之，说明模型的拟合效果越好.

3 实例研究

由于我国交通事故统计数据难以获取，因此使用了美国高速公路交通事故数据统计[11]为研究对象，分析2012年发生的2 264起高速公路交通事故，以验证方法的有效性. 下文将使用主成分分析法提取主要变量，利用OP模型建立主要变量对交通事故伤害影响程度分析模型，最后进行模型检验.

3.1 影响因素初选及预处理

将事故分为5个等级，0代表无人员伤亡的财产损失事故，随数字增大事故伤害逐渐加重，4代表有人死亡的重大事故.

事故数据统计了交通事故的众多因素，包括了人、车、路以及环境的各种特征，如事故中人的年龄，车的类型，事故地段有几条车道，事故发生的时间及当时的天气状况等. 由于属性过多会导致分析结果非常复杂，难以观察，因此在所有因素中初步筛选了16种通常认为与事故程度和事故率相关性较高的因素进行分析，为了分析定性因素，将定性因素转化为数值型并引用哑变量. 因素数据预处理方法如下：

1)年龄：为定量变量，指交通参与者在受伤时的年龄，根据他们上一次生日确定，统计范围为0岁至111岁.

2)性别：为定性变量，男性取0，女性取1.

3)安全带使用情况：为定性变量，分为使用和未使用2类，若伤者使用了安全带则值取0，若未使用则取1.

4)安全气囊弹出：为定性变量，分为弹出和未弹出2类，若未弹出则值取0，弹出则取1.

5)碰撞类型：为定性变量，分为未与车辆碰撞、正面碰撞和侧面碰撞3类，若未碰撞则值取0，正碰取1，侧碰取2.

6)光照条件：为定性变量，分为白天、无光的夜晚、有光的夜晚和其它视线受影响情况4类，将白天定为0，无光的夜晚为1，有光的夜晚为2，其他情况为3.

7)路段限速：为定性变量，分为3种情况，路段限速为40 mile/h以下则值取0，40 mile/h以上60 mile/h以下为1，60 mile/h以上80 mile/h以下为2.

8)车辆类型：为定性变量，包括小轿车、小型卡车、大型卡车、大型客车等8类，将小轿车的值设为0.

9)工作区：为定性变量，分为非工作区、在建、维修中、多种用途土地和其它工作区5类，依次对应数值0至4.

10)天气：为定性变量，分为晴朗、雨、雨夹雪、雪、雾、强侧风、扬沙、多云、飞雪和其它类型，依次对应数值0至9.

11)事故发生小时：为定量变量，为第一事故发生的具体时刻，数值为1～24的整数.

12)月份：为定量变量，为第一事故发生的具体月份，数值为1～12的整数.

13)车内人数：为定量变量，解释发生事故时车内的人数.

14)车辆翻转：为定性变量，解释了车辆是否发生翻转或倾覆，根据多种情况分为9类，对应数值0～8.

15)是否饮酒：为定性变量，如果该伤者未饮酒则值为0，饮酒为1.

16)路面情况：为定性变量，反映了事故发生地的路面情况，共有无道路、道路干燥、湿滑、积雪、结冰、积沙等12种情况，对应数值0～11.

3.2 主因变量筛选

利用主成分分析法对以上16种因素提取主成分，得到表1中结果. 观察可知，主成分1、2、3的方差累计贡献率为85.39%，满足PCA的一般要求，认为这3种主成分可以充分反映所有初选因素. 因此，年龄、安全气囊弹出、车型和速度限制4种因素可以代表所有其他因素.

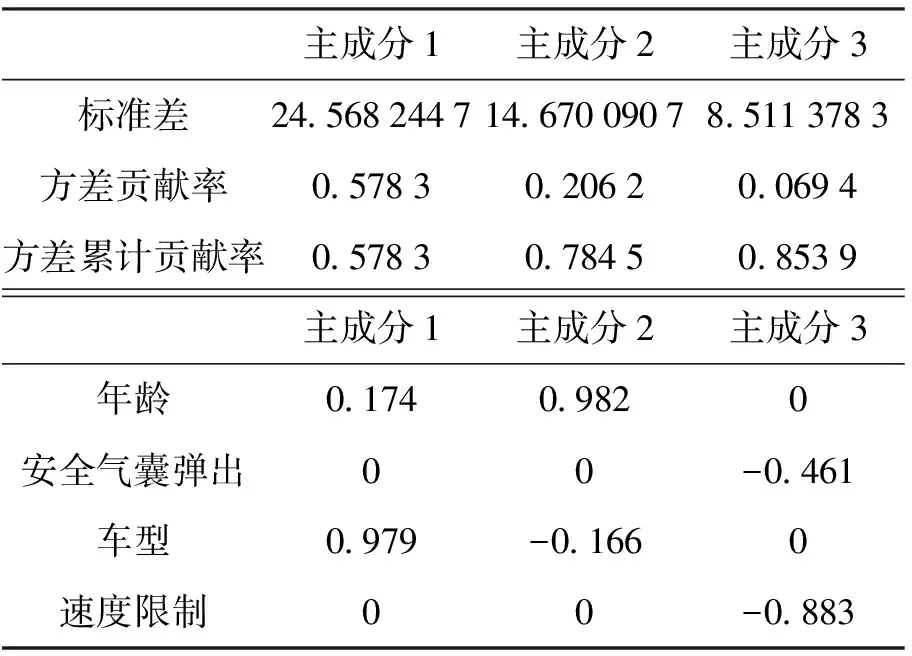
表1 主成分分析结果

3.3 OP模型检验与结果分析

利用Ordered Probit模型对PCA方法选择出的主要因素进行分析. 为了量化定性因素对因变量的影响，所有因素都采用哑变量方式，所得结果如表2.

表2 OP模型计算结果

OP模型分析的结果直接显示出各个属性相对于哑变量对事故伤害程度有多大影响，由表2可知：

1)年龄对伤害程度存在影响，但仅当置信水平水平为90%时可以接受这一假设，因此随着年龄的升高，交通参与者在事故中所受到的伤害并不会显著加重；

2)安全气囊的弹出可以显著降低人的受伤程度，为未弹出情况的0.747倍；

3)乘坐多用途车和中型、重型卡车的人，受伤害程度比乘坐小汽车的低，而摩托车驾驶者或乘坐者的受伤害程度明显偏高；

4)当限速超过60 km/h时，人的受伤程度相比低速状态显著升高，易出现重伤事故.

对模型进行似然比检验和拟合优度分析，结果见表3. 根据式(8)，L为Model1的LogLik值，为-2 033.6，L0为Model2的LogLik值，为-2 164.4，LR值即为Chisq，为261.5，它对应的P值小于2.2×10-16，因此，它是显著的，表明模型整体是显著的.

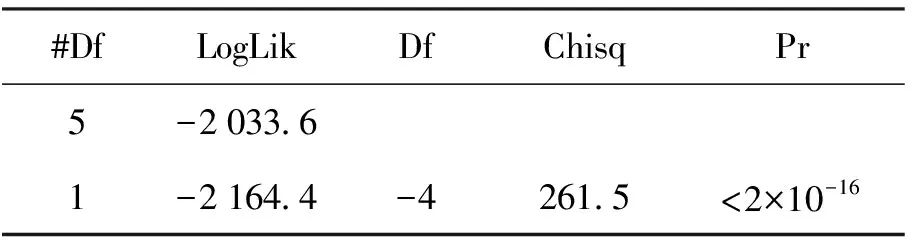
表3 似然比检验和拟合优度分析结果

4 结论

在以人为本思想的指导下，以降低高速公路交通事故对人员的伤害程度为目的，提出了一种交通事故伤害程度分析方法. 该方法利用主成分分析法从过多的影响因素中筛选主成分，并通过OP模型分析主成分对事故伤害程度的影响，最后从似然比检验和拟合优度检验2个方面验证了提出的方法正确性和有效性. 结果显示，安全气囊、车型和速度限制对事故伤害程度的影响显著. 所提出的方法具有一定的通用性，可以用于类似交通事故分析.

参考文献：

[1] Çelik A K, Oktay E. A comparison of ordered and unordered response models for analysing road traffic injury severities in the north-eastern Turkey[J]. Periodica Polytechnica Transportation Engineering, 2016(3): 12-14.

[2] Vesna Rovšek, Milan Batista, Branko Bogunovi. Identifying the key risk factors of traffic accident injury severity on Slovenian roads using a non-parametric classification tree[J]. Transport, 2014, 32(3): 272-281.

[3] 马壮林, 邵春福, 李霞. 基于Logistic模型的公路隧道交通事故伤害程度的影响因素[J]. 吉林大学学报: (工学版), 2010, 40(2): 423-426.

[4] Anowar S, Yasmin S, Eluru N, et al. Analyzing car ownership in Quebec City: a comparison of traditional and latent class ordered and unordered models[J]. Transportation, 2014, 41(5): 1013-1039.

[5] 李文权, 王炜. 交通事故的时间分布规律[J]. 中国安全科学学报, 2005, 15(4): 56-61.

[6] 马壮林, 邵春福, 董春娇, 等. 基于累积Logistic模型的交通事故伤害程度时空分析[J]. 中国安全科学学报, 2011, 21(9): 94-99.

[7] 李文权, 王炜. 交通事故的时间分布规律[J]. 中国安全科学学报, 2005, 15(4): 56-61.

[8] 马柱, 陈雨人, 张兰芳. 城市道路交通事故伤害程度影响因素分析[J]. 重庆交通大学学报: (自然科学版), 2014, 33(1): 111-114.

[9] Rao C R. The use and interpretation of principal component analysis in applied research[J]. Sankhyā: The Indian Journal of Statistics, Series A (1961—2002), 1964, 26(4): 329-358.

[10] Chernoff H, Lehmann E L. The use of maximum likelihood estimates in $chi^2$ tests for goodness of fit[J]. Annals of Mathematical Statistics, 1954, 25(3): 579-586.

[11] National Highway Traffic Safety Administration. National Automotive Sampling System (NASS)General Estimates System (GES) [EB/OL]. [2013. 3. 6]. https:∥www. nhtsa. gov/research-data/national-automotive-sampling-system-nass.