轮边直驱永磁盘式电机转矩脉动分析与抑制

(无锡智磁科技有限公司，江苏无锡 214100)

0 引言

永磁轮边直驱动力总成结构无论是高传动效率还是有效减少车体空间占用等方面，都明显优于集中驱动方式[1]。而相较于传统径向磁场永磁电机而言，轴向磁通永磁盘式电机拥有更高的功率密度和转矩密度，较好的散热能力[2]。对于轮边直驱电机而言，转矩输出的平稳性有着至关重要的地位，而转矩脉动一定程度上影响了电机输出转矩的平稳性，需要对电机转矩脉动进行优化设计。对于传统径向磁场电机而言，降低转矩转矩脉动的方法主要通过斜槽来抑制齿槽转矩脉动。文献[3]中的车用电机采用了定子斜槽技术降低电机的齿槽转矩。文献[4]分析了电动汽车用永磁无刷直流电机的齿槽转矩的影响因素，分析了斜槽角与齿槽转矩大小的关系并优化齿槽转矩。文献[5]介绍了通过永磁盘式电机定子加工斜槽在工艺上难度要复杂。文献[6]通过研究定子齿顶增加辅助槽的方式来减少齿槽转矩脉动，而对于通过斜极方式来降低永磁盘式电机转矩脉动的研究较少。

本文以一台功率6kW、额定转速933r/min轮边直驱永磁盘式电机作为研究对象，研究斜极形式对电机齿槽转矩与纹波转矩进行抑制，通过三维有限元仿真分析，以斜极角度为变量，分析不同斜极角度对电机转矩脉动的影响，从而达到减小转矩脉动的目的。电机相关设计参数见表1。

表1 电机主要参数

1 齿槽转矩与纹波转矩数学模型

1.1 齿槽转矩数学模型

齿槽转矩定义为电机不通电时磁场能量对定转子相对位置角的负导数，磁场能量见式(1)，齿槽转矩定义式见式(2)

(1)

(2)

式中，Br(θ,r)—永磁体剩磁；h(θ)—永磁体充磁方向长度；δ(θ,α)—气隙有效长度；θ—周向机械位置角；α—永磁体中轴线与定子齿中轴线错开的机械角度；r—径向位置变量。

磁极周向并联组合的轴向磁场永磁同步电机气隙磁密Br(θ,r)在内径r处分布示意图见图1所示。

对于图1气隙磁密波形经过傅里叶分解后可得

(3)

(4)

将式(3)、(4)代入式(1)、(2)，可得到轴向磁场永磁电机的齿槽转矩表达式见式(5)所示

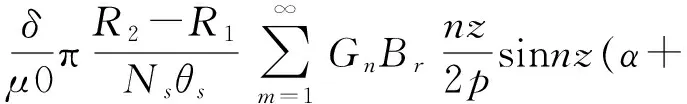
(5)

式中，Ns—定子斜槽数；θs—定子齿距弧度；R1—永磁体内径；R2—永磁体外径；m、n—谐波次数；z—定子单边槽数。

1.2 纹波转矩数学模型

影响轴向磁场永磁盘式电机的电磁转矩脉动因素除了齿槽转矩外，还与纹波转矩的转矩脉动有关，当忽略磁路饱和与电枢反应，不计齿槽转矩的影响，电机三相电流为理想正弦波时，电机存在6次及6的倍数次纹波转矩。电机的转矩可表达式见式(6)所示，平均转矩公式见式(7)所示，纹波转矩见式(8)所示

“再说了，不是战功累累的老兵，哪有资格配娶咱，你说是不？这也是组织上给予咱们的特殊荣誉咧。老话说，女大三抱金砖，我看是男大三，保平安。我家老刀可心疼我们母女仨，有啥吃的，都尽量留着丫头和我。冬天睡不暖，他总是抱着我的双脚，放在他胸口暖。”向阳花说着说着，眼泪一滚。“当年，也不肯嫁给他，死活不肯，和你一样瞎闹。走路一前一后，吃饭一里一外，睡觉一东一西，后来生了丫头，越过越觉得苦尽甘来，前两年还一家四口去照相馆照了全家福。现在觉得，嫁给老刀嫁对了。今生嫁给他不后悔。如有下辈子，下辈子还嫁给他。”

(6)

(7)

(8)

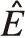
2 有限元模型建立与剖分误差分析

轴向磁场结构的永磁盘式电机磁路结构复杂，在有限元分析建模时通常建立三维模型，利用SolidWorks三维设计软件建立好模型后导入Maxwell 3D中，对电机各部件进行重新定义，图2为电机模型图，电机模型采用双定子单转子串联磁路结构，永磁体由转子盘固定。由于在使用Maxwell 3D中瞬态场对电机进行有限分析计算量比较大，为了缩短仿真时间，电机采用1/12模型进行研究，以提高仿真研究工作效率。

图2 电机模型图

利用Maxwell 3D对电机进行分析时，其计算误差除了与建模误差外，还与网格剖分精度有关，故在求解有限元模型时选取合适的网格剖分精度一方面有利于提高有限元计算精度，减少求解误差，另一方面缩短了仿真求解时间，提高研发效率。应用麦克斯韦应力法计算转矩时，对求解区域的剖分要求较为严格，求解区域包括定子齿部、永磁体、气隙区域。因为齿槽转矩对该求解区域网格变化比较敏感，在分析网格剖分时主要针对求解区域的单元剖分长度与齿槽转矩求解误差进行分析，表2是针对求解区域不同剖分单元长度下电机齿槽转矩求解值与前值的计算误差。

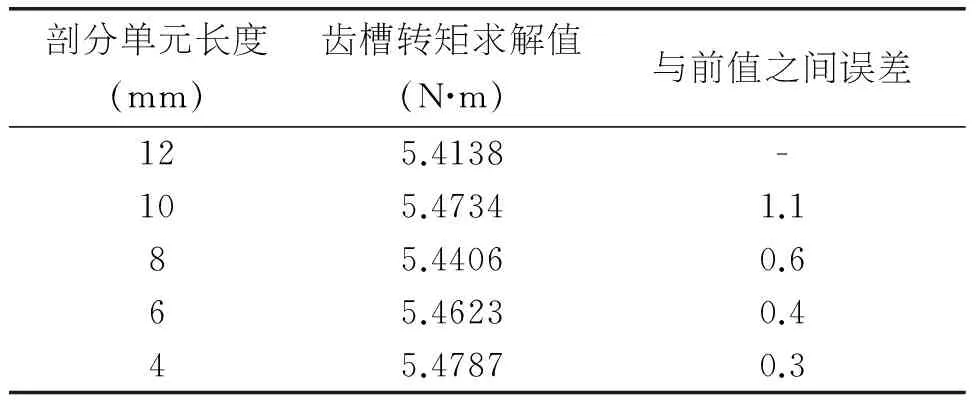
表2 不同剖分单元长度下的齿槽转矩求解误差

可以看出，随着剖分单元长度增加，剖分的精度将随之大为增加，当剖分达到一定密度后，齿槽转矩的求解值误差变化很小，再增加求解精度只会增加计算量和计算时长，对于减少误差并无显著作用，故当求解值误差小于0.5%，即视为网格剖分精度与求解结果影响无关。从而确定了求解区域网格剖分单元长度为6mm较为合适。图3为电机有限元网格剖分图，其中定子齿部、永磁体、气隙区域的剖分较密，剖分单元长度均设定为6mm。

图3 电机网格剖分图

3 电机转矩脉动优化分析

对于轮边直驱电机而言，转矩输出的平稳性有着至关重要的地位，而齿槽转矩的转矩脉动一定程度上影响了电机输出转矩的平稳性，需要对齿槽转矩进行优化设计。对于传统径向磁场电机而言，降低齿槽转矩的方法主要通过斜槽来抑制齿槽转矩脉动，而轴向磁场电机定子加工斜槽在工艺上难度要复杂一些，根据式(5)可知，轴向磁场永磁同步电机可以通过斜极方式来抑制齿槽转矩的转矩脉动，通过三维有限元仿真分析，以永磁体斜极角为变量，可得到斜极角对齿槽转矩的削减情况如图4所示，可以看出当永磁体斜极10度机械角时齿槽转矩由5.4N.m降低到0.9N.m，起到了显著的抑制效果。

图4 斜极角对齿槽转矩的削减情况

影响轴向磁场永磁盘式电机的电磁转矩脉动因素除了齿槽转矩外，还与纹波转矩的转矩脉动有关，当忽略磁路饱和与电枢反应，不计齿槽转矩的影响，电机三相电流为理想正弦波时，由式(6)可以看出相反电动势的基波大小决定了电机输出的平均转矩，由式(8)可以看出电机的相反电动势的6n+1和6n-1次谐波大小决定了电机的6n次纹波转矩。图5、图6为不斜极电机空载反电动势波形图和傅里叶分析图。

图5 不斜极电机空载反电动势波形图

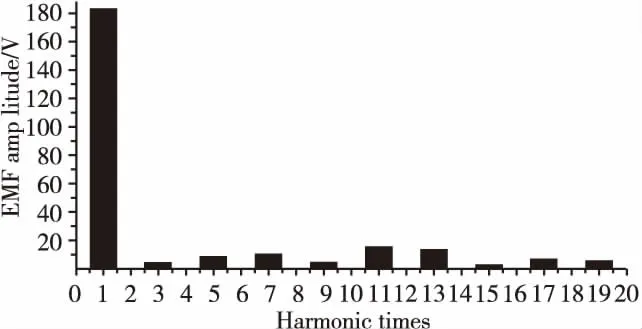
图6 不斜极电机空载反电动势傅里叶分析图

可以看出，电机的空载反电动势波形波峰较平，存在一定的谐波。对电机的空载反电动势波形进行傅里叶分解如图6所示，该电机11、13次谐波含量较高。

图7 不斜极转矩波形图

当电机定子结构尺寸以及绕组形式确定不变时，需要对转子结构进行改变才能削弱反电动势谐波，在轴向磁场永磁盘式电机中同样可采用转子斜极的方式，其作用是通过改变相反电动势谐波斜极因数和谐波磁密幅值来抑制纹波转矩。

将电机转子永磁体斜过10度机械角度后，傅里叶谐波分析图和电机的空载反电动势波形图见图8、图9所示。可以看出电机在斜极后的5、7、11、13次谐波均明显下降。

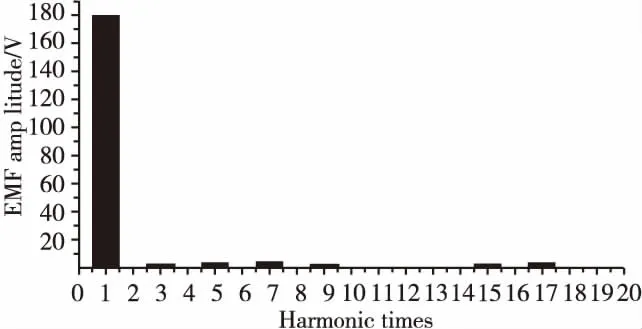
图8 斜极后电机空载反电动势傅里叶分析图

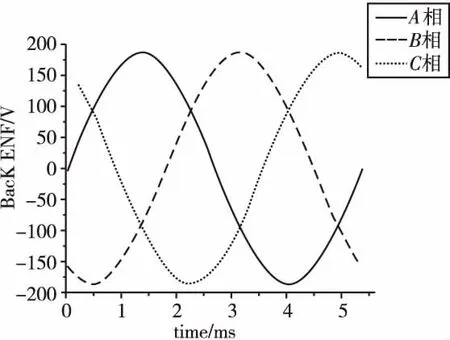
图9 斜极后电机空载反电动势波形图

图10为斜极后转矩波形图，可以看出电机经过永磁体斜极优化后，波纹转矩脉动的波动明显减小，纹波转矩脉动降低到3.6%，电磁转矩脉动下降到4.1%，转矩脉动优化显著。

图10 斜极后电机转矩波形图

4 结语

本文研究以一台6kW、933r/min额定转速轮边直驱永磁盘式电机为例，研究了不同斜极角对电机的转矩脉动影响，并得到了如下结论。

轴向磁场电机定子加工斜槽在工艺上难度要复杂一些，通过斜极方式来抑制齿槽转矩的转矩脉动，斜极角为10°时，齿槽转矩脉动最小。

相反电动势的基波大小决定了电机输出的平均转矩，电机的相反电动势的6n+1和6n-1次谐波大小决定了电机的6n次纹波转矩。将电机转子永磁体斜过10度机械角度后，电机的空载反电动势中的5、7、11、13次谐波均明显下降。通过使空载反电动势正弦化的方法是降低纹波转矩脉动的有效方法。

[1] 于新龙.电动汽车轮边驱动系统驱动方式与特点分析[J].汽车使用技术,2012，13(2):31-34.

[2] C.C.Chan.The state of the art of electric and hybrid vehicles. Proceedings of IEEE，2011，90(2)：247-275.

[3] 王晓远，严长伟．电动汽车用内置式永磁同步电动机转子结构优化[J]．微特电机，

2014，42(8)：26-33．

[4] 崔思鹏，王建辉，刘凯．永磁无刷直流电机齿槽力矩分析[J]．电器工业，2010，36(8)：34-39．

[5] 邹文，竺韵德，张钢．一种抑制永磁盘式电机齿槽转矩的新方法[J]．微特电机，2016，41(5)：12-18．

[6] Paulides J J H，Jewell G W，Howe D．An evaluation of alternative stator lamination materials for a high-speed，1.5 MW，permanent-magnet generator[J]．IEEE Transactions on Magnetics，2004，40(4)：2041-2043．

[7] 李延升，窦满峰，樊鑫．表贴式永磁电机气隙磁场及齿槽转矩解析计算[J]．微特电机，2012，40(12)：9-15．

[8] WANG D H，WANG X H，QIAO D W． Reducing cogging torque in surface-mounted permanent-magnet motors by nonuniformly distributed teeth method[J]．IEEE Transactions on Magnetics，2011，47(9)：2231-2239．