交流绕组理论的原概念和新术语及其关系第II部分：原概念与新术语之间的关系

2018-05-02

防爆电机 2018年2期

关键词：电机学对偶术语

(华南理工大学电力学院，广东广州 510640)

1 一些符号

1.1 p、2p、m、μ、Q、D

极对数，也就是阶数，用p表示。相数用m表示。方数用μ表示。槽数用Q表示。带数用D表示，有两层考虑：(1)District有“带、区”之意；(2)D是“带”字汉语拼音的声母。

1.2 Qp、Dp、q、d、a

每极每相槽数用q表示。每极每相带数用d表示，对六相30°相带、三相60°相带、两相90°相带而言，d都等于1。三相120°相带(d=0.5)仅有理论意义，无实用价值，因而下文不讨论。

每相并联支路数(相支数)用a表示。每阶槽数Qp，简称阶槽数。每阶带数Dp，简称阶带数。

2 一些关系式和关系表

基于前述，可得一些关系式如下。

一个电机的带数D=d×2pm=2pm。可见，带数就是“极数乘相数”，即“极相积”，亦即所有极下的总“相带”数。同时，D=2pm=p×(2m)。可见，带数也是“阶数乘方数”，即“阶方积”。这里为了新旧衔接，仍然借用“相带”这一旧术语。对于三相绕组，m=3，D=6p；对于单相电机，m=2，D=4p。即

带数D=极相积=阶方积

(1a)

D=2pm=p×(2m)

(1b)

每极每相槽数q=带槽数

(2a)

(2b)

一个电机的槽数Q=Dq=2pmq，即

槽数=带数×带槽数

(3a)

Q=Dq

(3b)

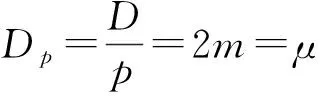
阶带数=倍相数=方数

(4a)

(4b)

带谐波(即传统的“相带谐波”)次数

v′=∓(kDp∓1)=∓(kμ∓1),k=0,1,2,3,…，∞；两个∓同正同负

(5)

阶槽数=阶带数×带槽数

(6a)

Qp=Dpq=μq

(6b)

槽谐波次数

v=∓(kQp∓1)=∓(kμq∓1),k=0,1,2,3,…，∞；两个∓同正同负

(7)

带谐波、槽谐波，两者的次数在形式上完全对偶，有一种美感。

方数=倍相数

(8a)

μ=2m

(8b)

综上，可得表1、表2。表1的特点是，右边量是左边量的2倍，或q倍。表2的特点是，左边量都含有“槽”字，右边量都含有“带”字。

3 一些概念的属性

相是外部观察量，方是内部观察量。

相、方，都不具叠加性。譬如，一个4极三相36槽60°带绕组，每一阶(对极)都有3相、6方。整个绕组也是3相6方。

极、带，都具有叠加性。譬如，一个4极三相36槽60°带绕组，每一阶(对极)含有2极、6带。整个绕组含有4极12带。

极、相、槽，阶、方、带，捉对对应：极对应阶，相对应方，槽对应带。具体对应关系是：两极构成一阶，两方构成一相，q槽构成一带。“极、相、槽”是已有的术语，“阶、方、带”是本文引入的术语。有了“阶、方、带”，绕组理论的术语系统才算完整。

4 对偶塔

据前述内容，可作“带槽对偶金字塔”(可简称“带槽对偶塔”，或者“对偶塔”)如图2所示。图2中箭头表示“除”，注意“除”和“除以”是不同的。图2包括了本文所提新术语之大部分。

图2中，阶数置顶，下面诸术语均围绕“阶”展开，可见“阶”之于绕组理论的极端重要性。另外，带槽数q反映了带、槽之间的联系，是沟通带、槽的“桥梁”，也很重要。

表1 一些符号列表

表2 一些关系式列表

图1 带槽对偶金字塔

图1直观地反映了槽、带之间的对偶关系。这种对偶关系，主要体现在槽谐波、带谐波两种谐波次数之间的对偶。为什么有这种对偶？深思细究不难发现，深刻原因在于：带乃大槽。同一带内各槽电流是一致的，就像同一槽内电流相同。这种一致性是空间分布意义上的，包括了大小和相位。因而可以认为，从电流空间分布的意义上来说，每一个带，就相当于一个槽。只不过同一带内含有多个槽，因而可以称之为“大槽”。而磁势波形仅取决于电流的空间分布。这一点，文献[2]第42页的磁势积分法、文献[16]的式(1-1)磁势安导积分关系，都有很清楚的解释。