探究一道高中数学联赛预赛题

虞 懿

浙江省金华市第六中学 (321000)

我们知道，数学学习离不开解题，解题教学更是数学教学的重心，从而例题的选择与讲解就显得尤为重要．竞赛(高考)试题是命题专家集体智慧的结晶，其背后蕴藏的知识、思想与内在本质，体现出学科课程教学的重心和导向.因此，研究竞赛(高考)试题具有非常现实的指导意义和教学价值．本文通过对一道高中数学联赛预赛题的深入研究，旨在挖掘试题背后的内涵，彰显其数学魅力．

1.考题呈现

(1)求满足上述条件的点P(x,y)的轨迹方程；

(2)设A(-1,0),F(2,0)，问是否存在常数λ(λ>0)，使得∠PFA=λ∠PAF恒成立？证明你的结论．

2.解析品读

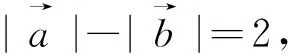
(2)在第一象限内作PF⊥x轴，则P(2,3)，此时∠PFA=90°,∠PAF=45°,λ=2．

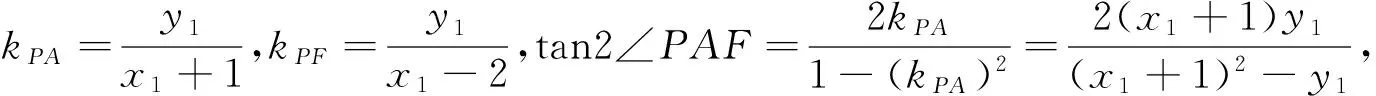
品读：本题第(1)问求动点的轨迹方程，这是解析几何的重要内容，也是高考命题的热点和重点．主要考查学生的数形结合、等价转化、逻辑推理、合理运算、分类讨论及创新思维能力．第(2)问是一道返璞归真的探索性问题，其立意之新、内涵之广、选材之妙不得不令人叹服．以新颖的视角、创新的手法进行精心的构思，彰显新课程的理念，所以是一道创新而不落俗套的好试题，有利于甄别学生的思维层次，具有较好的区分度．

3.引申拓展

“探幽重门深锁无寻处，疑有碧桃千树花．”对于一个数学问题，需要多角度的剖析、探究．对于一个数学问题的探究思考，最基本的切入点就是对条件与结论进行变式思考，可以考虑在这些情况下结论是否成立．

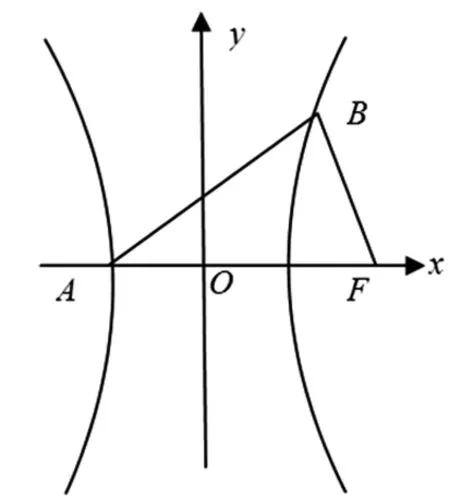
图1

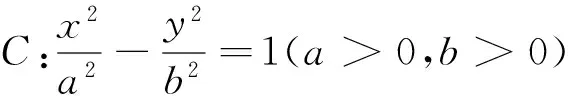
证明：如图1所示，设A(-a,0),F(c,0),B(x0,y0)(x0≥a).

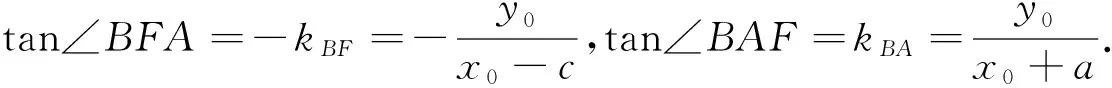
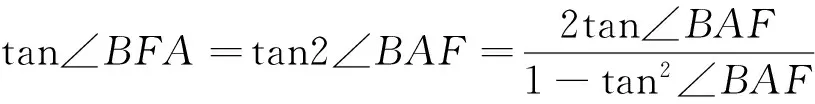
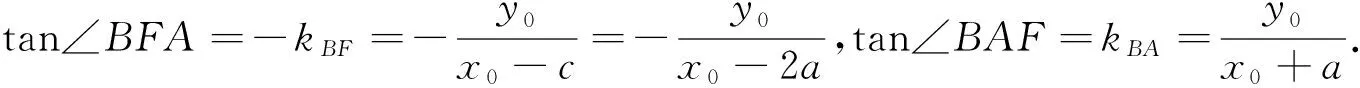
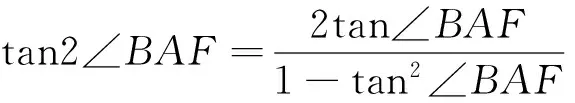
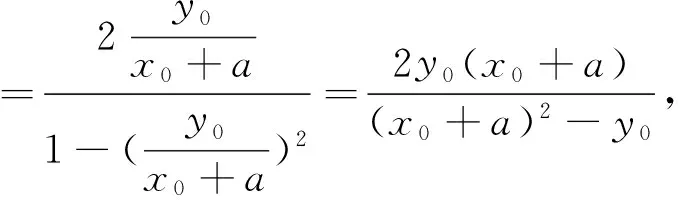
当x0=c时，易得∠BFA=2∠BAF,综上可得∠BFA=2∠BAF.

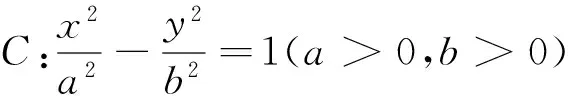
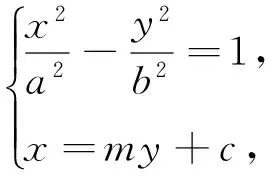
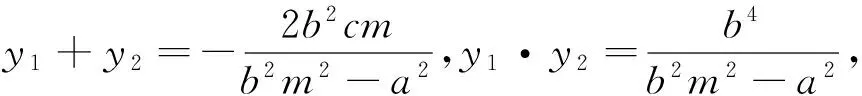
(充分性)由必要性的证明过程可证．

4.题源链接

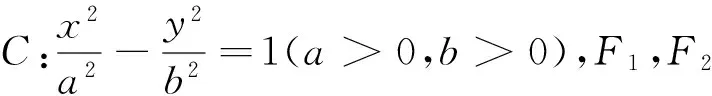
(Ⅰ)求C的离心率e；

(Ⅱ)设A为C的左顶点，Q为第一象限内C上的任意一点，问是否存在常数λ(λ>0),使得∠QF2A=λ∠QAF2恒成立若存在，求出λ的值；若不存在，请说明理由．

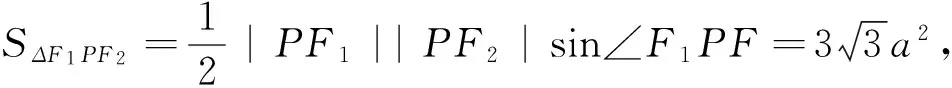
cos∠F1PF2,即4c2=16a2,从而e=2.

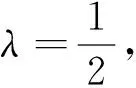
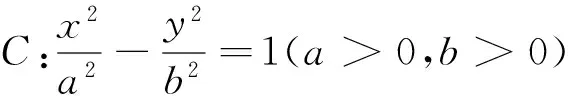
(Ⅰ)求双曲线方程；

(Ⅱ)设Q为双曲线C右支上动点，F为双曲线C的右焦点，在x轴负半轴上是否存在定点M使得∠QFM=2∠QMF?若存在，求出点M的坐标；若不存在，请说明理由．

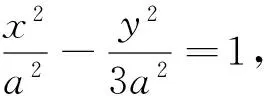
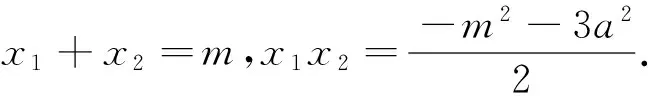
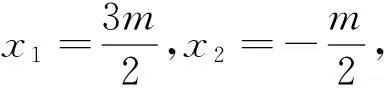
(Ⅱ)由双曲线离心率为2,得b2=3a2,再由上述结论1可知存在定点M(-1,0)使得∠QFM=2∠QMF.

5.探究感悟

美国著名数学家G·波利亚曾说过：“解题是一种实践性的技术，就像游泳滑雪或者弹钢琴一样，只能通过模仿和实践学到它……你想游泳就必须下水，你想成为解题能手就必须去解题．”然而过多机械化地、重复地训练，会导致忽略问题的本质，忽视问题的内在联系．在数学学习过程中，积极寻找问题的本质，把握数学知识的多样联系，掌握数学思维方法，体验数学的理性精神，通过追根溯源，触类旁通，去探究问题的本质，以达到提高解题效率，提升解题能力的目地．