巧用仿射变换解决高考中解析几何问题

王子怡 赵临龙(指导教师)

陕西安康学院数学与统计学院 (725000)

与椭圆相关的问题一直是高考中的重点、热点问题.由仿射变换可以将椭圆转化为圆，结合圆的性质求解问题大大降低运算量，节省了运算时间，也在一定程度上拓宽了研究问题的视野.

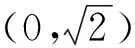
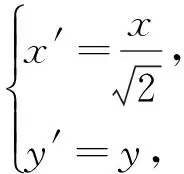
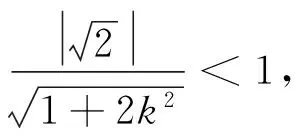
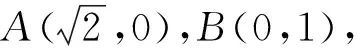
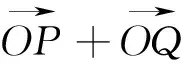
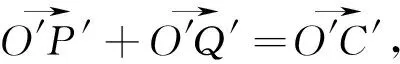
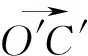
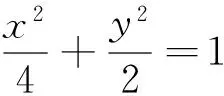
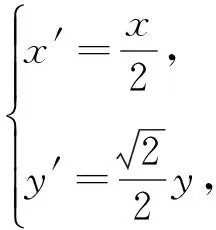
设点A,B,C,P变换后的对应点为A′,B′,C′,P′,不妨设点P′坐标为(n,m),则C′坐标为(n,0).

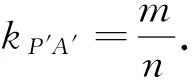
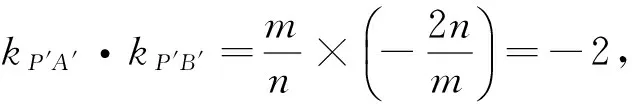
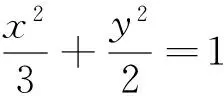
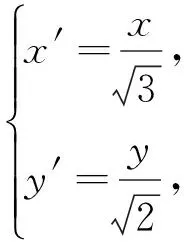
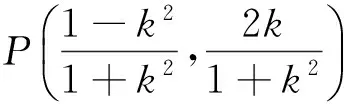
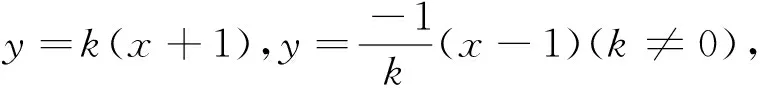
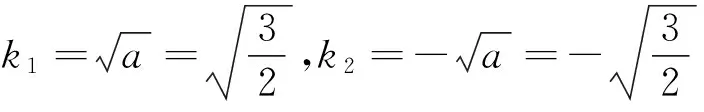
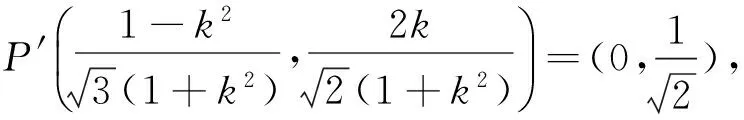
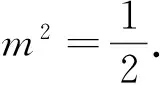
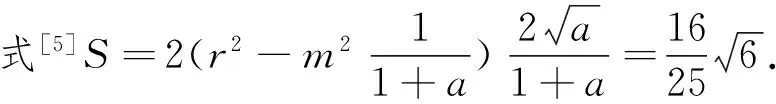
例4[5](2015年全国卷Ⅱ理20)已知椭圆C:9x2+y2=m2(m>0)，直线l不过原点O,且不平行于坐标轴，l与C有两个交点A,B,线段AB的中点为M.

(1)证明：直线OM的斜率与直线l的斜率的乘积为定值；

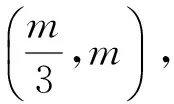
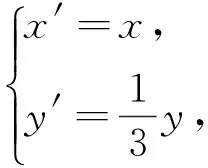
因为变换后O′M′⊥A′B′(垂径定理),∴kOM′·kA′B′=-1.∴kOM·kAB=-9.

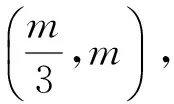
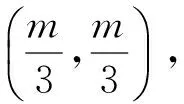
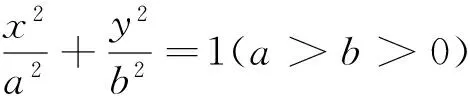
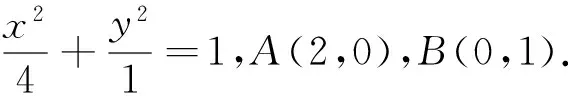
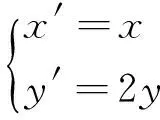
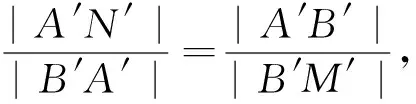
|A′B′|2=8,∴|AN|·2|BM|=8.

∴|AN|·|BM|=4.

与参考答案相比较，上述问题利用仿射变换的解法大大降低了利用解析几何解题的计算量，解题思维也更加流畅，更能接近问题的本质.

[1]贾慧美，基于仿射变换下对椭圆的探讨[J].数学教学通讯，2017.12.

[2]周涛，2011年江苏卷18题的解题研究[J].数学教学研究，2012.2.

[3]周振荣，赵临龙，高等几何[M].武汉:华中师范大学出版社，2013.

[4]彭耿铃，巧用仿射变换妙解一类解析几何问题[J].数学通讯，2016.z4.

[5]赵临龙，封闭二次曲线内接四边形面积最值新探[J].河南科学，2011.11.

[6]唐绍友，2016年北京市高考数学试题特点及教学建议[J].中国数学教育，2017.2.