高中函数零点问题的求法探析
2018-05-02江智如
江智如
福建省南平市高级中学 (353000)
1.问题提出
函数的零点问题是近些年高考的热点,因其涵盖知识广,综合性强,不仅可以考查高中学生的运算能力和化归思想素养,也能很好地体现试卷的区分度,因此零点问题成为各类综合试卷与练习的常客.但它也是高中学生比较畏惧的难点之一,许多考生对这类问题束手无策,往往只能放弃,甚为可惜.基于此,本文从提高高中学生的学习效率和做题质量,培养高中学生逻辑推理和数学运算素养的角度出发,探析解决零点问题的有效方法.
2.概念界定
对于函数y=f(x),把使f(x)=0的实数x称为函数y=f(x)的零点.即函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图像与x轴交点的横坐标,二者是等价的.在日常的教学过程中可“结合二次函数的图像,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程根的联系”.
3.方法探析
在课标课程中,常见的函数零点问题有两类:(Ⅰ)函数零点(方程根)的求解与判定问题;(Ⅱ)以函数零点(方程根)为载体的参数求解问题.
3.1 函数的零点(方程的根)的求解与判定问题
3.1.1 判断函数的零点(方程的根)的个数
若函数表达式能够因式分解,一般采用直接求零点的方法,即:令f(x)=0,通过因式进行求解,有几个解就是有几个零点.这类问题主要考查高中学生的运算能力,也就是多项式分解的能力,大部分的高中学生都能解决.
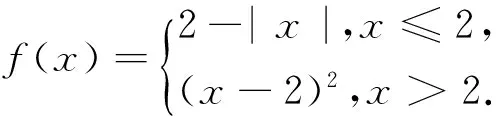
分析:本题考查高中学生对函数概念及分段函数的理解与掌握.因为f(x)是一次和二次的解析式,问题可转化为直接求方程f(2-x)=3的解.先求得f(2-x)的解析式,再进行求解,最终得到y=g(x)的零点个数为1.
点评:对于由初等函数简单组合的函数或方程,一般通过直接求解的方式进行解决,这类问题主要考查高中学生的因式分解与运算能力,得分率较高,学生的完成情况较好.
3.1.2 函数的零点所在区间的判定
对于无法直接求解的函数,可从函数零点存在性定理(介值定理)着手.求解步骤为:(Ⅰ)函数f(x)在区间[a,b]上是连续不断的曲线;(Ⅱ)f(a)·f(b)<0;(Ⅲ)结合函数的图像与性质(如单调性、奇偶性、周期性)确定函数的零点个数.
例2 (2013重庆理6)若a A.(a,b)和(b,c)B.(-∞,a)和(a,b) C.(b,c)和(c,+∞)D.(-∞,a)和(c,+∞) 分析:本题是零点问题的概念题,考查定理的理解和方程的运算能力.根据题意分别求解f(x)在a,b,c三处的函数值,判断正负关系,得到结果为A. 如同课程中所讲,沟通问题会激发强烈的情绪。在尝试解决沟通问题时,首先要明确表达自己的情绪,坦承自己感受有助于缓和个人情绪。在控制情绪的基础上,做到中立的评估事实,然后进行有效的沟通而不是对峙。使用非对抗性的语言清楚的表达自己的意思是有效的手段。而我在初次和项目长沟通受到质疑时,并没有正确的分析问题,尝试有效的沟通。后来在与项目其他成员沟通时没有控制住自己的个人情绪,陷入了对峙的状态,采用了对抗性的语言,并把对方置于自己的对立面,最后冲突也无法得到有效的解决。 点评:对于判定零点区间的问题,一般利用连续函数的零点存在性定理判断函数值的正负情况,结合函数的单调性进行求解,考查高中学生运算求解和推理论证能力. 3.1.3 函数的零点、方程的根与函数图像的交点三者之间的互相转化 利用函数图像的交点来求解零点个数的问题.首先把方程转化为初等函数等式,然后分别画出等式两边初等函数的图像.判断其是否相交,若相交,交点的个数有几个,则相应的交点横坐标就有几个不同的值,函数就有几个不同的零点,从而得到原方程的实数根的个数;若不相交,则函数没有零点,亦即方程无实数根. 例3 (2017江苏14)设f(x)是定义在上且周期为1的函数,在区间[0,1)上,其中集合则方程f(x)-lgx=0的解的个数是 . 分析:本题考查数论的相关知识,难度较大,考查高中学生的逻辑推理和运算能力.因为D是有理数集的子集,且D⊆[0,1),同时在区间[0,1)上,f(x)∈[0,1),故lgx=f(x)∈[0,1),因此可以考虑1≤x<10的情况.利用f(x)的周期性与y=lgx的单调性,结合二者的图像得到方程解的个数为8. 点评:本题的设计,让考生体会到有理数集与无理数集之间紧密关系的思想与方法,这不仅能提高高中学生的逻辑推理能力,也能有效地培养高中学生的数学素养. 以函数零点(方程根)为载体的参数问题,考查高中学生对问题的理解及综合地应用知识分析、解决问题所需要的抽象概括能力和推理论证能力,考查创新意识,常用3种方法求解. 3.2.1 直接法:根据已知条件构建关于参数的不等式(组),通过求解不等式(组)确定参数 点评:本题考查了分类讨论和化归的数学思想.通过函数的单调性和y截距的定义,利用两个函数的图像关系,得到不等式组进行求解,使问题变得直观、简单,体现了数形结合思想的有效性. 3.2.2 分离参数法:根据解析式将参数分离,转化成函数值域问题加以解决 点评:分离参数法是解决零点问题的有效方法,考查高中学生的化归思想和数据运算能力,高中学生理解和掌握情况较好,但困难在于方程的化简和运算上,在日常的练习中可加以训练. 3.2.3 数形结合法:将解析式变形,画出相应函数的图像,利用数形结合的方法加以解决 分析:本题可从图像入手,利用数形结合的方法,转化为函数y=f(x)与y=b的交点个数问题.因为y=x3与y=x2的交点为(0,0)和(1,1).由幂函数的图像可求得,当a<0或a>1时,满足条件,故a的取值范围是(-,0)∪(1,+). 点评:数形结合是零点问题中常用的思想方法,运用数形结合思想,可以使抽象的零点问题直观化、形象化,能够变抽象思维为形象思维,有助于把握零点问题的本质,发现解题思路,能避免复杂的计算与推理,简化解题过程. 函数零点是综合性的问题,其解决方法不是单一绝对的,常需要以上多种思想与方法的结合才能解决,它能够培养高中学生函数与方程化归的思想、数形结合的应用意识.因此,在具体的教学实践过程中,可从“结合初等函数的图像,了解函数的零点与方程根的联系,判断方程根的存在性及根的个数”的角度进行思考与探究.3.2 以函数零点(方程根)为载体的参数求解问题
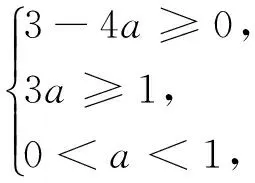

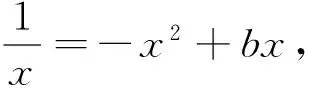
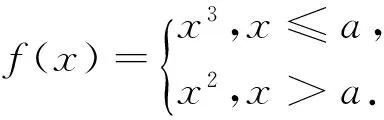
4.方法总结
