四步搞定含参数分段函数的最值问题

王启铸

山东省诸城繁华中学 (262200)

近年来，在数学竞赛及高考题中出现了一类题型，就是以含参数分段函数为背景的函数最值问题，考生在解答此类题时感到比较棘手，笔者经过研究得出了程序化的解题过程，只要按四步操作即可.希望对大家有所启迪.

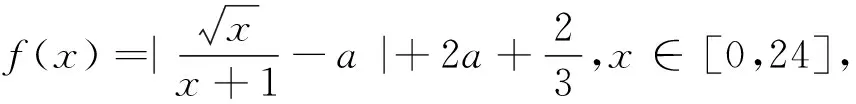
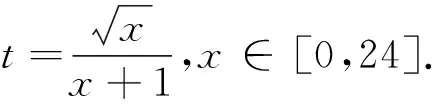
(Ⅱ)求M(a)；

(Ⅲ)省政府规定，每天的综合放射性污染指数不得超过2，试问目前该市市中心的综合放射性污染指数是否超标．

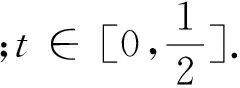
四步求解：

(1)先求分段函数：

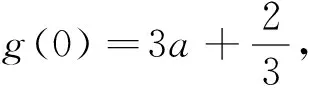
(3)比较两段上两个最值的大小，从而确定分段函数g(t)的最大值：

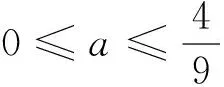
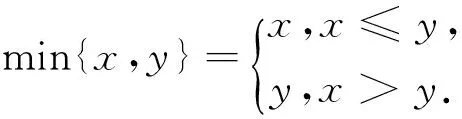
(Ⅰ)求使得等式F(x)=x2-2ax+4a-2成立的x的取值范围;

(Ⅱ)(ⅰ)求F(x)的最小值m(a);

(ⅱ)求F(x)在[0,6]上的最大值M(a).

解：(Ⅰ)略；当2≤x≤2a时，F(x)=x2-2ax+4a-2；

(Ⅱ)(ⅰ)是一个含参的分段函数最小值问题，可由四步式：

(1)先求分段函数：由(Ⅰ)知

(2)再求每一段上的最小值：当2≤x≤2a时，F(x)的最小值为-a2+4a-2；当x>2a或x<2时，F(x)的最小值为0;

(3)比较两段上两个最小值的大小，从而确定分段函数F(x)的最小值：

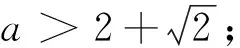
(4)下结论：

(ⅱ)依然是一个一个含参的分段函数最大值问题，可由四步式：

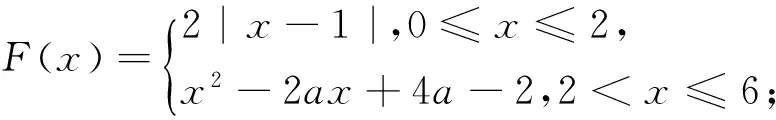
(2)再求每一段上的最大值：当0≤x≤2时，F(x)的最大值为2；当2

(3)比较两段上两个最值的大小：虽然在20，得3≤a<4；令32-8a<0，得a≥4；