一道预赛题的多种解法

金国林

浙江市宁波市镇海中学 (315200)

一题多解是指从不同的角度，运用不同的思维方式来解决同一道题.它有利于培养学生的发散性思维，深化思维活动，激发学习兴趣，优化学生的数学素质，从而提高教学质量.因此在高中数学拔尖创新人才培养的教学过程中，适时的引入一题多解是必要的，同时在实际教学中也是无法回避的.本文就笔者最近碰到的一道2016年江西预赛题，根据学生不同思维方式整理得到四种解法，以餐读者.

试题设x、y、z为正数，满足xy+yz+zx=1．证明：xyz(x+y)(y+z)(z+x)≥(1-x2)(1-y2)(1-z2)．

法1：原不等式等价于xyz(x+y+z)≥1-(x2+y2+z2)+(x2y2+y2z2+z2x2)，即xyz(x+y+z)≥(xy+yz+zx)2-(x2+y2+z2)(xy+yz+zx)+(x2y2+y2z2+z2x2),即证x3(y+z)+y3(x+z)+z3(x+y)≥2(x2y2+y2z2+z2x2),即证xy(x-y)2+yz(y-z)2+xz(x-z)2≥0，显然成立．

评析：通过“1”的巧用进行整体齐次化处理，再化简整理，这是处理此类问题的基本方法，是一种通性通法．

法2：由条件知x,y,z至多一个大于1，若恰有一个大于1，则原式显然成立；

若x,y,z∈(0,1]，则原不等式等价于2(x2+y2+z2)-2(xy+yz+zx)≥2(x2y2+y2z2+z2x2)-2xyz(x+y+z),即证(x-y)2+(y-z)2+(z-x)2≥x2(y-z)2+y2(x-z)2+z2(x-y)2,即证(1-x2)(y-z)2+(1-y2)(x-z)2+(1-z2)(x-y)2≥0，成立．

评析：直接展开进行配方和因式分解，再根据情况进行分类讨论，简单有效．

法3：设m=x+y+z,n=xyz，∵x+y+z>(x+y)(y+z)(z+x),∴xyz(x+y+z)≥xyz(x+y)(y+z)(z+x)≥(1-x2)(1-y2)(1-z2),故原不等式等价于xyz(x+y+z)≥(1-x)(1-y)(1-z)(1+x)(1+y)(1+z),即证mn≥(2-m-n)(2+m+n),即证m2+3mn+n2≥4.

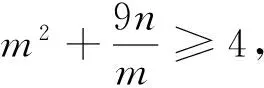
评析：由于本题是对称多元不等式，利用基本对称式进行换元转化，再联想到处理齐次对称不等式的利器——舒尔(schur)不等式，题目迎刃而解．

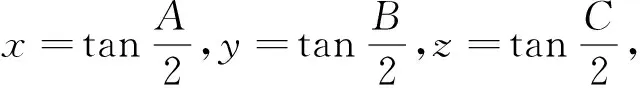
根据对称性，不妨设π>A≥B≥C>0，则不等式等价于

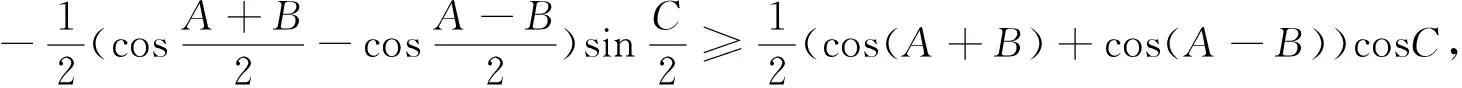
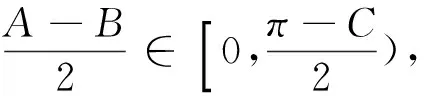
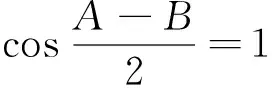
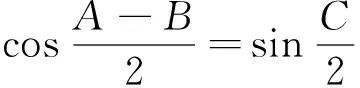
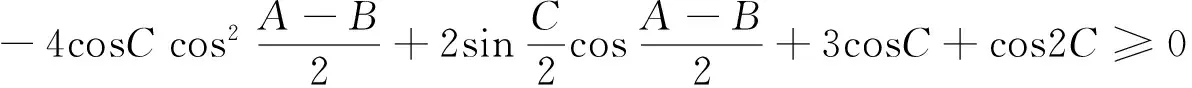
评析：由题目条件xy+yz+zx=1，学生容易想到利用三角换元进行尝试，但对后续三角不等式的处理有一定难度，需要较强的三角恒等变形能力．

[1]2016年全国高中数学联赛江西赛区预赛[J]．中等数学，2017(5).