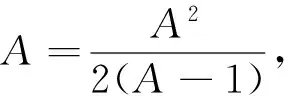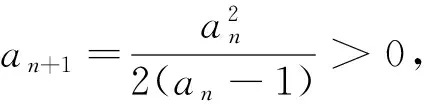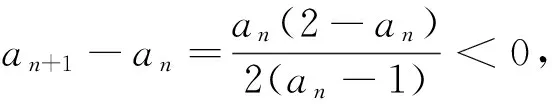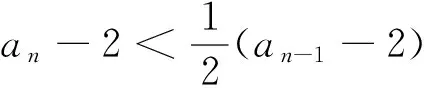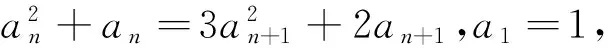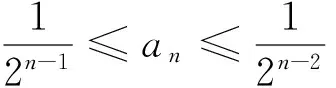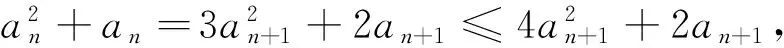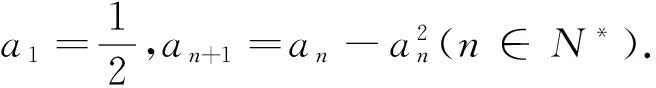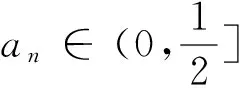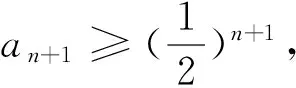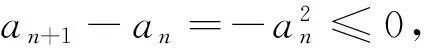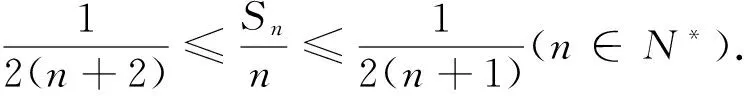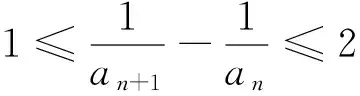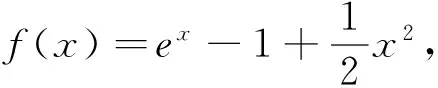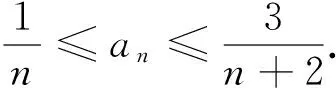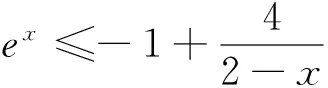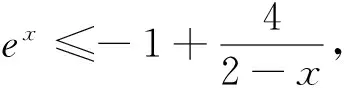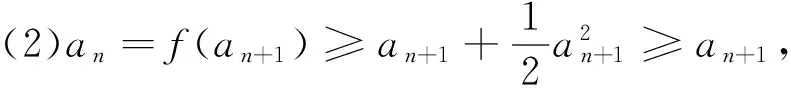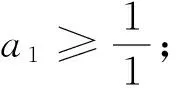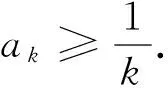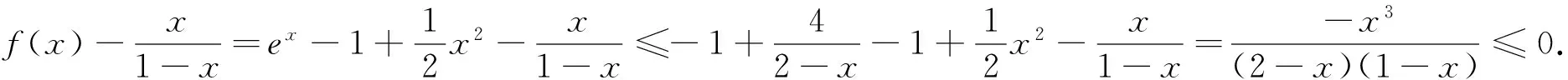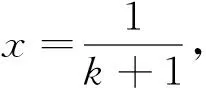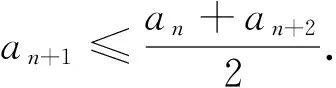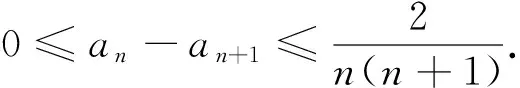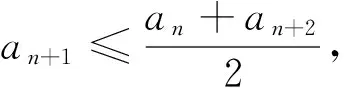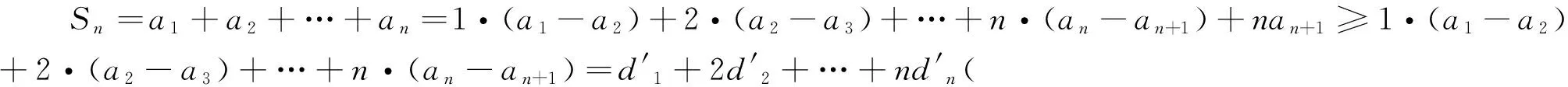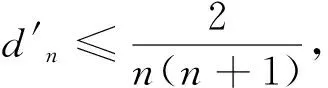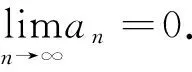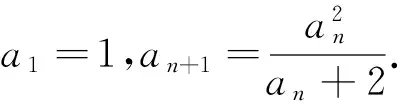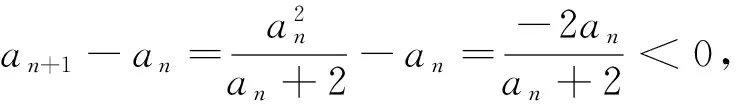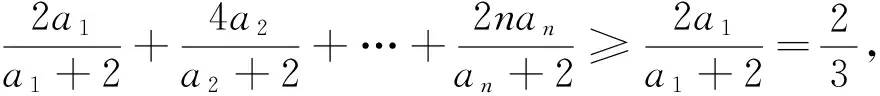例析数列不等式放缩技巧

王希年

浙江省杭州高级中学 (310003)

放缩法怎样讲，才会有效果呢？降低难度、放慢节奏是肯定的，讲思路、讲原理少不了，多次重复很重要，还必须对放缩技巧进行全面的归纳总结.

根据题目特点，本文在此着重介绍与数列极限引出的放缩技巧，供大家教学时参考.

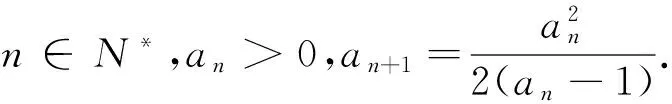
(1)求证：an>2且an+1

(2)证明：a1+a2+…+an<2(n+a-2).

分析：如果对已知等式两边取极限，极限是多少呢？

点评:在该数列的通项公式不能求出的情况下，通过放缩，得到不等关系的递推式，继而得到大比(小比)数列，运用递推(累乘)证得该数列不等式.

分析：构造函数求导做第一问，第二问左、右端为分式，极限为0，尝试累加.

点评:第一问是第二问的桥梁，如果用大比数列缩小，会缩得过小.

(1)若a1=1,a505=2017，求a6的最大值；

若at=0，则1≥Sn>(n-1)·min{at-1,at+1}，当n→∞时，上式不可能恒成立，

若at<0，1≥Sn>nat恒成立，但这与“各项均为非负数”矛盾.

所以对任意n∈N*，dn=an-an+1≥0.

其中的a1+a2+…+an=1·(a1-a2)+2·(a2-a3)+…+n·(an-an+1)+nan+1为阿贝尔变换.

为了让学生更好地掌握数列不等式放缩技巧，通过以上探究，本人所任班级学生大都能掌握数列不等式放缩技巧，有时能提供多种放缩方法，这是一件值得欣慰的事情.不等式放缩属于函数逼近论范畴，高难技巧令人望而却步，但每出现一个漂亮的不等式，都是一个视觉震撼，这是数学优生喜欢数学的一个理由.