模糊关系方程极小解的一种判别方法
2018-04-28林海涛杨晓鹏
林海涛, 杨晓鹏
(韩山师范学院 数学与统计学院, 广东 潮州 521041)
Sanchez[1-2]第一次提出了含max-min合成算子的模糊关系方程并进行开创性的探究之后,模糊关系方程开始被应用于多个领域[3-6],诸如模糊逻辑推理、人工智能、模糊决策和图像处理.后来,学者又致力于含max-product合成算子的模糊关系方程[7-9]的研究,并在诸多领域得到广泛的应用[10-13].max-min和max-product是最基本的2个模糊关系运算.经典的Max-T(T表示连续三角模,包含min和product等)模糊关系方程或不等式的解集由其唯一的最大解和有限个极小解所完全确定[14-15].一般情况下,最大解是容易得到的,因此获得解集的关键就是求出全部的极小解.对于解集或极小解集的求解方法,可以参阅文献[17-20].然而,求出模糊关系方程的极小解是一个NP困难问题,一般都不容易.对于一些具体的问题,并不需要求出全部的极小解,而只需判断一个解是否模糊关系方程的极小解.正是基于这样的考虑,本文将研究含max-min算子和max-product算子的模糊关系方程的极小解判别方法,并给出具体的判别步骤.
含max-min合成算子的模糊关系方程,其型如:
(1)
在系统(1)中,aij,bi,xj∈[0,1],i∈I={1,2,…,m},j∈J={1,2,…,n},而且a∧b表示求a、b的最小值,a∨b表示求a、b的最大值.
系统(1)可以记为
(ai1∧x1)∨(ai2∧x2)∨…∨(ain∧xn)=bi,i∈I,
或简单记为
A·xT=bT,
其中,A=(aij)m×n,b=(bi)1×m,x=(xj)1×n.
含max-product合成算子的模糊关系方程,其型如:
(2)
其中,A=(aij)m×n,b=(bi)1×m,x=(xj)1×n,aijxj表示普通的乘积.
系统(2)可以记为
ai1x1∨ai2x2∨…∨ainxn=bi,i∈I,
或简单记为
A·xT=bT.
为方便表达,在证明过程中仅以系统(1)的运算为例,即采用max-min合成算子,推导得到系统(1)的相关结论.对于系统(2),由于利用相似的方法也可以得到相关结论,因此文中只给出相应的结果,而不再详细证明.
如果系统(1)存在可行解,即存在x∈[0,1]n,使得A·xT=bT成立,那么称系统(1)为相容的;否则,称系统(1)为不相容的.系统(1)的所有可行解构成的集合记为X(A,b).
1 预备知识

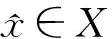




(3)

定理2[14]若系统(1)是相容的,记X=[0,1]n,则(1)的所有解集为:


2 模糊关系方程极小解的判别定理


记
Ji={j|Ai·(x*j)T=bi,j∈J},

即J0表示x*的分量为0的指标集.显然Ji、J0都是J的子集.
定理3若x*为系统(1)解,则对任意i∈I,Ji≠Ø.


即Ai·(x*j0)T=bi.因而j0∈Ji.从而Ji≠Ø.证毕.
可知,对于任意i∈I,Ji≠Ø.因而Ji至少含有一个元素,至多含有n个元素.记Ω={Ji|Ji为单元素集,i∈I}.
定理4(必要条件1) 若x*为系统(1)的解,则x*为极小解的必要条件是
(4)
其中,Ω为如上定义,即所有为单元素集的Ji的集合.





事实上对于任意i∈I,



注1定理4给出的是极小解的必要条件,但不是充分条件.例如,对于
(0.4∧x1)∨(0.5∧x2)=0.4,

为了寻求极小解的充分条件,引进下面记号.


事实上,对于固定的j∈J,Ji={j}意味着存在唯一的x*j使得第i个等式成立.当然,x*j可能使得多个等式成立,而且这些等式的指标构成的集合就是Ωj.可见Ωj⊆I.


事实上,xα与x*仅在第j0分量不同,其它相同.因而,只需要考虑指标属于Ωj0的那些方程.由Ωj0定义,对任意i∈Ωj0,有


另一方面,由于xα 这说明找到比x*还小的解xα,此与x*为极小解矛盾.证毕. 例1设max-min模糊关系方程组为 验证下面的向量是否模糊关系方程组(5)的极小解: 解(i) 对于x(1),易验证它不是(5)式的解,因而不是极小解. 定理6(充分条件) 设x*为系统(1)的解,则x*为极小解的充分条件是: 对任意ε=(ε1,ε2,…,εn)>0,令 由于Ji0={j0}为单元素集,因而对任意j≠j0,总成立 即bi0>Ai0·(x′)T,从而x′∉X(A,b).由命题1,x*为极小解.证毕. 综合定理4~6可以得到: 定理7(充要条件) 设x*为系统(1)的解,则x*为极小解的充要条件是: 定理8若x*为系统(2)的解,则对任意i∈I,Ji≠Ø. 证明略(类似定理3). 定理9设x*为系统(1)的解,则x*为极小解的充要条件是 (6) 证明略(类似定理4及6). 注3定理7用来检验max-min模糊关系方程的解是否是极小解,定理9则是max-product模糊关系方程的解是否是极小解的充要条件.虽然均是以指标的形式表达,但记号(4)与(6)所表达的运算基础不同.另外,对于前者,其充分条件比较“严格”,原因是需要考虑到min运算的性质.而对于后者,只需要考虑指标集是否满足(6)的关系. 基于定理4~7(定理9),给出max-min(max-product)模糊关系方程的极小解的判别算法. Step1检验x*是否为系统(1)(系统(2))的可行解.若不是,则x*非极小解;若是,转向Step2. Step2写出x*1,x*2,…,x*n. Step3计算出J0、Ji及Ω,i=1,2,…,m. 例2设max-min模糊关系方程组与例1相同,验证下面的向量是否模糊关系方程组(5)的极小解: (iv)x(4)=(0,0.3,0.7,0.4); (v)x(5)=(0.3,0,0.7,0.4). 解(iv)对于x(4),易验证它是(5)式的解,并且J0={1},J1={3},J2={3},J3={3},J4={2},J5={4},Ω={J1,J2,J3,J4},故 例3设max-product模糊关系方程组为 (7) 验证下面向量是否模糊关系方程组(7)的极小解: (i)x(1)=(0.8,0.75,0,1); (ii)x(2)=(0.8,0.75,0,0); (iii)x(3)=(0.8,0,0,1); 解(i) 对于x(1),易验证它是(7)式的解,并由x*1=(0.8,0,0,0),x*2=(0,0.75,0,0),x*3=(0,0,0,0),x*4=(0,0,0,1),得J0={3},J1={1},J2={2,4},J3={2,4},Ω={J1}.由于 因而x(1)不是极小解. (ii) 对于x(2),易验证它是(7)式的解,并且J0={3,4},J1={1},J2={2},J3={2},Ω={J1,J2,J3}. (iii) 对于x(3),易验证它是(7)式的解,并且J0={2,3},J1={1},J2={4},J3={4},Ω={J1,J2,J3}. (iv) 对于x(4),易验证它是(7)式的解,并且J0={1,2},J1={3},J2={4},J3={4},Ω={J1,J2,J3}. (iv) 对于x(5),易验证它是(7)式的解,并且J0={1,4},J1={3},J2={2},J3={3},Ω={J1,J2,J3}. 由于(ii)、(iii)、(iv)、(v)满足 根据定理9,x(2)、x(3)、x(4)和x(5)是系统(7)极小解. 致谢韩山师范学院博士启动项目(QD20171001)对本文给予了资助,谨致谢意. [1] SANCHEZ E. Equations de Relations Floues[M]. Marseille:These Biologie Humaine,1972. [2] SANCHEZ E. Resolution of composite fuzzy relation equations[J]. Information and Control,1976,30(1):38-48. [3] SANCHEZ E. Solutions in composite fuzzy relationequations:application to medical diagnosis in Brouwerian logic[C]. Gupta M M, Saridis G N, Gaines B R. Fuzzy Automata and Decision Processes. Amsterdam:North-Holland,1977. [4] NOBUHARA H, BEDE B, HIROTA K. On variouseigen fuzzy sets and their application to image reconstruction[J]. Information Sciences,2006,176(20):2988-3010. [5] NOBUHARA H, PEDRYCZ W, SESSA S, et al. A motion compression/reconstruction method based on maxt-norm composite fuzzy relational Equations[J]. Information Sciences,2006,176(17):2526-2552. [6] DI NOLA A, RUSSO C. Lukasiewicz transform and its application to compression and reconstruction of digital images[J]. Information Sciences,2007,177(6):1481-1498. [7] LOETAMONPHONG J, FANG S C. An efficient solution procedure for fuzzy relation equations with max-product composition[J]. IEEE Trans Fuzz Syst,1999,7(4):441-445. [8] PEEVA K, KYOSEV Y. Algorithm for solving max-product fuzzy relational equations[J]. Soft Computing,2007,11(7):593-605. [9] SHIEH B S. Deriving minimal solutions for fuzzy relation equations with max-product composition[J]. Information Sciences,2008,178(19):3766-3774. [10] YANG X P, ZHOU X G, CAO B Y. Single-variable term semi-latticized fuzzy relation geo-metric programming with max-product operator[J]. Information Sciences,2015,325(24):271-287. [11] YANG X P, ZHOU X G, CAO B Y. Latticized linear programming subject to max-product fuzzy relation inequalities with application in wireless communication[J]. Information Sciences,2016,358(17):44-55. [12] YANG X P, ZHOU X G, CAO B Y. Min-max programming problem subject to addition-min fuzzy relation inequalities[J]. IEEE Transactions on Fuzzy Systems,2016,24(1):111-119. [13] 杨吉会,曹炳元. 取大乘积型模糊关系几何规划[J]. 应用数学与计算数学学报,2005,19(2):79-84. [14] 曹炳元. 应用模糊数学与系统[M]. 北京:科学出版社,2005. [15] 胡宝清. 模糊理论基础[M]. 武汉:武汉大学出版社,2004. [16] 杨晓鹏,杨晓斌. 模糊关系方程在实验室点对点网络系统中的应用[J]. 辽宁工程技术大学学报,2016,35(1):79-84. [17] 曾中海,吴莉,王学平. BL-代数上sup-*合成模糊关系方程的极小解与算法[J]. 四川师范大学(自然科学版),2013,36(2):185-89. [18] 王学平. 完备格上模糊关系方程的研究进展[J]. 四川师范大学学报(自然科学版),2009,32(3):365-376. [19] 屈小兵,雷满华. 完备Brouwerian格上模糊关系方程解集的一种分类[J]. 四川师范大学学报(自然科学版),2013,36(2):185-89. [20] 何鹏,王学平. 覆盖矩阵和max-min合成模糊关系方程的极小解[J]. 模糊系统与数学,2015,29(2):109-117.



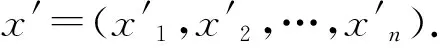








3 模糊关系方程极小解的判别算法







4 结束语

