具有非卷积型核的双线性Littlewood-Paley算子的有界性
2018-04-28周盼,周疆
周 盼, 周 疆
(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)
1 引言及主要结果




定义1.1(非卷积型核) 设K(x,y1,y2)为定义在(Rn)3

(1)
(2)
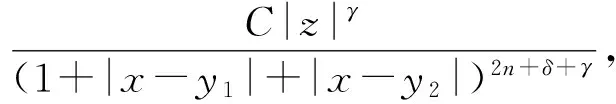
(3)


其中,Γ(x)={(z,t)∈Rn+1+:|z-x|
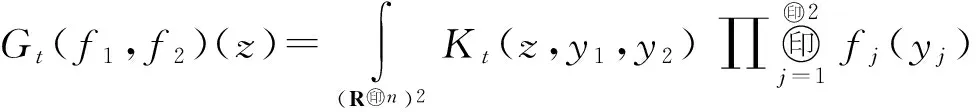
下面介绍Campanato和BMO空间的定义.
定义1.2[20]设1≤p<∞,-n/p≤α<1和f∈Lloc(Rn).如果对于任意的球B⊂Rn,有

定义1.3设f∈Lloc(Rn),如果




‖g(f1,f2)‖BMO(Rn)≤
C‖f1‖Eα1,p1(Rn)‖f2‖Ln/α1(Rn).

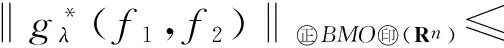
注1.1因为在文献[21]中有如下的点态估计
因此以上的结果对于双线性的Lusin面积积分S也是成立的.
下面给出证明过程中用到的一个主要引理.
引理1.1[22]设f∈Eα,p(Rn),1≤p<∞.如果β>0,-∞<α 其中C是仅仅依赖于n、α、β一个常数. 在定理1.1的证明过程中充分借鉴了文献[18]中的步骤方法.下面给出定理1.1的证明. 定理1.1的证明对于f1∈Eα1,p1(Rn),f2∈Ln/α1(Rn),由文献[18]的定理1.1的思想方法可知,当g(f1,f2)(x0)在一点x0∈Rn处有限,则g(f1,f2)(x)在Rn上几乎处处有限. 现在证明g(f1,f2)的有界性.设 E={x∈Rn:g(f1,f2)(x)<∞}, 仅需证明对于任意的以x0∈E为中心,r为半径的球B=B(x0,r),有 事实上,对于任意的x,y∈B,设r=|x-y|,通过核的条件(1)有 对于I2,由于B(x0,4r)⊂B(y,6r),同样可以得到 对于I3,由核的条件(3)可得 对于I4,注意到 t+|x-y1|+|x-y2|~4r+|x0-y1|+|x0-y2|. 因此,当α1>0,取0<ε<δ-α1,通过引理1.1和核的条件(3)可得 结合以上的估计,对于任意的球B有 至此,完成了定理1.1的证明. 下面给出定理1.2的具体证明过程.首先给出一个注记.对于任意非负整数k,定义 J(k)≡{(z,t)∈Rn+1+:|z-x0|< 仅需要证明对于任意的以x0∈E为中心,r为半径的球B=B(x0,r),有 事实上,对于任意的x,y∈B,设r=|x-y|,通过核的条件(1)有 对于H2,由于B(x0,4r)⊂B(y,6r),同样可以得到 对于H3,由核的条件(2)可得 t+|z-y1|~r+|x0-y1|. 因此通过引理1.1有 对于H4,类似于H3的估计,同样可得 |H4|≤C‖f1‖Eα1,p1(Rn)‖f2‖Ln/α1(Rn). 对于H5,通过核K的条件(2)可以得到 t+|z-y1|+|z-y2|~r+|x0-y1|+|x0-y2|. 因此,当α1≥0时,取0<ε<δ-α1,通过引理1.1可得 对于H6,类似于H5的估计,同样可得 |H6|≤C‖f1‖Eα1,p1(Rn)‖f2‖Ln/α1(Rn). 对于H8,由文献[18]中引理3.2类似可得 类似于H5的估计,可以得到 由对称性,同样可以得到 结合以上的估计,对于任意的球B有 至此,完成了定理1.2的证明. [1] COIFMAN R R, MEYER Y. On commutators of singular integrals and bilinear singular integrals[J]. Trans Am Math Soc,1975,212(10):315-331. [2] GRAFAKOS L, TORRES R H. Multilinear Calderón-Zygmund theory[J]. Adv Math,2002,165(1):124-164. [3] GRAFAKOS L, TORRES R H. Maximal operator and weighted norm inequalities for multilinear singular integrals[J]. Indiana Univ Math J,2002,51(5):1261-1276. [4] COIFMAN R R, MEYER Y. Au-deldes Opérateurs Pseudo-différentiels[M]. Paris:Société Mathématique De France Paris,1978:57. [5] YABUTA K. A multilinearization of Littlewood-Paley’sg-function and Carleson measures[J]. Tohoku Math J,1982,34(2):251-275. [6] SATO S, YABUTA K. Multilinearized Littlewood-Paley operators[J]. Sci Math Jpn,2002,55(3):447-453. [7] HART J. Bilinear square functions and vector-valued Calderón-Zygmund operators[J]. J Fourier Anal Appl,2012,18(6):1291-1313. [8] XUE Q Y, PENG X X, YABUTA K. On the theory of multilinear Littlewood-Paleyg-function[J]. J Math Soc Jpn,2015,67(2):535-559. [9] XUE Q Y, YAN J Q. On multilinear square function and its applications to multilinear Littlewood-Paley operators with non-convolution type kernels[J]. J Math Anal Appl,2015,422(2):1342-1362. [10] WANG S L. Some properties of Littlewood-Paley’sg-functions[J]. Sci Sin,1985,28(3):30-40. [11] 韩永生. 关于S-函数和Marcinkiewicz积分的一些性质[J]. 北京大学学报(自然科学版),1987(5):21-34. [12] WANG S L, CHEN J C. Some notes on square function operators[J]. Chin Ann Math,1990,A11(5):630-638. [13] SUN Y Z. On the existence and boundedness of square function operators on Campanato spaces[J]. Nagoya Math J,2004,173:139-151. [14] 楼煜波,陶祥兴. 参数型Marcinkiewicz积分在广义Campanato空间中的有界性[J]. 宁波大学学报(理工版),2008,21(4):528-532. [15] 吴世旭. 有界核参数型Marcinkiewicz积分交换子的端点估计[J]. 四川师范大学学报(自然科学版),2009,32(2):179-183. [16] 瞿萌,夏珩,束立生. 参数型Marcinkiewicz积分算子的BLO估计[J]. 北京师范大学学报(自然科学版),2010,46(6):664-667. [17] CHEN X, XUE Q Y, YABUTA K. On multilinear Littlewood-Paley operators[J]. Nonlinear Anal,2015,115:25-40. [18] HE S, XUE Q Y, MEI T, et al. Existence and boundedness of multilinear Littlewood-Paley operators on Campanato spaces[J]. J Math Anal Appl,2015,432(1):86-102. [19] WANG D H, ZHOU J. Bilinear Calderón-Zygmund operators on Sobolev, BMO and Lipschitz spaces[J]. J Inequal Appl,2015,391:1-12. [20] DING Y, LU S Z, XUE Q Y. On Marcinkiewicz integral with homogeneous kernels[J]. J Math Anal Appl,2000,245(2):471-488. [21] STEIN E M. On the functions of Littlewood-Paley, Lusin, and Marcinkiewicz[J]. Trans Am Math Soc,1958,88(2):430-466. [22] FABES E B. Spaces of harmonic functions representable by Poisson integrals of functions in BMO and Lp,λ[J]. Indiana Univ Math J,1976,25(2):159-170.
2 定理1.1的证明














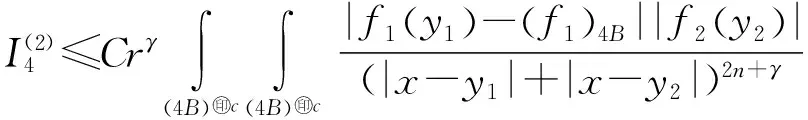

3 定理1.2的证明
2k-2r,0





















