基尔霍夫型吊桥方程指数吸引子的存在性

贾 澜, 马巧珍

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

设Ω⊂R2是具有光滑边界∂Ω的有界开区域,考虑下面的初边值问题

指数吸引子的存在性，其中,p是一个恰当的实数,α>0,β>0,k2u+为恢复力,k2为弹力系数,g∈L2(Ω).方程(1)是文献[1]作为非线性分析的新问题重新提出的.吊桥方程解的渐近行为已被诸多学者研究,可参见文献[2-15]等;文献[2]研究了方程(1)在非自治情形下,即外力项g与时间变量有关时的强全局吸引子的存在性;文献[3]讨论了该方程在强空间中的强解和全局吸引子的存在性;文献[4]得到了非自治吊桥方程的拉回吸引子的存在性;随后,文献[5]证明了带非线性阻尼的吊桥方程全局吸引子的存在性;最近,文献[6]利用Lyapunov函数的方法得到了带有线性记忆的吊桥方程的全局吸引子;文献[7]获得了吊桥方程指数吸引子的存在性.本文继续关注吊桥方程(1)的指数吸引子,从以下2个方面推广和改进文献[7]的结果.首先,从模型上来说,文献[7]中要求p=β=0,而本文中p是一个恰当的实数,且‖▽u‖2Δu是非线性的,这不仅使方程更加广泛,也使一些具体的估计更加复杂.其次,非线性项满足的耗散性条件比文献[7]的弱.

1 泛函集和预备结果

不失一般性,记H=L2(Ω),并赋予一般的内积〈·,·〉和范数‖·‖.更一般地,定义Hr=D(Ar/4),∀r∈R,并赋予其内积为〈u,v〉r=〈Ar/4u,Ar/4v〉.用‖·‖r=‖Ar/4‖表示由上面的内积诱导的Hr的范数.特别地

D(A0)=H,D(A1/2)=V,
D(A)={u∈H4(Ω):u|∂Ω=Δu|∂Ω=0},

其中,A=Δ2,A1/2=-Δ.由紧嵌入Hr+1⊂Hr并结合Poincaré不等式得

(2)

其中λ1>0是A的第一特征值.

为了证明本文的主要结论,假设非线性函数f∈C2(R,R)并且满足下面的条件:

(3)

f′(s)≤C(1+|s|p), ∀p≥1,
s∈R.

(4)

除此以外,还需要下面一些抽象结果.

定义1[8](指数吸引子) 设{S(t)}t≥0为完备度量空间X中的半群,集合M∈X称为半群{S(t)}t≥0的指数吸引子,如果:

(i) 集合M在X中紧且有有限分形维数;

(ii) 集合M为正不变的,即S(t)M⊂M;

(iii) 集合M⊂X为半群{S(t)}t≥0的指数吸引集,即对每一个有界集B∈X,存在常数k=k(B),l>0,使得

dist(S(t),B)≤ke-lt.

定义2[9](加强的平坦性条件) 设X为一致凸的Banach空间,对任意的有界子集B⊂X,存在X的有限维子空间X1⊂X及k、l>0和T>0,使得:

引理1[9]设{S(t)}t≥0为完备度量空间X中的半群,B为{S(t)}t≥0在空间X中的有界吸收集,则以下条件等价:

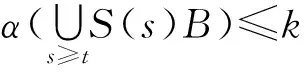
(ii) 半群{S(t)}t≥0在X中拥有指数吸引子.

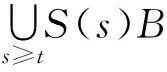
引理3[9]设X为一致凸Banach空间,{S(t)}t≥0为X中的强连续或强弱连续半群,则{S(t)}t≥0在X中拥有指数吸引子,如果满足:

(i) {S(t)}t≥0在X中存在有界吸收集B⊂X,

(ii) {S(t)}t≥0满足加强的平坦性条件.

引理4[10-11]假设条件(3)和(4)成立,p∈R,α>0,β>0,若g∈L2(Ω),u1∈V，u2∈H,则问题(1)存在唯一解u满足

u∈C([0,T],V),
ut∈C([0,T],H), ∀T≥0,

并且{u1,u2}→{u(t),ut(t)}在V×H上连续.

利用引理4,可以定义与问题(1)相关的C0半群S(t),即

S(t):{u1,u2}→{u(t),ut(t)},t≥0,

且S(t)将V×H映射到它本身.

2 指数吸引子的存在性

由引理3,为了证明指数吸引子的存在性,首先需要下面的结论.

定理1(有界吸收集) 设p∈R,α>0,β>0,g∈L2(Ω),f∈C2(R;R)满足(3)和(4)式,则与问题(1)相关的解半群S(t)在V×H中存在有界吸收集.

证明选取0<ε<1,用v=ut+εu在H和方程(1)做内积得

(5)

利用Poincaré不等式、Hölder不等式及Young不等式可得

(6)

另外

(7)

并且

(8)

将(6)～(8)式代入(5)式得

(9)

令

(10)

(11)

有

(12)

则

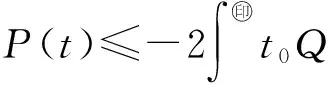
(13)

其中

P(0)=‖Δu1‖2+‖u2+εu1‖2-
p‖u1‖4+k2‖u+1‖2+
ddx.

(14)

由条件(3)和F(u)的定义知,存在2个正常数K1、K2及η=η(ε)>0使得

f(s)s+ηs2+K1≥0, ∀s∈R,

(15)

F(s)+ηs2+K2≥0, ∀s∈R.

(16)

结合(2)、(9)～(11)、(15)～(16)式及Young不等式有

(17)

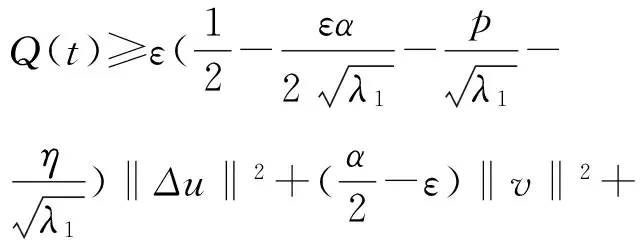
(18)

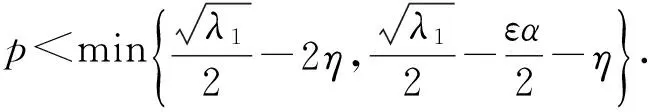
P(t)≥C1(‖Δu‖2+‖v‖2+
‖▽u‖4+‖u+‖2)-M1,
Q(t)≥C1(‖Δu‖2+‖v‖2+
‖▽u‖4+‖u+‖2)-M2,

(19)

由(13)和(19)式可得

(20)

‖Δu(t0)‖2+‖v(t0)‖2+‖▽u(t0)‖4+
‖u+(t0)‖2≤K.

(21)

则B0是半群{S(t)}t≥0的有界吸收集.

引理5[9]设p∈R,α>0,β>0,f∈C2(R;R)满足(3)和(4)式,则f:H2(Ω)→H1,p(Ω),∀p≥1为紧连续.

定理2设p∈R,α>0,β>0,g∈L2(Ω),f∈C2(R;R)满足(3)和(4)式,则与问题(1)对应的解半群S(t)在V×H中满足加强的平坦性条件.

证明设λj,j=1,2,…,n为算子A在空间H中的特征值,满足0<λ1<λ2≤…≤λj≤…,且当j→∞时,λj→∞;ωj为特征值λj对应的特征向量,它们构成空间H的一组正交基,同时也是空间V的正交基,满足Aωj=λjωj,∀j∈N.

设Hm=span{ω1,ω2,…,ωm},Pm:H→Hm为正交投影.对∀(u,ut)∈V×H,作如下分解(u,ut)=(u1,u1t)+(u2,u2t),其中(u1,u1t)=(Pmu,Pmut).

选取0<ε<1,且0<ε(α-ε)<λ1.用v2(t)=u2t(t)+εu2(t)作为试验函数与(1)式在空间H中作内积,计算得

(22)

由于

〈f(u),v2〉≤(α-ε)/4‖v2‖2+
(α-ε)-1‖(I-Pm)f(u)‖2,

(23)

〈g(x),v2〉≤(α-ε)/4‖v2‖2+
(α-ε)-1‖(I-Pm)g(x)‖2,

(24)

(α-ε)‖v2‖2-ε(α-ε)〈u2,v2〉≥
(α-ε-α2ε/2λ1)‖v2‖2-ε/2‖Δu2‖2,

(25)

所以,结合(22)～(25)式,根据(4)式可得

(26)

定义泛函

则利用(2)式即得

这样,由(26)式可得

(27)

(28)

(29)

所以,当t≥t1时,有

(30)

根据Gronwall引理,可得

(31)

再结合

其中C是与p、λ1、ε有关的恰当的正常数,即得

因此,问题(1)的解半群{S(t)}t≥0在空间V×H中满足加强的平坦性条件.

于是,由引理3、定理1和定理2即得如下的主要结论.

定理3(指数吸引子) 设p∈R,α>0,β>0,g∈L2(Ω),f∈C2(R,R)满足(3)和(4)式,则与问题(1)的相关的解半群{S(t)}t≥0在空间V×H中拥有指数吸引子.

[1] LAZER A C, MCKENNA P J. Large-amplitude periodic oscillations in suspension bridges:some new connection with nonlinear analysis[J]. SIAM Rev,1990,32(4):537-578.

[2] 马巧珍,周富敏. 具有双非线性项的吊桥方程一致吸引子的存在性[J]. 西北师范大学学报(自然科学版),2013,49(5):7-9.

[3] MA Q Z, ZHONG C K. Existence of strong solutions and attractors for the coupled suspension bridge equations[J]. J Diff Eqns,2009,246(10):3755-3775.

[4] PARK J Y, KANG J R. Pullback D-attractors for non-autonomous suspension bridge equation[J]. Nonlinear Anal,2009,71(10):4618-4623.

[5] PARK J Y, KANG J R. Global attractor for suspension bridge equation with nonlinear damping [J]. Quart Appl Math,2011,69(3):465-475.

[6] KANG J R. Pullback attractor for the non-autonomous coupled suspension bridge equations[J]. Appl Math Comput,2013,219(16):8747-8758.

[7] 汪璇,马群,马巧珍. 吊桥方程指数吸引子的存在性[J]. 西北师范大学学报(自然科学版),2015,51(5):4-8.

[8] EDEN A, FOIAS C, NICOLAEKO B, et al. Exponential Attractors for Dissipative Evolution Equations[M]. Chichester:John Wiley & Sons,1994.

[9] LI Y, WU H, ZHAO T. Necessary and sufficient conditions for the existence of exponential attractors for semigroups and applications[J]. Nonlinear Anal,2012,75(17):6297-6305.

[10] ZHONG C K, MA Q Z, SUN C Y. Existence of strong solutions and global attractors for the suspension bridge equations[J]. Nonlinear Anal,2007,67(2):442-454.

[11] TEMAM R. Infinite-dimensional Dynamical Systems in Mechanics and Physics[M]. New York:Springer-Verlag,1997.

[12] BOCHICCHIO I, GIORGI C, VUK E. Long-term damped dynamics of the extensible suspensions bridge[J]. Inter J Diff Eqns,2010(2010):383420.

[13] MA Q Z. Existence of uniform attractors for the nonautononous suspension bridge equations with strong damped[J]. J Math Research Exposition,2010,30(2):277-285.

[14] MA Q Z, WANG S P, CHEN X B. Uniform compact attractors for the coupled suspension bridge equations[J]. Appl Math Comput,2011,217(16):6604-6615.

[15] KANG J R. Long-time behavior of a suspension bridge equation with past history[J]. Appl Math Comput,2015,265(C): 509-519.