局部临界周期分岔的若干进展
2018-04-28陈兴武
陈兴武
(四川大学 数学学院, 四川 成都 610064)
1 引言及基本理论
平面中心型微分系统

(1)
的研究一直是微分方程定性理论及分岔理论(见文献[1-2])的研究热点,这里x,y∈R,P(x,y)和Q(x,y)是解析函数且P(0,0)=Q(0,0)=0.由经典结果[2],系统(1)的平衡点O:(0,0)要么是中心,要么是焦点.此时的中心也称为细中心,焦点也称为细焦点.所以,系统(1)的平衡点O也被称为中心- 焦点.经典的中心问题就是判定中心-焦点O在什么样的参数条件下是中心.这是对平衡点类型的判定.
在分岔方面,系统(1)常常发生的Hopf分岔吸引了国内外众多学者的关注.Hopf分岔是指当参数发生微小变化时,在系统(1) 的平衡点O充分小邻域内产生出极限环的现象.这属于传统分岔研究中的一种,即在参数微小变化下微分系统相图的拓扑结构发生变化.Hopf分岔与著名的希尔伯特第16问题有密切关系.迄今,系统(1) 在Hopf分岔的研究方面已有了丰富结果.而且,大部分的结果都是针对系统(1)的平衡点O是细焦点的情形,有少量结果是针对细中心的情形[3].对细中心的情形,系统(1)还存在另外一种分岔.这就是本文主要介绍的局部临界周期分岔.
当平衡点O是系统(1)的细中心时,在相平面中围绕O的是一族周期轨道.根据这族周期轨道中每条轨道的最小正周期,可以定义一个周期值函数.具体地,令Γ(r)是系统(1)的相平面内周期轨道族中经过点(r,0)的周期轨道,其中0 其中,所有pi(λ)是解析函数且满足在收敛幂级数环R{λ}中 p2k+1∈(p2,p4,…,p2k), 其中,(p2,p4,…,p2k)是p2,p4,…,p2k在收敛幂级数环R{λ}中生成的理想.所以,p2k称为第k阶周期量. 由于周期值函数P(r,λ)的单调性等性质对系统(1)的定性分析和分岔研究极其重要,国内外众多学者非常关注周期值函数P(r,λ)的研究.如果对所有充分小的r,周期值函数P(r,λ)恒为常数,也即所有阶周期量都为0,则称细中心O为等时中心.可见,等时中心是被一族具有相同最小正周期的周期轨道围绕.判定细中心在什么样的参数条件下是等时中心就是所谓的等时中心问题.如果O不是等时中心,则一定存在一个非负整数κ,使得 p0(λ)=…=p2κ(λ)=0,p2κ+2(λ)≠0, 这里p0(λ)定义为零函数.此时,称O为κ重细中心.有时也称等时中心为无穷重细中心. 周期值函数P(r,λ)的临界点对应的周期值称为临界周期.给定参数值λ*∈Rm,如果对任意的>0及λ*的任意小邻域W,存在点λ1∈W使得方程P′(ξ,λ1)=0在(0,)中有k个解,则称k个局部临界周期从对应于参数值λ*的细中心分岔出来.与传统的分岔相区别的是:局部临界周期分岔并不改变系统相空间内的相图拓扑结构,仅仅是周期值函数的性质发生变化. Chicone等[4]于1989年建立了局部临界周期分岔的基本理论. 引理1.1[4]假设λ=λ*时,系统(1)的平衡点O是一个k重细中心,则至多k个局部临界周期从O分岔出来. 由引理1.1知,细中心的重数是其分岔出局部临界周期个数的一个上界.但是,这个上界是否可达还是未知.为了确定这个可达性,首先需要介绍如下无关性定义. 定义1.1[4]对一族连续函数fi:RN→R,i=1,…,l,如果 3) 满足f1(μ″)=0,f2(μ″)≠0的点μ″的任意小邻域内有点μ‴,使得f1(μ‴)f2(μ″)<0; 则称f1,…,fl-1在μ*处与fl是无关的. 特别地,如果函数f1,…,fl是连续可导的,则根据定义1.1不难推导出:l个向量▽f1(μ*),…,▽fl(μ*)线性无关蕴含f1,…,fl-1在μ*处与fl是无关的,其中▽fi(μ*)表示μ*处的梯度向量.但反之不成立,即f1,…,fl-1在μ*处与fl无关不能导出向量▽f1(μ*),…,▽fl(μ*)线性无关.有了无关性定义,可以给出如下2个局部临界周期分岔的基本定理. 定理1.1[4](有限重分岔定理)假设λ=λ*时,系统(1)的平衡点O是一个k重细中心,则至多k个局部临界周期从O分岔出来.进一步,如果周期量p2,p4…,p2k在λ*处与p2k+2是无关的,则存在λ*附近的扰动,使得恰有j(j≤k) 个局部临界周期分岔出来. 定理1.2[4](等时分岔定理)假设λ=λ*时,系统(1)的平衡点O是一个等时中心,且所有周期量都属于p2,…,p2k+2在R{λ}λ*中生成的理想.其中R{λ}λ*是在λ*处收敛的幂级数环,则至多k个局部临界周期从O分岔出来.进一步,如果周期量p2,p4…,p2k在λ*处与p2k+2是无关的,则存在λ*附近的扰动,使得恰有j(j≤k)个局部临界周期分岔出来. 自1989年Chicone等[4]建立局部临界周期分岔的基本理论以来,局部临界周期分岔越来越受到关注.而近十年来多项式代数及符号计算的发展更是极大地推动了局部临界周期分岔的研究.本文将围绕二次及三次多项式微分系统、Liénard系统、非多项式微分系统及刚性中心系统等,介绍局部临界周期的若干结果及最新发展. 当P(x,y)、Q(x,y)是二次齐次多项式时,系统(1)是二次多项式微分系统.由文献[5],任何具有围绕O的周期轨道的二次系统都可以经过坐标线性变换而化为Bautin系统 (2) 其中(λ1,…,λ6)∈R6.局部临界周期分岔是在细中心的情形下考虑的.所以,限定λ1=0且(λ2,…,λ6)位于中心簇内,即 其中 B1:={(λ2,…,λ6)∈R5:λ4=λ5=0}, B2:={(λ2,…,λ6)∈R5:λ3=λ6}, B3:={(λ2,…,λ6)∈R5:λ5= λ4+5λ3-5λ6=λ3λ6-2λ62-λ22=0}, B4:={(λ2,…,λ6)∈R5:λ2=λ5=0}. 在中心簇的基础上,Loud于1964年给出了Bautin系统(2)的等时中心条件和有限重细中心的最大重数. 定理2.1[6]当Bautin系统(2)的平衡点O是有限重细中心时,其重数不超过2.Bautin系统(2)的平衡点O是等时中心当且仅当λ1=0且要么(λ2,…,λ6)=(0,…,0),要么经过坐标线性变换原系统化为Loud系统 其中(F,D)=(1,0)或(2,-1/2)或(1/4,0)或(1/2,-1/2).具体地,Bautin系统(2)的平衡点O是等时中心当且仅当λ1=0且 其中 B1:={(λ2,…,λ6)∈R5:λ3-λ6= λ4+4λ3=λ5+4λ2=0}, B2:={(λ2,…,λ6)∈R5:λ2=λ5= λ6=λ4+3λ3=0}, B3:={(λ2,…,λ6)∈R5:λ2=λ5= λ6=λ4+6λ3=0}, B4:={(λ2,…,λ6)∈R5:λ2=λ5= λ3-4λ6=λ4+10λ6=0}. 通过对有限重细中心及定理2.1中给出的等时中心进行扰动分析,Chicone等[4]给出了二次多项式微分系统局部临界周期分岔结果: 定理2.2[4]1) 如果二次多项式微分系统的平衡点O是一个有限重细中心,则至多2个局部临界周期分岔出来.而且,存在参数扰动使得恰有j(j=1,2)个局部临界周期分岔出来. 2) 从非线性的二次系统的等时中心至多分岔出1个局部临界周期;线性等时中心在二次系统族中扰动时,至多2个局部临界周期分岔出来.并且,这两种情况的最大个数1和2 都是可达的. 从上一章可见,二次多项式微分系统的局部临界周期分岔已研究完整.然而,虽然三次多项式微分系统局部临界周期分岔的研究吸引了众多学者,但由于其中心问题至今都没有得到完全解决,其局部临界周期分岔仅对某些特殊的三次系统有研究结果.一般三次系统的局部临界周期分岔问题还没得到完全解决.在本章中,将对现有的三次系统的局部临界周期分岔结果作介绍.1991年,李继彬等[7]考虑了 (3) 即系统(1)中的P、Q为三次齐次多项式.他们给出了有限重细中心局部临界分岔的结果,证明了存在参数扰动使得2个局部临界周期分岔出来.紧接着,Rousseau等[9]继续考虑系统(3)在Sibirskii形式下的情形,即 a30:=A1-A2-A3,a21:=3A4-A6, a12:=3A2+A7-3A3-2A1, a03:=A5-A4, b30:=A4+A5, b21:=3A3+2A2+2A1, b12:=A6-A3, b03:=A3-A2-A1. 注意,Sibirskii形式下的齐三次系统与系统(3)是等价的.写为Sibirskii形式更为方便表示中心条件: 定理3.1[8]系统(3)的平衡点O是细中心当且仅当λ:=(A1,…,A7)∈S1∪S2∪S3,其中 S1:={λ:A1=A7=0}, S2:={λ:A3=A5=A6=A7= 4(A42+A22)-A12=0}, S3:={λ:A2=A5=A7=0}. 当λ∈S1(S2,S3)时,称O是系统(3) 的第I(II,III)类细中心.通过对这3类细中心的分析,Rousseau等[9]证明了如下定理: 定理3.2[9]至多3个局部临界周期从系统(3)的有限重细中心或线性等时中心O分岔出来;至多2个局部临界周期从系统(3)的非线性等时中心O分岔出来.而且,这2种情况的上界3和2都是可达的. 上面齐三次系统(3)是实系统的形式.2003年,Romanovski和Han[10]考虑了齐三次系统的复形式也证明了定理3.2中关于等时中心分岔出临界周期的结果. 对非齐次的三次系统,首先考虑约化Kukles系统 (4) 系统(4)的中心条件在下面定理中给出. 定理3.3[11]系统(4)的平衡点O是细中心当且仅当λ:=(a1,…,a6)∈K1∪K2∪K3∪K4,其中 K1:={λ:a4=a5=a6=a1+a3=0}, K2:={λ:a4+a3(a1+a3)= a5-a2(a1+a3)= a6(a1+2a3)-a32(a1+a3)=0}, K3:={λ:a2=a5=0}, K4:={λ:a1=a3=a5=0}. 在此基础上,1997年Rousseau等[12]解决了系统(4)的等时中心问题和局部临界周期分岔问题. 定理3.4[12]系统(4)的平衡点O是等时中心当且仅当 a1=a3=5=a6=a22-9a4=0. 定理3.5[12]1) 若λ∈K1,则系统(4)的细中心O是0重细中心,且无局部临界周期从此细中心分岔出来; 2) 若λ∈K2K1,则系统(4)的细中心O的重数至多为2,且存在扰动使得恰有j(j≤2)个局部临界周期从2重细中心分岔出来; 3) 若λ∈K3,则系统(4)的细中心O的重数至多为3,且存在扰动使得恰有j(j≤3)个局部临界周期从3重细中心分岔出来; 4) 若λ∈K4,则系统(4)的细中心O的重数不大于2或为非线性等时中心,且存在扰动使得恰有j(j≤2)个局部临界周期从2重细中心分岔出来. 定理3.6[12]1) 至多1个局部临界周期从系统(4)的非线性等时中心O分岔出来,且存在产生1个局部临界周期的扰动; 2) 至多3个局部临界周期从系统(4)的线性等时中心O分岔出来.特别地,没有局部临界周期从K1中的扰动产生;至多2(3)个局部临界周期从K2K4(K3K4)中的扰动产生;至多2个局部临界周期从K4中的扰动产生,且存在恰好产生2个局部临界周期的扰动. 三次可逆系统 (5) 是非常重要的一类具有中心O的三次系统,得到了广泛关注.当系统(5)的对应二次系统是等时中心时,把系统(5)看作二次等时中心系统的扰动.由定理2.1知,此二次等时中心系统有4种情况.Zhang等[13]于2000年考虑了第4种情况,即系统 (6) 他们借助符号计算给出了其等时中心条件并证明了有限重细中心的最大重数是4.进一步,他们证明了如下定理. 定理3.7[13]对给定的k=1,2,…,4,系统的k重细中心分岔出至多k个局部临界周期,且存在产生j(j≤k)个局部临界周期的扰动. 2009年,Chen和Zhang[14]继续考虑了三次可逆系统的临界周期分岔问题.通过对剩余的3种情况逐一分析,在有限重细中心局部临界分岔方面得到了和定理3.7一样的结果.而且,对第一种情况的系统 (7) 证明了如下等时中心局部临界周期分岔的结果. 定理3.8[14]系统(7)的等时中心分岔出至多3个局部临界周期,且存在产生j(j≤3)个局部临界周期的扰动. 其他类型的三次系统的局部临界周期分岔也有一些结果,比如:2013年Chen等[15]考虑三次Kolmogorov系统 (8) 的中心问题及局部临界周期分岔,给出了中心、等时中心条件,证明了至多2个局部临界周期从系统(8)的有限重细中心或等时中心(a,b)分岔出来,且这2种情形下上界2都是可达的.陈挺等[16]和Huang等[17]分别研究了如下特殊三次系统 (9) 和一个Z2对称三次系统 的局部临界周期分岔,证明了至多3个局部临界周期从系统(9)或系统(10)的有限重细中心分岔出来,而且上界3是可达的. 2015年,Fercec等[18]把实系统的临界周期分岔理论化为复系统的对应理论,并利用计算机代数系统分别证明了至多3、2、3个局部临界周期从下面3个特殊系统(复系统形式)分岔出来: 其中u∈C. 最近,Romanovski等[19]研究了广义Riccati系统 (11) 的中心问题、等时中心问题、全局结构及有限重细中心的局部临界周期分岔.他们给出了6类非线性情形的中心条件I1,…,I6,并对每一类细中心给出了如下分岔定理. 定理3.9[19]当中心条件I1(I2,…,I6)成立且系统(11)的细中心O的重数为有限重时,则其重数至多为3(0,0,3,2,2),且存在扰动使得3(0,0,3,2,2)个局部临界周期从3(0,0,3,2,2)重细中心分岔出来. 本章介绍Liénard系统的局部临界周期分岔进展.首先考虑无阻尼(保守)的Liénard系统 (12) 其中g(x)是多项式函数且使得O是细中心.显然,系统(12)是一个哈密尔顿系统,其能量函数为 H(x,y):=y2/2+G(x), 定理4.1[4]如果 则至多n-2个局部临界周期从系统(12)的细中心O分岔出来.而且,存在参数扰动使得恰有j(j≤n-2)个局部临界周期分岔出来. 定理4.2[4]1) 如果 则至多1个局部临界周期从系统(12)的细中心O分岔出来.而且,存在参数扰动使得恰有1个局部临界周期分岔出来. 2) 如果 则至多2个局部临界周期从系统(12)的细中心O分岔出来.而且,存在参数扰动使得恰有j(j≤2)个局部临界周期分岔出来. 3) 如果 则至多4个局部临界周期从系统(12)的细中心O分岔出来.而且,存在参数扰动使得恰有j(j≤3)个局部临界周期分岔出来. 从定理4.2可见,当G(x)是一个6次多项式函数时,局部临界周期分岔出的临界周期个数上界是4.但是,此定理只能给出3是可达,但4是否可达仍然是未解决的一个问题. 在保守系统方面,陈兴武等[20]于2009年考虑了一类n-1次的哈密尔顿系统 (13) 其中哈密尔顿函数 他们证明了如下局部临界周期分岔结果. 定理4.3[20]从系统(13)的细中心O至多分岔出m-1个局部临界周期.而且,存在参数扰动使得恰有j(j≤m-1)个局部临界周期分岔出来. 对有阻尼的Liénard系统,Zou等[21]在2008年考虑了系统 (14) 给出了如下结果: 定理4.4[21]系统(14)的平衡点O是一个细中心当且仅当a2=b2=0或a2-a1b2=a3-a1b3=0;系统(14)的平衡点O是一个等时中心当且仅当a2=a3=b2=9b3-a12=0.而且,当O为有限重细中心时,其重数至多为2. 基于定理4.4中的中心条件及重数结果,可以得到如下局部临界分岔定理. 定理4.5[21]1) 对每个k=1,2,至多k个局部临界周期从系统(14)的k重细中心O分岔出来.而且,存在参数扰动使得恰有j(j≤k)个局部临界周期分岔出来. 2) 从系统(14)的线性等时中心O至多分岔出2个局部临界周期.而且,存在参数扰动使得恰有j(j≤2)个局部临界周期分岔出来. 3) 从系统(14)的非线性等时中心O至多分岔出1个局部临界周期.而且,存在参数扰动使得恰有1个局部临界周期分岔出来. 2011年,对比系统(14)次数更高的Liénard系统 (15) Huang等[22]给出了其中心条件、等时中心条件及细中心重数,并分析了有限重细中心的局部临界周期分岔. 定理4.6[22]系统(15)的有限重细中心O的重数至多为2.对每个k=1,2,至多k个局部临界周期分岔出来.而且,存在参数扰动使得恰有j(j≤k)个局部临界周期分岔出来. 对次数更高的Liénard系统 Li[23]于2012年给出了其中心条件、等时中心条件并证明了存在三重细中心.在此基础上,给出了等时中心和某些二重细中心的局部临界周期分岔,证明了可以从二重细中心或等时中心分岔出2个局部临界周期. 上面几章的局部临界周期分岔针对的对象都是多项式微分系统.本章介绍2类非多项式的解析微分系统的局部临界周期分岔. 广义Lotka-Volterra系统 定理5.1[25]系统(17)的有限重细中心O的重数至多为2.对每个k=1,2,至多k个局部临界周期分岔出来.而且,存在参数扰动使得恰有j(j≤k)个局部临界周期分岔出来. 定理5.2[25]当p=q=1/2时,系统(17)的细中心O是等时中心.进一步,对μ=1的情形,至多2个局部临界周期分岔从等时中心分岔出来,且存在参数扰动使得恰有j(j≤2)个局部临界周期分岔出来;对μ≠1的情形,至多1个局部临界周期分岔从等时中心分岔出来,且存在参数扰动使得恰有1个局部临界周期分岔出来. 2013年,Huang等[26]考虑了一类有理系统 (18) 的无穷远平衡点.首先通过变换,他们把系统(18)的无穷远平衡点转换到一个7次多项式系统的原点,并最终给出了系统(18)的无穷远点为有限重细中心的2类条件(C1)和(C2).当条件(C1)成立时,证明了细中心重数要么为0要么为2,且在局部临界周期分岔中这个上界2是可达的;当条件(C2)成立时,证明了细中心重数至多为3.此时,至多k(k≤3)个局部临界周期分岔从k重细中心分岔出来,且存在参数扰动使得恰有j(j≤k)个局部临界周期分岔出来. 考虑系统 (19) 其中Ti(r)称为第i阶周期分岔函数.如果 T1(r)≡…≡Tk-1(r)≡0,Tk(r)≢0, 称周期值函数P(r)是k阶退化的.各阶周期分岔函数的性态可以帮助获得周期值函数P(r)的临界点信息.具体地,如果P(r)是k阶退化的,r*是Tk(r)的一个简单零点,则存在唯一一个满足 r*()→r*,→0 的临界点r*().由于这个临界点r*()是在r*的小邻域中,而不一定是在0附近,所以这时的临界周期分岔发生在周期环域里面,而不一定是前几节说的原点附近. 2008年Cima等[27]研究了线性刚性等时中心的扰动系统 对满足这个形式的可逆系统、哈密尔顿系统、Liénard系统等几类特殊系统给出了临界周期分岔的结果.紧接着,Gasull等[28]考虑了二次等时中心的扰动系统 (20) 其中(D,F)=(0,1),(0,1/4),(-1/2,1/2)或(-1/2,2).他们证明了如下临界周期分岔结果. 定理6.1[28]在1阶退化情形下,至多1个临界周期从系统(20)的周期环域里分岔出来,且存在参数扰动使得恰有1个临界周期分岔出来. 继续针对二次等时中心的情形,Gasull和Zhao[29]考虑了二次刚性等时中心的扰动系统 (21) 和 (22) 定理6.2[29]在1(2或3)阶退化情形下,至多1个临界周期从系统(21)的周期环域里分岔出来,且存在参数扰动使得恰有1个临界周期分岔出来. 定理6.3[29]在1阶退化情形下,至多1个临界周期从系统(22)的周期环域里分岔出来,且存在参数扰动使得恰有1个临界周期分岔出来. 2011年,Chen等[30]考虑了n次齐次刚性等时中心在m次多项式扰动下的系统 (23) 其中 为了研究临界周期分岔,他们给出了系统(22)的第1和第2阶周期分岔函数的积分表达式.特别地,当(n,m)=(3,3)时,系统(22)经过一个坐标线性变换可化为 (24) 其中a=±1. 定理6.4[30]假设a=1(a=-1). 2) 系统(24)的周期环域内至多2个临界周期,且存在参数扰动使得恰有2个临界周期分岔出来. 2013年,Zhou等[31]在小参数的基础上引入了另一个小参数λ,考虑了系统 和 给出了如下结果. 定理6.5[31]在1阶退化情形下,系统(25)和系统(28)都存在参数扰动使得恰有3个临界周期分岔出来. 2014年,Han等[32]对系统 (27) 给出了如下定理. 定理6.6[32]1) 当n=2时,系统(27)在1阶或2阶退化情形下至多分岔出1个临界周期,在3阶退化下为等时系统. 2) 当n=3时,系统(27)在1阶退化情形下至多分岔出1个临界周期,在2阶退化下至多分岔出5个临界周期,在3阶退化下为等时系统. 3) 当n≥2时,系统(27)在1阶退化情形下至多分岔出2[n/2]-1个临界周期;当n≥3时,系统(27)在2阶退化情形下至多分岔出3n-2[(n+2)/2]个临界周期. 对系统 (28) Peng等[33]给出了临界周期分岔结果. 定理6.7[33]1) 系统(28)在1阶或2阶退化情形下至多分岔出2个临界周期,而且这个上界2是可达的. 2) 系统(28)在3阶退化情形下至多分岔出6个临界周期. 3) 当a40()≡a22()≡a04()≡b31()≡b13()≡0时,系统(28)在任意阶退化情形下至多分岔出2个临界周期,而且这个上界2是可达的. 受文献[31-32]的启发,Han等[34]考虑了系统 (29) 和 其中 他们证明了如下临界周期分岔定理. 定理6.8[34]1) 当n=k=2时,存在参数扰动使得系统(29)在1阶退化情形下恰好有1个临界周期. 2) 当n=2,k=3时,存在参数扰动使得系统(29)在1阶退化情形下恰好有2个临界周期. 定理6.9[34]1) 当n=k=2或n=2,k=3时,存在参数扰动使得系统(30)在1阶退化情形下恰好有2个临界周期. 2) 当n=2,k=4时,存在参数扰动使得系统(30)在1阶退化情形下恰好有4个临界周期. 3) 当n=k=3或n=3,k=4时,存在参数扰动使得系统(30)在1阶退化情形下恰好有5个临界周期. 2016年,Lu等[35]首先把系统(28)的临界周期分岔结果从定理6.7的结论1中描述的“在1阶或2阶退化情形下至多分岔出2个临界周期,而且这个上界2是可达的”推进到“在任意阶退化情形下至多分岔出2个临界周期,而且这个上界2是可达的”.然后,他们考虑了系统 给出了如下结果: 定理6.10[35]1) 当n=1时,系统(31)在1阶退化情形下至多分岔出2个临界周期,而且这个上界2是可达的. 2) 当n≥2时,系统(31)在1阶退化情形下至多分岔出3n-1个临界周期. 紧接着,Peng等[36]于2017年对系统 (32) 给出了如下结果: 定理6.11[36]1) 当n=3或4时,系统(32)在1阶退化情形下至多分岔出2个临界周期,而且这个上界2是可达的. 2) 当n=5时,系统(32)在1阶退化情形下至多分岔出4个临界周期,而且这个上界4是可达的. 3) 当n≥6时,系统(32)在1阶退化情形下至多分岔出2[(n-1)/2]个临界周期. 在前面几章中,较为详细地介绍了临界周期分岔的大量研究结果.从技术上来讲,临界周期分岔主要需要对各阶周期量进行分析,包括计算它们的代数簇、判断它们之间的无关性以及确定它们在收敛幂级数环中生成理想的有限生成元等.从研究难度来讲,临界周期分岔与熟知的Hopf分岔是相当的.而其中最为困难的从等时中心分岔出临界周期更是相当于从细中心分岔出极限环的研究难度.最根本的就是涉及到确定有限生成元的问题.这本身在代数上也是相当困难的一件事,而且没有一般高效的方法.这就是等时中心分岔出临界周期结论偏少的根本原因.已有的等时中心分岔出临界周期的结果主要集中在刚性系统.从研究的系统来讲,目前主要针对低次的多项式微分系统和较为特殊的高次系统.这主要是涉及到的大量符号计算所导致的.随着计算机代数系统的发展,人们渐渐可以处理较多参数的符号计算,这使得越来越多的高次系统的临界周期分岔被完整解决或部分解决.但是,总体上来讲,临界周期分岔的研究方法还没有大的突破.比如,在判断分岔出的临界周期个数上界是否可达的时候往往需要判断周期量的无关性,而无光性方法仅仅是判定上界可达与否的一个充分性的判定方法.方法的欠缺使得极大地依赖符号计算.所以,临界周期分岔的发展急需新的方法. [1]CHOWSN,HALEJK.MethodsofBifurcationTheory[M].NewYork:Springer-Verlag,1982. [2]ZHANGZ,DINGT,HUANGW,etal.Qualitativetheoryofdifferentialequations[C]//TranslMathMonogr.ProvidenceRI:AmMathSoc,1992. [3]CHRISTOPHERC,LIC.LimitCyclesofDifferentialEquations[M].Basel:Birkhäuser,2007. [4]CHICONEC,JACOBSM.Bifurcationofcriticalperiodsforplanevectorfields[J].TransAmMathSoc,1989,312(2):433-486. [5]BAUTINNN.Onthenumberoflimitcycleswhichappearwiththevariationofcoefficientsfromanequilibriumpositionoffocusorcentertype[J].AmMathSocTransl,1954,100:1-19. [6]LOUDWS.Behavioroftheperiodofsolutionsofcertainplaneautonomoussystemsnearcenters[J].ContrDiffEqns,1964,3:21-36. [7] 林怡平,李继彬. 平面自治系统的规范型与闭轨族周期的临界点[J]. 数学学报,1991,34(4):490-501. [8]MALKINKE.Criteriaforcenterforadifferentialequation[J].VolzhskiiMatemSbornik,1964,2:87-91. [9]ROUSSEAUR,TONIB.Localbifurcationofcriticalperiodsinvectorfieldswithhomogeneousnonlinearitiesofthethirddegree[J].CanadMathBull,1993,36(4):473-484. [10]ROMANOVSKIVG,HANMA.Criticalperiodbifurcationsofacubicsystem[J].JPhys:MathGen,2003,A36(18):5011-5022. [11]CHRISTOPHERC,LLOYDNG.OnthepaperofJinandWangconcerningtheconditionsforacentreincertaincubicsystems[J].BullLondonMathSoc,1990,22(1):5-12. [12]ROUSSEAUR,TONIB.LocalbifurcationsofcriticalperiodsinthereducedKuklessystem[J].CanJMath,1997,49(49):338-358. [13]ZHANGWN,HOUXR,ZENGZB.Weakcentersandbifurcationofcriticalperiodsinreversiblecubicsystems[J].ComputMathAppl,2000,40(6):771-782. [14]CHENXW,ZHANGWN.Decompositionofalgebraicsetsandapplicationstoweakcentersofcubicsystems[J].JComputApplMath,2009,232(2):565-581. [15]CHENXW,HUANGWT,ROMANOVSKIVG,etal.LinearizabilityandlocalbifurcationofcriticalperiodsinacubicKolmogorovsystem[J].JComputApplMath,2013,245(6):86-96. [16] 陈挺,黄文韬,马皖川. 一类三次系统的细中心与局部临界周期分支[J]. 中北大学学报(自然科学版),2014,35(5):499-503. [17]CHENT,HUANGWT,RENDC.WeakcentersandlocalcriticalperiodsforaZ2-equivariantcubicsystem[J].NonlinearDyn,2014,78(4):2319-2329. [18]FERCECB,LEVANDOVSKYYV,ROMANOVSKIVG,etal.Bifurcationofcriticalperiodsofpolynomialsystems[J].JDiffEqns,2015,259(8):3825-3853. [19]ROMANOVSKIVG,FERNANDESW,TANGYL,etal.Linearizabilityandcriticalperiodbifurcationsofageneralizedriccatisystem[J].NonlinearDynamics,2017,90(1):257-269. [20] 陈兴武,李燕,邹兰. 2n-1次Hamilton系统的临界周期分岔[J]. 四川大学学报(自然科学版),2009,46(1):11-14. [21]ZOUL,CHENXW,ZHANGWN.LocalbifurcationsofcriticalperiodsforcubicLienardequationswithcubicdamping[J].JComputApplMath,2008,222(2):404-410. [22]XUQJ,HUANGWT.ThecenterconditionsandlocalbifurcationofcriticalperiodsforaLienardsystem[J].ApplMathComput,2011,217:6637-6643. [23]LIHW.LocalbifurcationsofcriticalperiodsforquarticLienardequationswithquinticdamping[J].AdvDifferenceEqns,2012,2012:24. [24]FARKASH,NOSZTICZIUSZ.GeneralizedLotka-Volterraschemesandtheconstructionoftwo-dimensionalexplodatorcoresandtheirLyapunovfunctionsviacriticalHopfbifurcations[J].JChemSocFaradayTrans,1985,81(10):1487-1505. [25]WANGZX,CHENXW,ZHANGWN.Localbifurcationsofcriticalperiodsinageneralized2DLVsystem[J].ApplMathComput,2009,214(1):17-25. [26]HUANGWT,ROMANOVSKIVG,ZHANGWN.Weakcentersandlocalbifurcationsofcriticalperiodsatinfinityforaclassofrationalsystems[J].ActaMathApplSinica,2013,29(2):377-390. [27]CIMAA,GASULLA,SILVAPR.Onthenumberofcriticalperiodsforplanarpolynomialsystems[J].NonlinearAnal,2008,69(7):1889-1903. [28]GASULLA,YUJS.Onthecriticalperiodsofperturbedisochronouscenters[J].JDiffEqns,2008,244(3):696-715. [29]GASULLA,ZHAOYL.Bifurcationofcriticalperiodsfromtherigidquadraticisochronousvectorfield[J].BullSciMath,2008,132(4):292-312. [30]CHENXW,ROMANOVSKIVG,ZHANGWN.Criticalperiodsofperturbationsofreversiblerigidlyisochronouscenters[J].JDiffEqns,2011,251(6):1505-1525. [31]ZHOUJ,LIN,HANMA.Criticalperiodsofperturbationsofreversiblerigidlyisochronouscenters[J].AbstrApplAnal,2013,2013:481501. [32]LIUC,HANMA.Bifurcationofcriticalperiodsfromthereversiblerigidlyisochronouscenters[J].NonlinearAnal:TMA,2014,95(1):388-403. [33]PENGLP,FENGZS.Bifurcationofcriticalperiodsfromaquarticisochronouscenter[J].IntJBifurcChaos,2014,24(6):1450089. [34]LIN,HANMA.Criticalperiodbifurcationbyperturbingareversiblerigidlyisochronouscenterwithmultipleparameters[J].IntJBifurcChaos,2015,25(5):1550070. [35]LULHL,PENGLP,FENGZS.Numberofcriticalperiodsforperturbedrigidlyisochronouscenters[J].IntJBifurcChaos,2016,26(13):1650220. [36]PENGLP,LULHL,FENGZS.Perturbedrigidlyisochronouscentersandtheircriticalperiods[J].JMathAnalAppl,2017,453(1):366-382.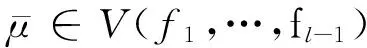
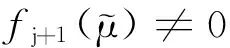
2 二次系统
3 三次系统
4 Liénard系统
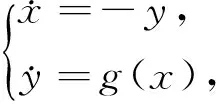

5 非多项式系统


6 刚性等时中心扰动出临界周期





7 结束语
