带有分段常数变量的捕食者-食饵模型的稳定性和Neimark-Sacker分支
2018-04-28豆中丽
豆中丽, 王 锐
(1. 重庆工商大学 融智学院, 重庆 400055; 2. 重庆大学 数学科学学院, 重庆 401331)
种群生态学是生态学中应用较为广泛、发展较为成熟的一个分支,捕食者-食饵系统主要描述生态学中种群之间的相互关系.在生态系统中,具有分段常数变量的微分方程模型的稳定性、分支、混沌行为越来越受到学者们的关注.文献[1]讨论了如下带有分段常数变量的单种群Logistic模型
其中,t,r,K∈(0,+∞),[t]表示参数t的整数部分.文中讨论了模型在正平衡点处的稳定性和分支行为,当参数r等于某特殊值时,该模型在正平衡点附近出现混沌现象.文献[2]研究了具分段常数变量及干扰的反馈控制模型
解的全局存在性、正平衡点的唯一性、全局渐近稳定性、分支的存在性及其方向和稳定性.文献[3]描述了害虫受天敌、气象环境和植被等外界环境因素的影响,讨论了模型
的正平衡态的稳定性、翻转分支和Neimark-Sacker分支周期解的充分条件以及数值模拟验证理论分析的正确性.文献[4]研究了捕食者对食饵的捕获具有滞后效应的模型
的正平衡态稳定性分析、Neimark-Sacker分支的存在性及其分支方向与稳定性.在上述文献的基础上,本文考虑了具有Holling-III功能反应函数
的捕食者-食饵模型
其中,X为食饵种群密度,Y为捕食者种群密度,r∈(0,1)为食饵内禀增长率,K>0为环境容纳量可解释为食饵所取作物状况,a为捕食者的捕食率,β∈[0,1)为食饵逃避率,捕食种群能捕捉到食饵数量为(1-β)X(t),c∈(0,1]为捕食者捕食食饵的转化率,d为捕食者的死亡率.
根据生态学意义可知,模型(1)的初始条件为
X(0)=X0>0,Y(0)=Y0>0.
1 平衡点的存在性和稳定性
下面讨论模型(1)解的存在性、正平衡点唯一性及给出模型在平衡点处的稳定性分析.
定理1.1模型(1)满足初始条件的解在t≥0存在且有界.
证明可利用反证法与比较原理进行证明.

证明模型(1)的平衡点满足方程
令
因为f(Y)是R+上的连续函数,且
f(+∞)=-∞.
当n≤t≤n+1(n=0,1,2,…)时,系统(1)转化为
(2)
对(2)式两端从n到t积分,令t→n+1,化简得到
(3)
通过计算求得:对于任何参数,系统有不动点E0(0,0)、E1(K,0);当ac-d>0,K>K0时,系统(3)存在唯一正平衡点
其中
定理1.3模型(3)的平衡点E0(0,0)是鞍点.
证明模型(3)的Jacob矩阵为
其中

当(X(n),Y(n))=(0,0)时,由模型(3)可知对应的线性系统[5]的特征方程
(λ-er)(λ-e-d)=0,
则
λ1=er,λ2=e-d.
因为r>0,由此可知|λ1|>1,|λ2|<1,所以平衡点E0(0,0)是鞍点.
定理1.41) 当0 (i) 当K(1-β)(ac-d) (ii) 当K(1-β)(ac-d)>d时,平衡点E1(K,0)是鞍点. 2) 当r>2,K(1-β)(ac-d)>d时,平衡点E1(K,0)是不稳定的. 3) 当r≠1,r≠3且K(ac-d)(1-β)=d时,模型在平衡点E1(K,0)处产生flip分支. 证明模型(3)在平衡点E1(K,0)的Jacob矩阵 其中 1) 当0 (i) 当K(1-β)(ac-d) (ii) 当K(1-β)(ac-d)>d时,|λ1|<1,|λ2|>1,所以E1(K,0)是鞍点. 2) 当r>2,K(1-β)(ac-d)>d时,|λ1|>1,|λ2|>1,所以E1(K,0)是不稳定的. 3) 当r≠1,r≠3且K(ac-d)(1-β)=d时,|λ1|≠1且|λ2|=1,所以模型在E1(K,0)处产生flip分支. 4) 当 且 5) 当 d(1+ac-d)K=(ac+(1+ac-d)d)K0 其中 模型的正平衡点的稳定性由特征方程的特征根所决定,令 p(λ)=λ2+μ1λ+μ2, 可求解得到 由此可得特征根 通过计算可知,当ac-d>0,K>K0时, 1) 由 d(1+ac-d)K-(ac+(1+ac-d)d)K0<0, 可得 令 2) 当 3) 当 d(1+ac-d)K-(ac+(1+ac-d)d)K0>0, 4) 当 5) 当 2分支解的存在性和稳定性 处的Jacob矩阵 可得特征根 其中 设p、q分别是对应于特征值eiθ0、e-iθ0的特征向量: Aq=eiθ0q,ATp=e-iθ0p. 为了必要的标准化 可取 通过计算此系统可表示为 这里O(‖x‖4)是高阶无穷小量,B(x,y)和C(x,y,z)是多重线性函数,且在坐标下的分量为: 于是 具有Neimark-Sacker分支的系统出现闭不变曲线的方向,可用下面的公式计算: 下面通过实例,运用Matlab软件绘出相应的分支图[9],并通过图形说明该模型复杂的动力学行为.当参数r=r0=0.68时,产生Neimark-Sacker分支,如图1;当r>r0=0.68时,在正平衡点处失稳经过反复迭代系统出现混沌现象,如图2.使用数值模拟验证参数对模型稳定性和分支周期解的存在性影响,当分支参数的临界值发生变化,系统也在发生变化,可见系统对初值的敏感性,初值经过反复迭代,系统失稳出现分支情形,最后产生混沌现象. 图 1 Neimark-Sacker分支解相平面图 本文讨论了带有分段常数变量的捕食者-食饵模型并通过计算得到模型对应的差分方程. 首先,讨论了模型在正平衡点处的情形,模型在平衡点处是鞍点. 2) 当r>2,K(1-β)(ac-d)>d时,平衡点E1(K,0)是不稳定的. 3) 当r≠1,r≠3且K(ac-d)(1-β)=d时,模型在平衡点E1(K,0)处产生flip分支. 其次,讨论了模型的内禀增长率 最后,使用数值模拟的方法当r=r0=0.68时,产生Neimark-Sacker分支;当r>r0=0.68时,在正平衡点处失稳.初值经过反复迭代趋于∞时,系统的分支会越来越多越来越密,最后进入混沌状态,从而验证了理论结果的正确性. [1] 马知恩. 传染病动力学的数学建模与研究[M]. 北京:科学出版社,2004 [2] 陈斯养,靳宝. 具分段常数变量及干扰的反馈控制模型的N-S分支[J]. 工程数学学报,2015,32(1):85-97. [3] 王烈. 带有分段常数变量和避难所的天敌-害虫模型的稳定性和分支行为[J]. 高校应用数学学报,2014,29(4):431-442. [4] 陈斯养,靳宝. 一类具分段常数变量的捕食-食饵系统的Neimark-Sacker分支[J]. 生态学报,2015,35(7):2339-2348. [5] LIU P, GOPALSAMY K. Global stability and chaos in a population model with piecewise constant arguments[J]. Appl Math Comput,1999,101(1):63-88. [6] ELAYDI S, GEHRING F W, RIBET K A. An Introduction to Difference Equations[M]. New York:Springer-Verlag,2005. [7] 陈斯养,张艳. 具有分段常数变量的捕食-被捕食模型的分支分析[J]. 兰州大学学报(自然科学版),2012,48(3):103-112,117. [8] KUZNETSOV YURI A. Elements of Applied Bifurcation Theory[M]. New York:Spinger-Verlag,2004. [9] 王烈,陈斯养. 带有分段常数变量的Lorenz系统的稳定性和分支[J]. 应用数学,2014,27(4):805-811. [10] 徐昌进. 具有时滞和Holling III型功能反应函数的离散捕食模型的周期解[J]. 四川师范大学学报(自然科学版),2013,36(5):686-690. [11] 马超,黎定仕. 一类非自治微分积分方程的全局指数稳定性[J]. 四川师范大学学报(自然科学版),2014,37(5):639-642. [12] 李亚男,冯广庆,王玉光. 一类考虑存活率的时滞SIR传染病模型的Hopf分支研究[J]. 四川师范大学学报(自然科学版),2016,39(5):649-654. [13] 杜燕飞,肖鹏,曹慧. 具有阶段结构的周期SEIR传染病模型的动力学性态[J]. 四川师范大学学报(自然科学版),2017,40(1):73-77.




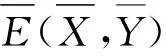











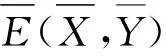



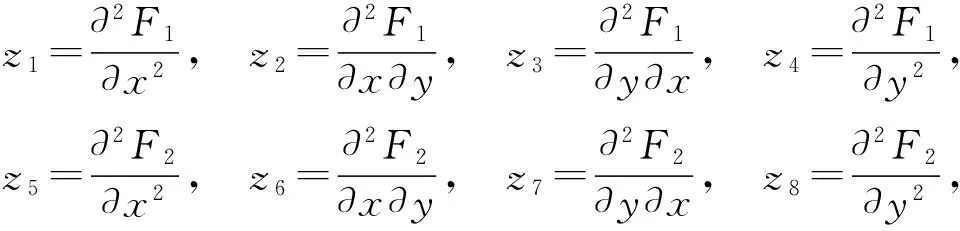








3 总结和讨论
