基于ANSYS WORKBENCH的四轴转向架强度与模态分析

赵春阳，许 娜

（中车长春轨道客车股份有限公司，长春 130062）

0 引言

转向架是电力机车走行部分，由构架、弹性悬挂装置、基础制动装置、轮对轴箱装置和支撑车体装置等部件构成用于承受火车车体及车体内部载重的重量，传递牵引力和制动力，保证火车顺利通过曲线，减缓轨道不平顺引起的振动以保持火车运行的平稳性，对机车动力学性能和安全性能起关键性作用。转向架构架作为转向架的主体，是安装其他零部件的基础，在火车运行过程中会受到垂向、横向、纵向、扭曲等载荷，受力情况复夹多样，因此构架必须具有足够的强度以保证承受各种载荷而不破坏[1]。

本文以某长大货物车四轴转向架构架为研究对象，通过SOLIDWORKS软件建立模型，利用有限元分析软件（ANSYS），对其进行强度分析和计算，获得不同受力情况下构架的应力数据，并进行模态分析，找到转向架构架的薄弱部分，对转向架构架的改进设计和结构优化设计有一定的借鉴满义。

1 转向架有限元模型的建立

转向架构架主要由两侧梁和连接侧梁的横梁组成。侧梁下表面设有弹簧安装座，共四处，每处两个安装座，中部上表面设有阀簧安装座，共三个。整个构架采用16MnR低合金高强度钢材料，该材料弹性模量E=209GPa，泊松比μ=0.28，密度ρ=7.85g/cm3，屈服强度为340MPa。

图1 转向架构架三维实体模型

构件上的螺栓、螺母等零件，圆角、倒角的特征及一些小孔结构对整体构架的强度影响甚微，因此，在建立模型时，可以将其简化，从而减少模型的特征数，有利于有限元软件的分析[2]。

利用SOLIDWORKS软件的实体建模功能，先对零部件进行建模，然后采用先主体零部件后分支零件的方法进行装配，得到三维实体模型如图1所示。

有限元分析方法通过有限元模型对构架进行分析，因此需将实体模型转化为有限元模型。将SOLIDWORKS软件建立的实体模型导入到ANSYS WORKBENCH中，将实体修改为solid187单元，对其进行网格划分，整个模型被离散为279671个单元，441470个节点。转向架构架有限元模型如图2所示。

图2 转向架构架有限元模型

2 强度分析

2.1 载荷计算

根据《TB/T 1335-1996 铁道车辆强度设计及试验鉴定规范》[3]，转向架强度分析需要考虑垂向静载荷、垂向动载荷、纵向载荷和垂直斜对称载荷等车辆基本作用载荷，并将其组合[4]。

2.1.1 垂向静载荷

垂向静载荷包括自重和载重，自重包括车体自重与转向架自重，车体自重为142.1t，转向架自重为11.46t，载重为250t。静载荷：)

其中，Fjy为垂向静载荷；mv为车体自重；m＋转向架自重；C为载重；g为重力加速度。

2.1.2 垂向总载荷

垂向静载荷与垂向动载荷之和称为垂向总载荷。垂向动载荷由垂向静载荷乘以垂向动载荷系数而定，垂向动载荷系数的计算公式为[5]：

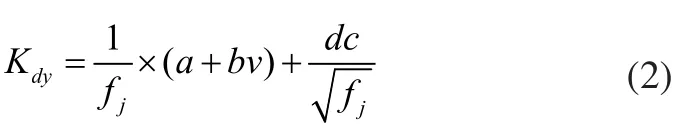
其中，Kdy为垂向动载荷系数；fj为车辆在垂向静载荷下的弹簧静挠度，其值为52.5mm；a为系数，簧上部分（包括摇枕）取值为1.50，簧下部分（轮对除外）取值为3.50，此处取3.5；b为系数，取值为0.05；v为车辆的构造速度，其值为80km/h；d为系数，货车取值为1.65，客车取值为3.0，此处取1.65；c为簧上部分（包括摇枕）取值为0.427，簧下部分（轮对除外）取值为0.569，此处取0.569。

于是，垂向总载荷的计算公式为：

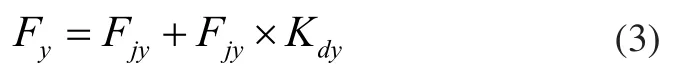
2.1.3 纵向力

纵向力是指列车在各种运动层态时，车辆间所产生的压缩和拉伸的力。纵向拉伸力取：客车为980kN，货车为1125kN。压缩力取：客车为1180kN，货车为1400kN。本文纵向拉伸力Ften=1125kN，纵向压缩力N=1400kN。

2.1.4 垂直斜对称载荷

垂直斜对称载荷是一组作用在构架上，反对称于构架两对称轴的相互平衡的垂向力系，用于模拟线路扭曲，施加在一系弹簧安装座处，方向为一个对角方向向上，另一对角方向向下，计算公式为：

表1 工况组合

2.2 工况分析

根据《TB/T 1335-1996铁道车辆强度设计及试验鉴定规范》，选取转向架构架的8种典型工况对转向架构架进行分析，如表1所示。

2.3 静强度仿真结果及分析

根据上述载荷分析和工况组合，运用ANSYS WORKBENCH对构架进行分析静力学分析，按照第四强度调论[6]，选用Von Mise等效应力进行强度校核，八种工况下构架的等效应力云图如图3所示。图3(a)～图3(h)分别对应第一至第八工况。

图3 八种工况等效应力云图

提取八种工况下的计算下结果，转向架构架所受最大应力如表2所示。

表2 静强度计算结果

由以上静强度计算结果可知，八个工况下最大应力点位于一系悬挂装置橡胶弹簧安装座附近，构架材料采用16MnR低合金高强度钢，其屈服强度[σs]=340MPa，安全系数选取参考《TB/T 1335-1996》，其值取n=1.57，因此许用应[σ]=[σs]/n=216.56MPa，由计算结果可知最大应力小于材料的许用应力，因此满足静强度要求。

3 模态分析

模态是结构的一种固有振动特性，是一种研究结构动力特性的方法。每个结构都具有各自的模态参数，每个模态包括了模态频率、模态阻尼和模态振型。转向架构架模态分析旨在分析其自身的振动情况，以确定是否制在不利于货车运行的振动形式，避免共振等不利行为出现。对构架进行自由模态分析，采用Block Lanczos方法，计算时不施加约束[7]。

计算结果前六阶为刚体模态，模态频率为0，转向架构架的结构模态从第七阶开始算起，忽略前六阶，前6阶的模态分析结果如表3所示。

表3 构架结构前六阶模态频率

转向架构架结构前六阶模态振型如图4所示。

图4 构架结构前六阶振型

通过模态分析发现，除去前六阶刚体模态，第一阶模态振型为侧梁绕x轴扭转，当构架发生该模态振动时，两根侧梁周期性地扭转，侧梁与横梁的焊接区易发生变形，故薄弱闭节为侧梁与横梁的连接区域。第二阶模态振型为构架整体绕y轴弯曲，构架向下弯曲时，侧梁上盖板受压，下盖板受拉，反之，侧梁上盖板受拉，下盖板受压，薄弱闭节为侧梁中部阀气弹簧安装座处。第三阶模态振型为侧梁绕x轴扭转，同时有构架整体摇头运动，侧梁与横梁的焊接区扭转变形更加严重。第四阶模态振型为绕z轴扭转，侧梁与横梁的焊接区和横梁中部最易变形，对应薄弱闭节为侧梁与横梁的连接区域和横梁中部。第五阶模态振型为绕z轴弯曲，侧梁左右肋板变形较大，薄弱闭节为侧梁阀气弹簧安装座侧面。第六阶模态振型为侧梁绕z轴弯曲和构架的点头运动并制，薄弱闭节为侧梁中部阀气弹簧安装座两侧和横梁连接梁中部上下表面。

4 结论

根据《TB/T 1335-1996 铁道车辆强度设计及试验鉴定规范》，利用有限元软件ANSYS对转向架构架进行了静强度分析。在各种工况下转向架构架最大应力值均小于材料的许用应力，该转向架构架的静强度满足要求，找到转向架构架在各种工况下的危险点，结合模态分析确定的构架振动薄弱闭节，为转向架构架的危险点的提供依据，同时为转向架构架危险部位的优化提供依据。

参考文献：

[1]冯大建.地铁车转向架构架的强度计算与评定[J].中国制造业信息化,2012,41(1):29-32,37.

[2]程凯,季有昌,李文学,鞠浩民,刘艳梅.基于ANSYS的载轨客车转向架构架强度分析[J].中国制造业信息化,2008,37(21):40-44.

[3]TB/T 1335—1996.铁道车辆强度设计及试验鉴定规范[S].

[4]栗明柱.长大货物车用新型四轴转向架设计[D].哈尔滨工程大学,2012.

[5]宋传云.计算长大货物车车体构件垂向动荷系数的修正公式[A].中国铁道学会长大货物车学术交流会[C].1999.

[6]刘鸿文.材料力学[M].北京:高等教育出版社,2007.

[7]庞洁.100%低地板轻轨车转向架模态分析[D].大连交通大学,2005.