基于模糊逻辑的PMSM转矩谐波反馈控制

帅海燕，邹必昌

(1.武汉交通职业学院，武汉 430065；2.长江大学，荆州 434023)

0 引 言

基于永磁同步电机(以下简称PMSM)的伺服系统存在的转矩脉动将产生机械振动和噪声，这将降低系统性能和应用范围，如电动汽车或机器人系统等[1-2]。故有较多文献开展了对转矩脉动优化控制的研究[3-6]，具体而言，大多数控制策略可分为两类，一种是优化电机设计[3-4]，以降低齿槽转矩或特定次磁链谐波；另一种是施加先进的控制策略[5-6]，控制定子电流以对转矩脉动进行抑制。其中后一类方案具有较好的通用性从而应用广泛。

转矩脉动控制的关键是优化定子电流以补偿对应的转矩谐波[7]，可分为前馈补偿方法和反馈控制方法。前馈补偿方法需要准确的转矩脉动模型来确定最优定子电流。例如，文献[8]中设计了一种基于神经网络的最优定子电流计算方法，但高度依赖于电机参数。由于模型和预测受到磁饱和和其他系统非线性因素影响，难度较大[9]。而反馈控制方法则基于转矩估计实现反馈控制以降低转矩脉动，但需要较高的估计精度。文献[10]提出了一种转矩预测控制来最小化转矩脉动。然而，依然对电机参数变化敏感，即预测转矩没有独立的实际测量，若测量转矩则意味着高昂的成本，是难以工程应用的。此外，文献[11]和文献[12]使用转速误差进行转矩脉动抑制，原理是速度谐波和转矩谐波相关联的。其中文献[12]结合使用了转速误差反馈和迭代学习控制策略用于控制转矩脉动，但并未考虑转速误差包含了一些非转矩脉动引起的谐波，且计算负担重。

本文基于上述研究提出了一种使用转速谐波幅值作为反馈控制信号的新型转矩脉动抑制方案。由于转速谐波可从转速编码器获得，所以避免了一些系统非线性因素的影响。首先，对转矩谐波与转速之间的关系进行了建模。然后，分析定子谐波电流如何对转矩脉动产生影响，为电流控制器的设计奠定基础。最后通过试验对新方案进行了验证。

1 转速谐波和转矩谐波关系分析

PMSM的机械方程[10]：

ωm

(1)

式中：Te为PMSM的输出转矩；TL为负载转矩；J为转动惯量；B为粘性摩擦系数；ωm为转子机械转速。从式(1)可以看出，转矩谐波可以导致相同次的转速谐波。为此，将转矩和转速写成直流分量和谐波分量组合的如下形式：

θ-φek)

(2)

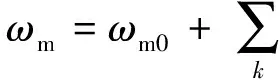
(3)

式中：Te0为平均转矩；Tek和φek为第k次转矩谐波的幅值和相角；ωm0为平均转速；ωmk和φωk为第k次转速谐波的幅值和相角；θ为转子位置。将式(2)和式(3)代入式(1)，同时假设负载转矩不存在谐波，则可得到：

Te0-TL=Bωm0

(4)

Tekcos(kθ-φek)=Bωmkcos(kθ-φωk)-

kJpωm0ωmksin(kθ-φωk)

(5)

式中：p是极对数。基于式(5)，转矩谐波幅值和转速谐波幅值的关系：

考虑到实际中B远小于kJpωm0，所以式(6)可简化：

Tek=kJpωm0ωmk

(7)

从式(7)可看出，第k次转速谐波幅值ωmk正比于第k次转矩谐波幅值Tek，而与平均转速ωm0成反比。ωmk可从转速测量中获取，故考虑作为反馈信息。

根据文献[7]，PMSM的转矩谐波通常由几个数量有限的频次为主导，如6次和12次谐波，根据实际测试，试验用PMSM的转矩谐波以12次谐波为主导，图1为试验测得的第12次转矩谐波幅值和转矩谐波幅值的关系曲线。曲线验证了式(7)的正确性，下面将利用ωm12作为反馈信号进行转矩脉动优化控制。

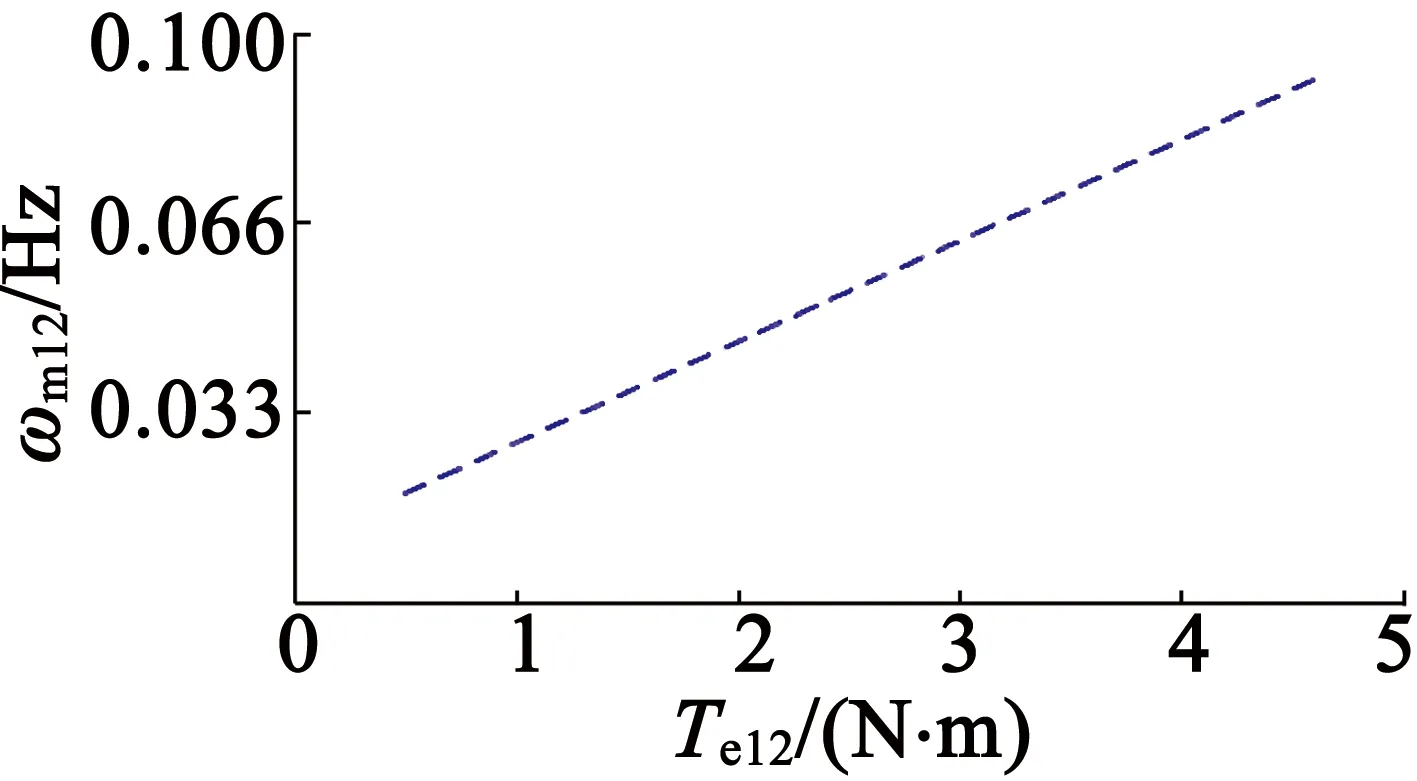
图1第12次转矩谐波幅值和转速谐波幅值的关系曲线

2 转矩脉动建模

由PMSM输出转矩公式[10]：

式中：Ldq=diag{Ld,Lq}为d-q轴电感矩阵;λdq=[λd,λq]T和idq=[id,iq]T分别为d，q轴磁链矢量和电流矢量;Tcog为齿槽转矩;“×”是交叉乘积符号，具体定义：

从式(8)可看出，转矩谐波主要是由磁链谐波、电流谐波和齿槽转矩引起的。当电机设计完成后，磁链谐波和齿槽转矩不可控，但可以通过注入受控电流抑制转矩纹波。

d-q轴磁链表达式和齿槽转矩[13]表达式如下：

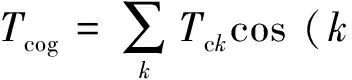
(11)

式中：λ0为磁链直流分量；λdk和λqk为第k次d，q轴磁链谐波分量；φλk为对应相角；Tck是齿槽转矩的第k次谐波分量；φck为对应相角。

图2为试验用电机的额定工况下转矩波形和主要频次的频谱。从图2中明显看出，第12次谐波占谐波含量的主导，故后续采用其作为控制对象，令k=12，如果电机含有多个主导谐波分量则可以分别对其进行建模。将式(10)和式(11)代入式(8)，可得：

(a) 转矩波形

(b) 谐波频谱

图2额定负载条件下的PMSM转矩波形和频谱

Te=Te0+Te12m

(12)

Te0=1.5p[λ0iq0+(Ld-Lq)id0iq0]

(13)

Te12m=βcos(12θ-φ)+Tc12cos(12θ-φc12)

(14)

式中：id0和iq0为d，q轴电流的直流分量。为了抑制转矩谐波，控制定子电流分为两个部分：一部分用于产生所需转矩平衡负载转矩；另一部分为谐波电流用于最小化转矩脉动。具体如下：

式中：idq0=[id0,iq0]T为d，q轴直流电流矢量；idqk是第k次谐波电流；idk和iqk为谐波电流幅值；φik为对应相角。如前所分析，第12次谐波占主导，故考虑k=12后的式(17)简化：

将式(18)代入式(8)中，则由第12次电流谐波产生的第12次转矩谐波：

Te12c=αcos(12θ-φ)

(19)

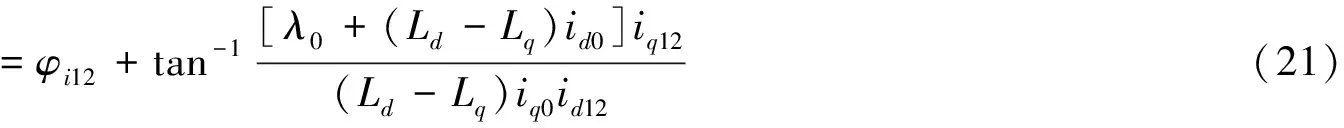
基于式(14)和式(19)，第12次转矩谐波总和：

Te12=Te12m+Te12c=

αcos(12θ-φ)+βcos(12θ-φ)+

Tc12cos(12θ-φc12)

(22)

控制电流idq12可使得Te12c和Te12m相互抵消，以实现转矩脉动抑制。考虑到电流谐波将导致一定的铁损和铜耗，约和谐波幅值的平方成正比[14]。因此，还需要尽量降低谐波幅值。理想情况下，为实现Te12=0控制目标，从而有：

αcos(12θ-φ)+βcos(12θ-φ)+

Tc12cos(12θ-φc12)=0

(23)

简单推导即有：

αcos(12θ-φ)=-βcos(12θ-φ)-

Tc12cos(12θ-φc12)

(24)

仅考虑上式的幅值，结果：

α={(βcosφ+Tc12cosφc12)2+

(βsinφ+Tc12sinφc12)2}12=

基于上式，谐波电流幅值必须满足：

(26)

此外，从式(20)可以看出，对于表贴式PMSM：

1)d轴电流谐波不会产生转矩纹波；

2) 若幅值相同，d轴谐波电流较之q轴谐波电流将产生较少的转矩脉动。故仅考虑注入q轴谐波电流，从而式(20)和式(21)可以简化：

α=1.5p[λ0+(Ld-Lq)id0]iq12

(27)

φ=φi12+π2

(28)

将式(27)代入式(26)可得：

φi12∈[0,2π]

(30)

从式(19)～式(22)可以看出，iq12和φi12对第12次谐波幅值都具有影响，故分析计算了两者不同取值下，第12次转矩谐波幅值的分布如图3所示。图3中iq12从1 A变化至3 A，而φi12从π2变化至3π2。基于图3，给定一个固定的iq12，随着φi12的增加，Te12的幅值先减小，然后再增加。当φi12在[0.7π，1.3π]范围内，对于一个固定的φi12，随着iq12的增加，Te12的幅值也是先减小，然后再增加。下面将基于此进行模糊逻辑控制器(以下简称FCL)的设计。

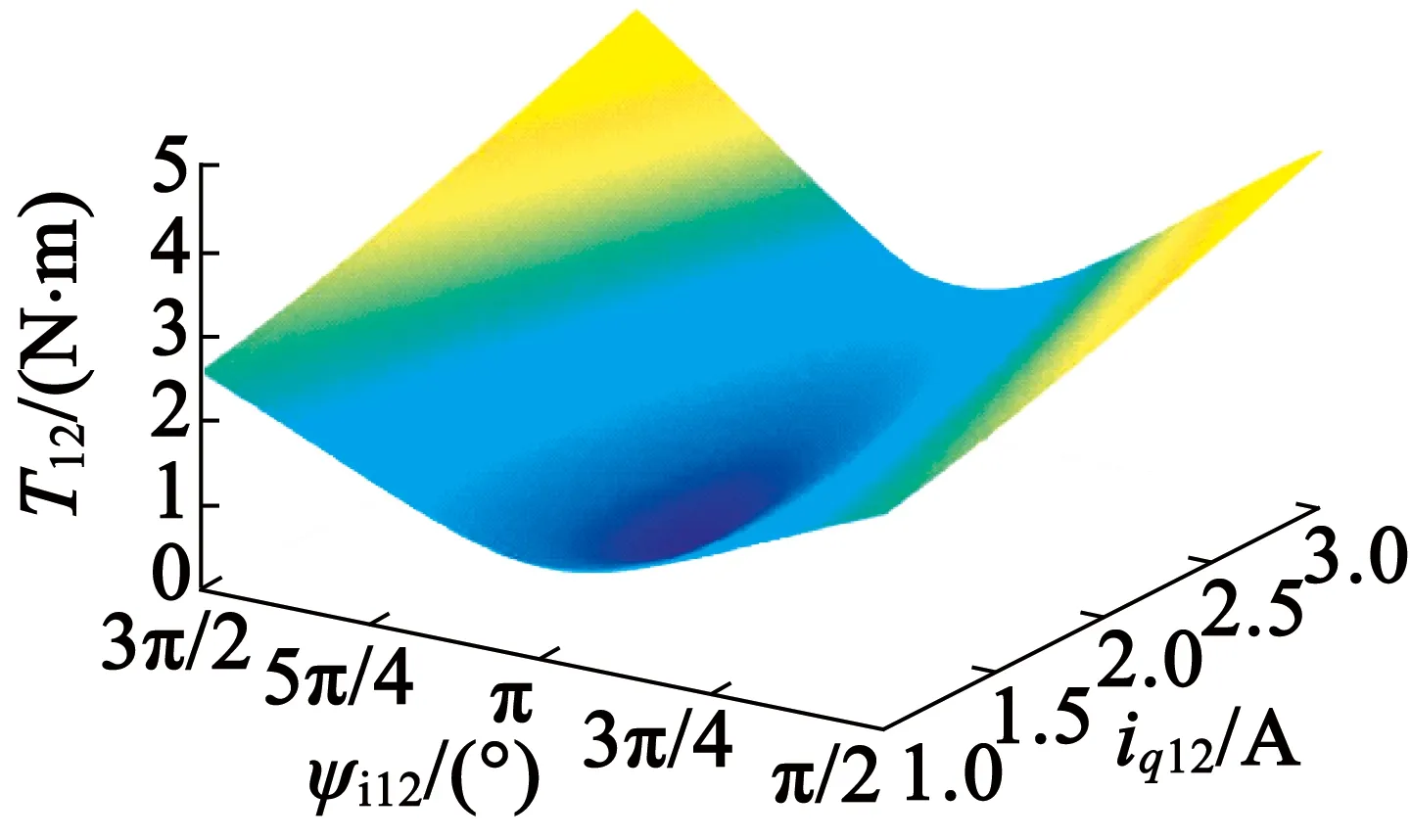
图3第12次电流谐波幅值、相角与第12次转矩谐波的关系

3 基于模糊逻辑的闭环电流控制

设计FLC的主要目标是使用第12次电流转矩谐波幅值作为反馈来抑制转矩脉动Te12，其次尽量减少谐波电流的幅值以减小谐波电流带来的损耗。图4为FLC控制器的框图。FLC的输入参数是转速谐波幅值ωm12及其导数Δωm12，具体如下：

ωm12(t)=H_D[ωm(t)]

(31)

式中：t代表时间；Δt为采样时间。在实际控制器实施中，为了减小计算负担，采用一种新型的速度谐波检测H_D(ωm(t))取代FFT算法来检测速度谐波，具体见后续试验部分。

图4分层模糊逻辑控制器框图

FLC控制器的输出谐波电流的幅值iq12和相角φi12用于最小化Te12，iq12和φi12需要满足式(29)和式(30)。FLC可以被视为输入语言变量ωm12和Δωm12到输出语言变量iq12和φi12的映射，可表示：

u(t+1)=FLC[ωm12(t),Δωm12(t)]

(33)

式中：u包含两个输出iq12和φi12。FLC设计采用分层结构，即iq12和φi12输出解耦，然后两个控制单元FLC1和FLC2交错控制，直至转矩谐波幅值最小化。首先，控制器初始设置较小电流量级并调节相角，直到转速谐波幅度最小化。如果转速谐波大小在可接受水平内，即进行保持；否则，控制器就将增加电流幅值，再次调节相角以期达到更好效果。持续上述步骤直至转速谐波到可接受水平。

如图4所示，FLC的两个单元FLC1和FLC2具体：

从式(34)更明显地看出，FLC1控制φi12，FLC2控制iq12。每个FLC单元都由3个部分组成，模糊化模块、模糊推理模块和去模糊化模块。即模糊化模块用于将输入变量ωm12和Δωm12转化为相应的语言变量，模糊推理模块的任务是根据输入语言变量获取控制规则，去模糊化模块将控制规则转换为输出控制量iq12和φi12。图5为标幺后ωm12和Δωm12的隶属函数，其中ωm12分解为两个模糊区，即零和正，而Δωm12转化分解为3个模糊区，即零、正和负。具体的模糊分区阈值如图5所示。

(a)ωm12的隶属函数

(b) Δωm12的隶属函数

图5隶属函数示意图

控制器采用了Takagi-Sugeno型模糊推理用于电流控制。具体来说，FLC1单元的目标是在时间t内通过适当调节相角φi12减小ωm12，从而FLC1的模糊控制规则如下：

1) 如果ωm12为零，则保持φi12。

2) 如果Δωm12为零，则保持φi12。

3) 如果ωm12为正，Δωm12为正，则增加φi12。

4) 如果ωm12为正，Δωm12为负，则减小φi12。

FLC2单元的目标是在时间t内通过适当调节电流iq12减小ωm12，从而FLC2的模糊控制规则如下：

5) 如果ωm12为零，则保持iq12。

6) 如果ωm12为正，Δωm12为零，则增加iq12。

7) 如果ωm12为正，并且Δωm12不为零，则保持iq12。

应该注意的是，在初始阶段，iq12设置为较小的正值，例如最大值的5%。从规则5)至规则7)可看出，iq12更新事件的发生只有在时间t-1内已获取φi12(t-1)。因此，层次化FLC控制器的思路是首先初始化iq12，然后找到最优的φi12。如果ωm12最小化，则停止，否则增加iq12并找到最佳的φi12。故iq12和φi12将迭代更新，直到找到各自最优值。其中iq12每次的增加步长不宜过大，以保证能搜索到最佳值。

去模糊化模块将计算输出最终的iq12和φi12。具体如下：

式中：Kφ和Ki为控制增益参数，具体由以下去模糊化规则决定：

8) 增加φi12，则设置Kφ>0。

9) 保持φi12，则设置Kφ=0。

10) 减小φi12，则设置Kφ<0。

11) 增加iq12，设置Ki>0。

12) 保持iq12，设置Ki=0。

通常控制增益Kφ和Ki的绝对值应该较小，以确保控制器收敛到最佳值。但对于控制增益参数Kφ和Ki，没有一般的方法来选择，通常经过实际试验进行确定，具体见下一节。由于iq12和φi12需符合式(29)和式(30)的范围，故增加下面两条规则：

13) 如果φi12>2π，则φi12=φi12-2π。

14) 保持iq12>iq12max，则iq12=iq12max。

其中iq12max是式(29)限制的最大幅值。此外，转矩谐波的大小取决于定子电流，定子电流发生变化则谐波电流应重新初始化。

4 试验验证

为了验证控制策略，搭建试验平台如图6所示。平台包含测试用PMSM、负载电机、RT-Lab实时控制系统、变频器和各类传感器等,其中PMSM参数如表1所示。图7为空载时的PMSM转矩波形和频谱，而额定负载时的转矩波形和频谱如图2所示。考虑到需要使用转速谐波反馈，故使用了高精度高分辨率的光学编码器用于转速测量。试验中采样频率为50 kHz，开关频率为5 kHz。

图6测试平台

表1永磁同步电机参数

参数数值参数数值额定电流i/A15额定转速n/(r·min-1)575额定转矩T/(N·m)70额定电压u/V275永磁磁链ψ/Wb0．67d轴电感Ld/mH30．4q轴电感Lq/mH87．5极对数p4槽数48

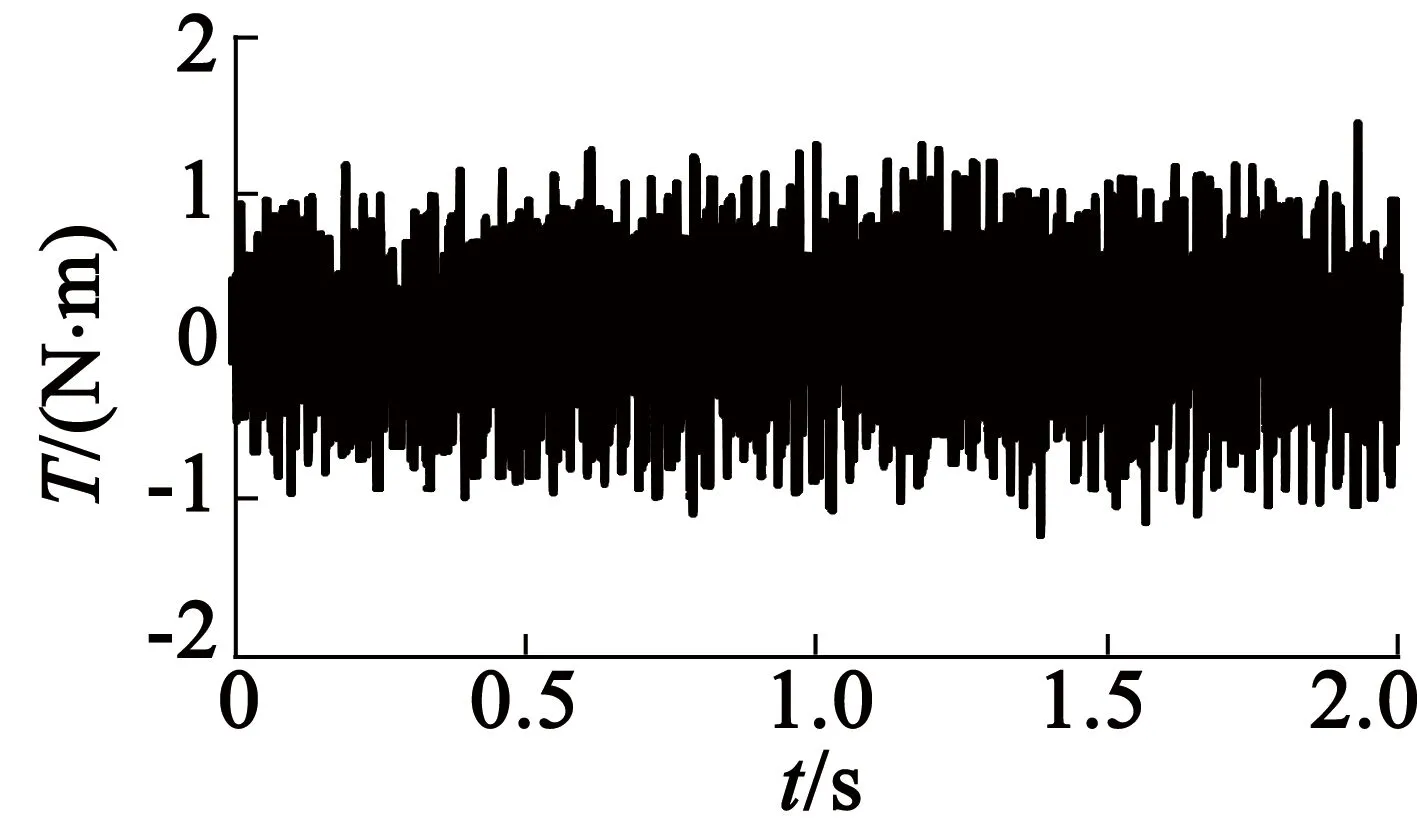
(a) 转矩波形

(b) 谐波频谱

图7空载时的PMSM转矩波形和频谱

首先，对电机反电动势进行测试，并根据式(29)获得谐波电流上限。设abc三相磁链：

式中：λa，λb和λc为a，b，c轴的磁链;而λabc,k为磁链幅值，k=1,3,5,7,…,k为谐波次数。对式(36)进行旋转坐标变换，可得d-q轴磁链：

式(37)中，λ0=λabc,1为直流分量；k=6,12,…，k为谐波次数。如图8(a)为基于FLC的PMSM控制框图。电流的直流分量控制采用了PI控制单元，谐波电流控制采用了PR控制单元，两个控制单元输出进行了叠加形成最终控制输出。图8(b)为第12次转速谐波检测和提取模块。

(a) 控制整体框图

(b) 转速谐波检测和提取模块

图8基于FLC的PMSM控制框图

(1) 试验1

在试验1中，负载转矩大约为35N·m，d，q轴参考电流分别为0和10A，电机转速为100r/min，Kφ和Ki设置为0.001。试验1的目的是为了分析φi12升级规则，图9(a)至图9(d)分别为FLC的两个输入语言变量，ωm12和Δωm12，以及两个控制输出iq12和φi12。从图9中可看出，36s后FLC输出收敛到最佳幅值和相角1.5A和196°。

(a) ωm12

(b)Δωm12

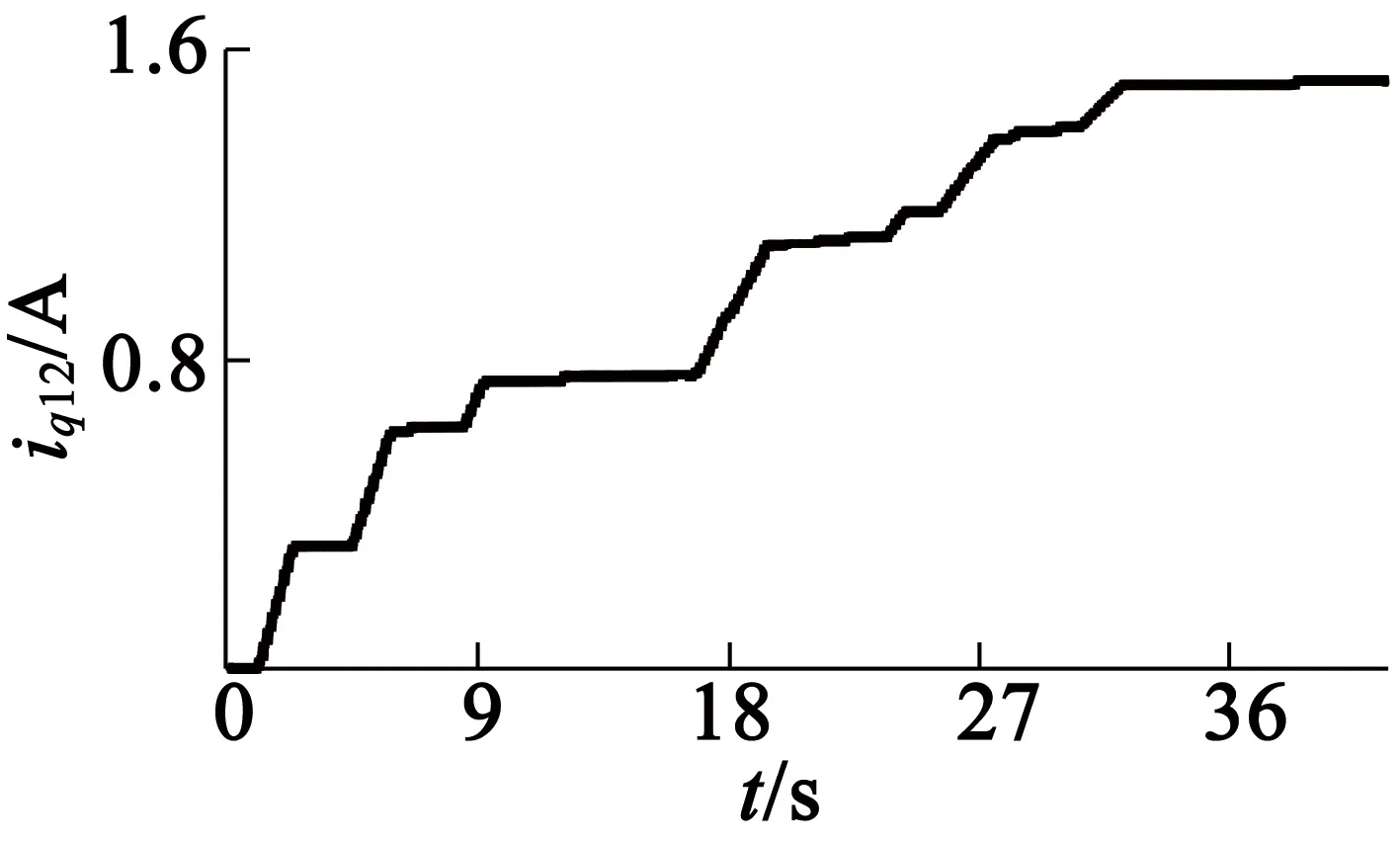
(c) iq12

(d) φi12

图9未考虑φi12升级规则时试验1的FLC输入输出波形

图10(a)至图10(c)分别为q轴电流波形和转矩波形和第12次转矩谐波波形。从图10(a)中可看出，在FLC控制器作用下，q轴谐波电流逐渐增加，直至找到最佳控制点。从图10(b)可看出，转矩脉动得到有效抑制，进一步如图10(c)所示，第12次转矩谐波幅值从4N·m降至0.35N·m。然后从图10中还可看出，控制器收敛过程中存在振荡过程，这是需要避免的，这是在搜索φi12时发生的，即φi12升级规则需要进一步设计。

(a) q轴电流波形

(b) 转矩波形(c) 第12次转矩谐波波形

图10未考虑φi12升级规则时试验1的试验波形

为了消除这种收敛过程中的振荡，需要设计相角的搜索规则，具体如下：

15)如果iq12>ε，则将φi12设为上一步的最佳值，并忽略其他规则对φi12的调节。

其中ε为给定阈值，通过试验测试设置为最大谐波电流的40%。设计好φi12升级规则后的FLC输入输出波形和试验电流、转矩波形分别如图11和图12所示。对比之前的图9和图10可看出，在消除了收敛振荡的基础上，控制性能保持了不变，转矩脉动得到了有效抑制。

(a) ωm12

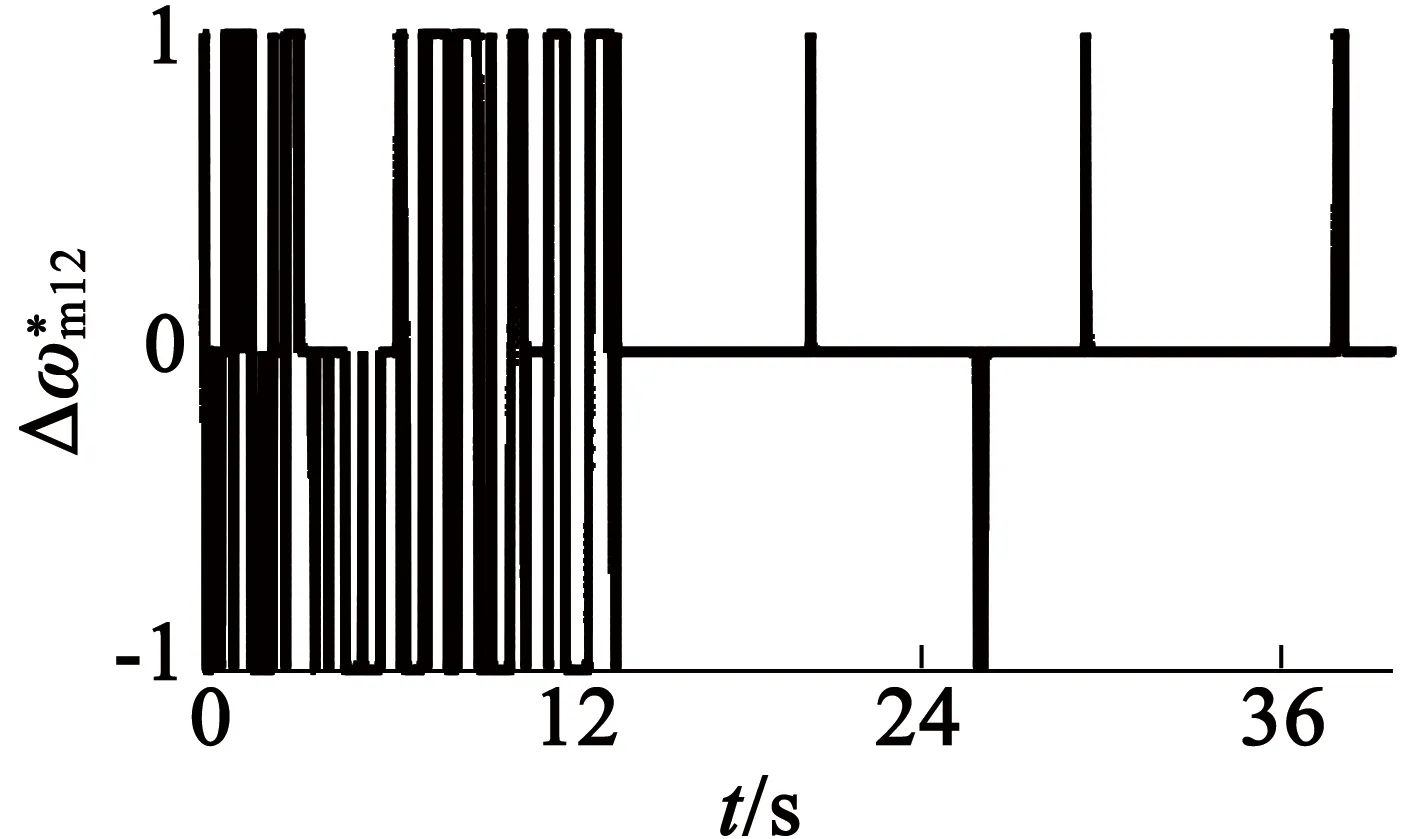
(b)Δωm12

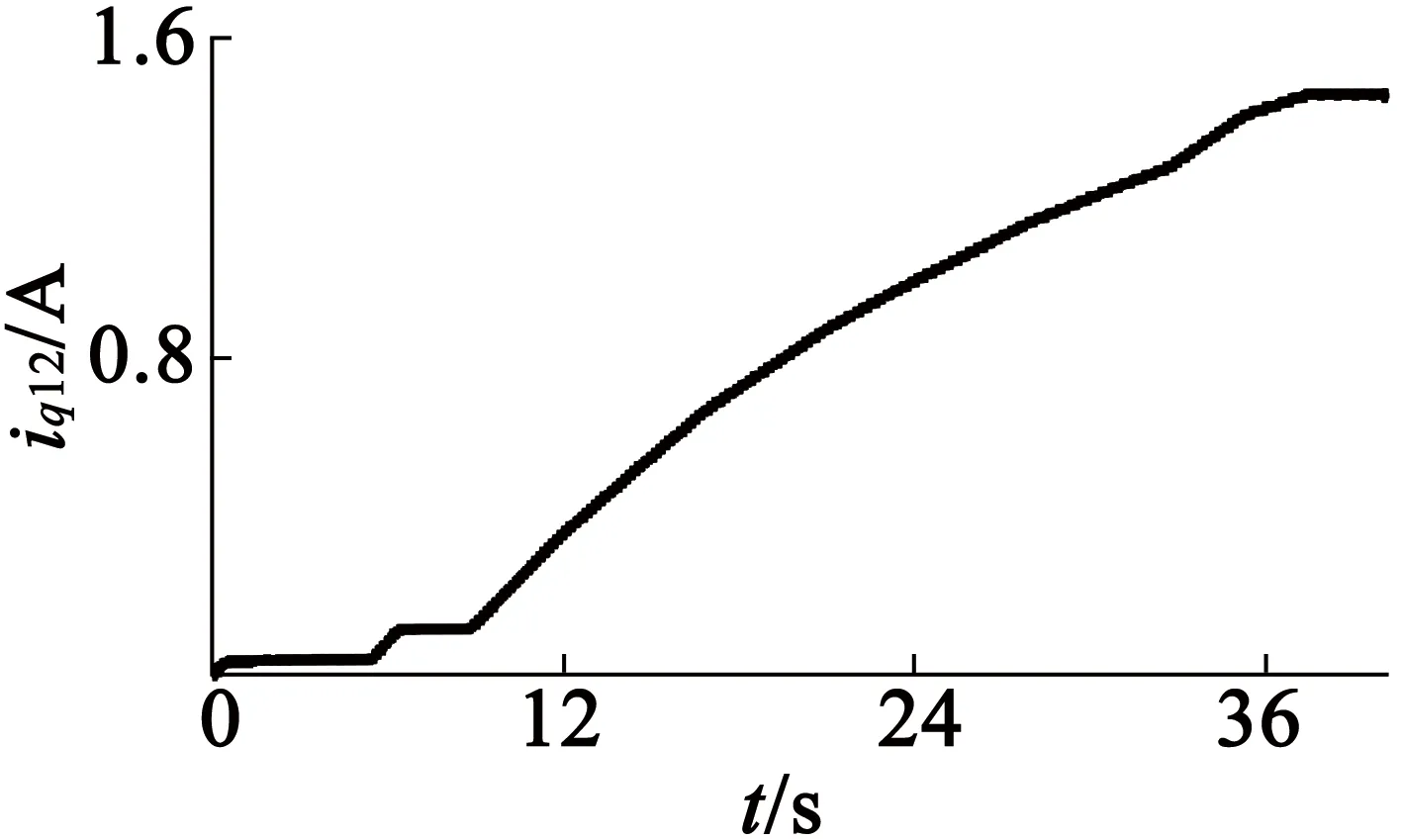
(c) iq12

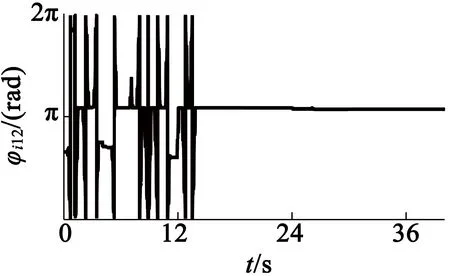
(d) φi12

图11增加φi12升级规则时试验1的FLC输入输出波形

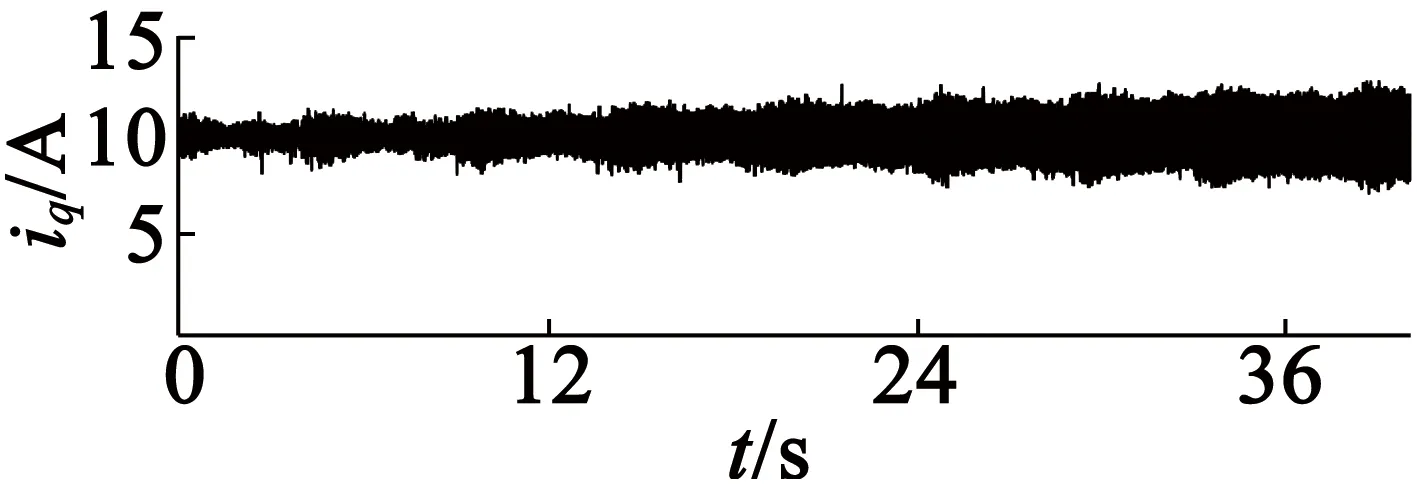
(a) q轴电流波形

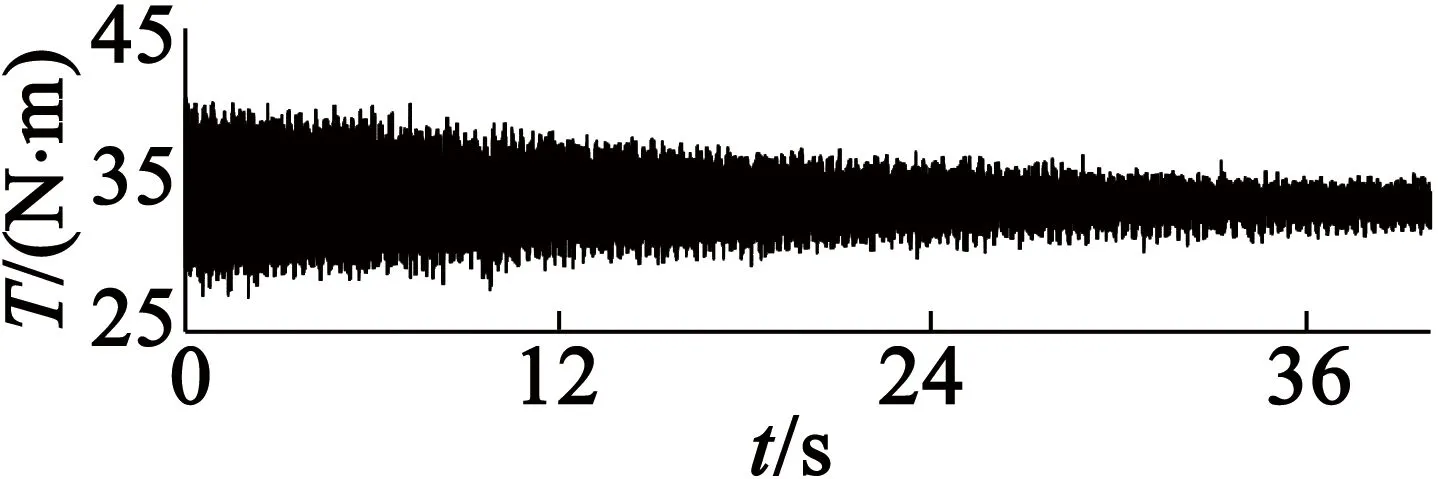
(b) 转矩波形(c) 第12次转矩谐波波形

图12增加φi12升级规则时试验1的试验波形

(2) 试验2

试验2中设置的工况和试验1一致，但设置3组Kφ和Ki：Kφ=Ki=0.01；Kφ=Ki=0.005；Kφ=Ki=0.001，从而分析两者如何影响控制器收敛速度。图13为3组参数下转矩试验波形。从图13中可以看出，随着Kφ和Ki的增大，FLC的收敛速度加快，但同时还需谨慎选择，以避免谐波电流增加太快，导致动态性能降低。

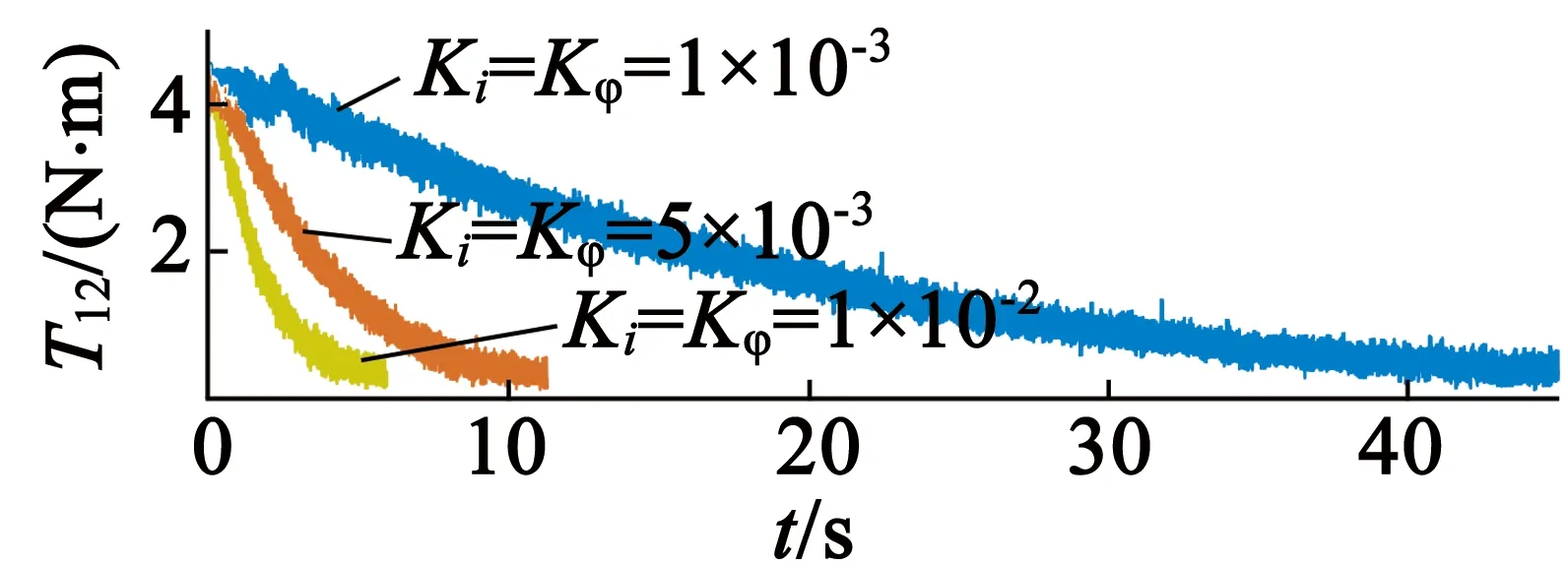
图13参数变化时的转矩试验波形

(3) 试验3

试验3中电机转速设定为100r/min，然后设置Kφ=Ki=0.01，进行了较大负载70N·m工况和较小负载20N·m工况下的测试，图14为转矩试验波形。从图14(a)中可以看出，负载为70N·m时，转矩脉动在FLC控制器作用下明显减小，收敛大约需要12s。而从图14(b)中可看出，当负载为20N·m时，转矩脉动在约6s后即收敛到最小值。试验结果验证了控制策略在不同负载工况下效果都较好。

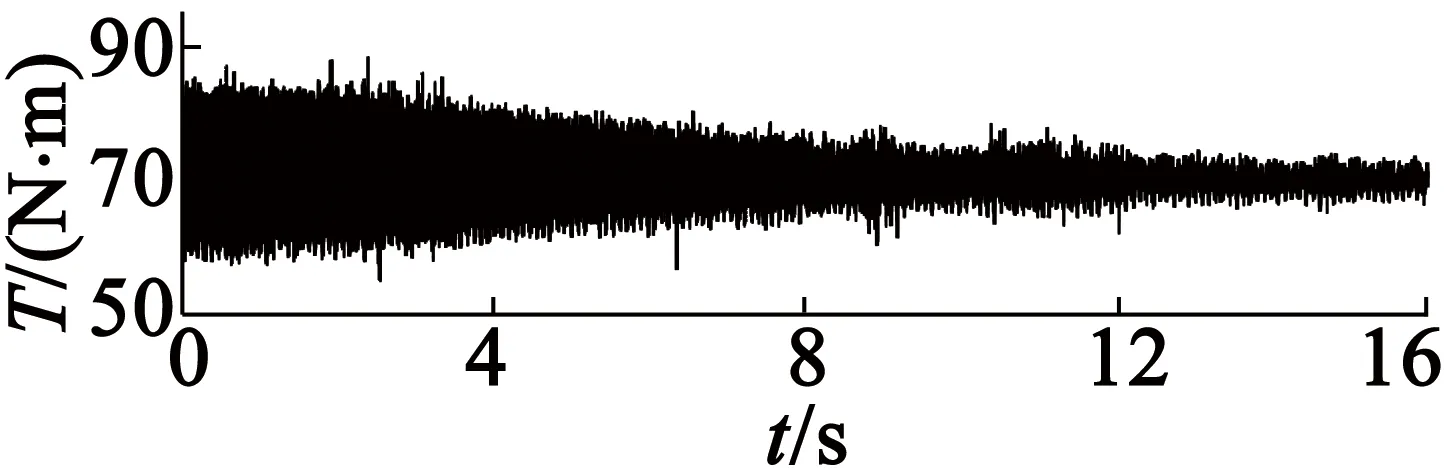
(a) 负载转矩70N·m

(b) 负载转矩20N·m

图14不同负载下的转矩试验波形

5 结 语

围绕PMSM转矩脉动问题，本文设计了一种基于FLC和转速谐波反馈的转矩脉动优化控制，通过分析设计和试验，现总结主要结论如下：

1)通过对转矩脉动建模，转矩谐波和转速谐波存在内在联系，并可通过谐波电流进行抑制。

2)试验结果表明，通过引入转速谐波反馈，并基于FLC设计闭环控制器，可有效降低转矩脉动。

3)新型控制策略针对的是主导转矩谐波抑制，可推广到不同型号PMSM，只需提前对转矩脉动进行测量分析即可。

4)FLC闭环具有计算简单易于实现的优点，但是也存在动态性能慢的不足，进一步研究方向可以分析如何提高转速暂态下的转矩谐波抑制。

[1] 戴彦．基于电动汽车的永磁同步电动机模糊自抗扰控制研究[J]．微特电机，2015，43(7)：85-88．

[2] 徐殿国，王宗培．机器人直接驱动系统的发展现状与展望[J]. 电工技术学报，1988，(3)：55-60．

[3] 方程，许海平，薛劭申，等．直驱型多相永磁同步电机转矩脉动及损耗特性[J]. 电工技术学报，2014，29(5)：149-159．

[4] 王艾萌，温云．基于混合遗传算法的内置式永磁同步电机的优化设计[J]．电机与控制应用，2017，44(3)：59-65．

[5] 齐美星，童敏明．永磁同步电机转矩脉动占空比最优控制方法[J]．电气传动，2015，45(1)：14-18．

[6] 荣智林，陈启军．具有死区补偿的自抗扰控制下PMSM转矩脉动抑制方法[J]．控制与决策，2016，31(4)：667-672．

[7] 廖勇，甄帅，刘刃，等．用谐波注入抑制永磁同步电机转矩脉动[J]．中国电机工程学报，2011，31(21)：119-127．

[8] 赵君，刘卫国，骆光照，等．永磁同步电机神经网络逆解耦控制研究[J]．电机与控制学报，2012，16(3)：90-95．

[9]MATTAVELLIP,TUBIANAL,ZIGLIOTTOM.Torque-ripplereductioninPMsynchronousmotordrivesusingrepetitivecurrentcontrol[J].IEEETransactionsonPowerElectronics,2005,20(6):1423-1431.

[10] 朱昊，肖曦，李永东．永磁同步电机转矩预测控制的磁链控制算法[J]．中国电机工程学报，2010，30(21)：86-90．

[11]CHAIS,WANGL,ROGERSE.AcascadeMPCcontrolstructureforaPMSMwithspeedrippleminimization[J].IEEETransactionsonIndustrialElectronics,2013,60(8):2978-2987.

[12]QIANW,PANDASK,XUJX.SpeedrippleminimizationinPMsynchronousmotorusingiterativelearningcontrol[J].IEEETransactionsonEnergyConversion,2005,20(1):53-61..

[13]CHAPMANPL,SUDHOFFSD,WHITCOMBCA.Optimalcurrentcontrolstrategiesforsurface-mountedpermanent-magnetsynchronousmachinedrives[J].IEEETransactionsonEnergyConversion,1999,14(4):1043-1050.

[14] 王东文，栾富刚，宋词，等．大功率永磁同步电机伺服系统的热设计研究[J]．电力电子技术，2013，47(12)：98-100．