分数阶滑模趋近率在SMVS-DTC中的应用

诸德宏，欧阳中萃

(江苏大学，镇江 212013)

0 引 言

永磁同步电机(以下简称PMSM)具有体积小、效率高、可靠性高、易于散热、易于维护等优点,在交流伺服系统中获得广泛应用。直接转矩控制(以下简称DTC)计算量小，响应速度快，对电机参数变化具有一定的鲁棒性，是受欢迎的电机控制方法之一。然而传统的DTC存在系统抖动太大，开关频率不恒定，起动时有较大的冲击电流等缺点。

为解决这些问题，近些年来人们提出了多种方案，如改进空间电压矢量开关表、引入多电平逆变器、滑模变结构控制、自适应控制、模糊控制等。其中，基于滑模变结构的DTC以算法简单、响应速度快、对参数及扰动不灵敏等优点受到诸多关注。文献[1]用两个滑模控制器替代传统DTC中的滞环调节器，来解决以上问题。文献[2]在滑模控制器引入积分项，利用积分滑模面平滑的特性来削弱抖振，同时通过调节初始值的大小，使系统初始状态位于滑模面上，缩减了趋近运动的时间。文献[3-5]用分数阶积分项来替换滑模控制器中的传统的整数阶积分项，利用分数阶系统中旧误差累积会随时间缓慢衰减的特性来抑制传统积分滑模控制器中积分饱和的现象，从而达到提高滑模控制性能目的，但由于滑模变结构技术的应用，会不可避免地存在抖振问题。文献[6]指出了趋近率的不足，分析了传统趋近率产生抖振的本质原因，并设计了两种新型滑模趋近率。文献[7]则以航天器姿态控制系统为控制对象，将分数阶微分方程和传统等速趋近率相结合提出了分数阶趋近率概念，仿真结果显示分数阶趋近率不仅可以柔化系统运动轨迹，减小暂态过程中的超调量，同时还可以改善系统抖振现象。文献[8-9]针对Lorenz电路等不同形式的混沌系统对分数阶趋近率进行一系列的研究。上述文献虽然不同程度地涉及到分数阶趋近率，但还未有专门的文献针对基于分数阶趋近率的滑模控制器在PMSM中的应用特性进行研究。

本文在文献[3-5]分数阶滑模控制器基础上，结合文献[7-9]分数阶趋近率设计一种改进型的分数阶滑模控制器。首先分析了分数阶指数函数曲线特性图，从理论上证明了它的收敛性和平稳性，然后通过和传统的指数趋近率对比仿真来验证这些特性，最后以PMSM为控制对象使用Simulink仿真软件来验证该控制方法的可行性。

1 数学模型

1.1 PMSM数学模型

本文的PMSM采用三相交流电，定子采用星形接法。为方便数学建模，忽略磁路饱和、涡流、磁滞损耗、阻尼绕组以及高次谐波的影响，则PMSM在α-β坐标系下的状态方程：

式中：uα，uβ，iα，iβ分别为α-β坐标系下的定子电压、电流；Ld，Ld分别为d-q坐标系下的等效电感；Rs，ψf分别为定子电阻和永磁体磁链系数；eα，eβ为拓展反电动势[1-3],其值：

α-β坐标系下PMSM转矩方程：

ψαiβ-ψβiα) (3)

θ为转子磁链与x轴之间的夹角；p为电机磁极对数。

1.2 分数阶微积分定义

分数阶微积分是对古典微积分的拓展和延伸，使得古典微积分的阶次从正整数推广到了任意实数乃至复数。大多数情况下，在对实际系统建模过程中，古典微积分只能建立近似的数学模型，而分数阶微积分才能建立更加精准的数学模型[6]。

dtαR(α)>0

1 R(α)=0

式中：a，t分别为微积分的下限和上限;α是微积分的阶次；R(α)为任意复数α的实部。

由于分数阶微积分的特殊性，至今还未有统一的定义，人们根据不同的应用需求和限制条件,推导出了形式不同的分数阶微积分定义，现在主要有Grunwald-Letnikov型、Riemann-Liouville型和Caputo型这3种[10]定义。

1) Grunwald-Letnikov型定义

jf(t-jh) (5)

2) Riemann-Liouville型定义

3) Caputo型定义

本文采用GL型的定义对分数阶滑模趋近率进行数值上的计算，采用C型的定义对分数阶系统微分方程进行数值计算。

GL型定义下的Laplace变换：

L{Dαf(t)}=sαF(s) (8)

式中：F(s)为f(t)的Laplace变换;sα为分数阶微积分算子。

1.3 分数阶指数函数的特性

分数阶微积分最基础的单元形式就是基本分数阶微分方程，对基本分数阶微积分方程求解不仅能够让我们很好的了解其特性，并且在求解其他的分数阶微积分方程具有很重要的意义，还能为改进分数阶滑模控制器提供重要的依据[8]。

所有初始条件为0，并且忽略记忆因素影响的情况下，基本分数阶微分方程：

Dαx(t)=-αx(t)+bu(t) (9)

传递函数：

可以利用下式进行反拉氏变换：

对式(10)反拉普拉斯变换：

并定义：

对式(9)两边同时求Laplace变换：

sαX(s)-x0=-aX(s)+bu(s) (14)

化简：

(sα+a)X(s)=x0+bu(s) (15)

两边同时乘以F(s)进一步化简：

X(s)=F(s)x0+F(s)bu(s) (16)

对式(14)求Laplace逆变换，解得：

式中:x0=[Dα-1x(t)]t=0，可以解出其解析解:

由式(18)通过MATLAB可以得到其解的曲线,如图1所示。

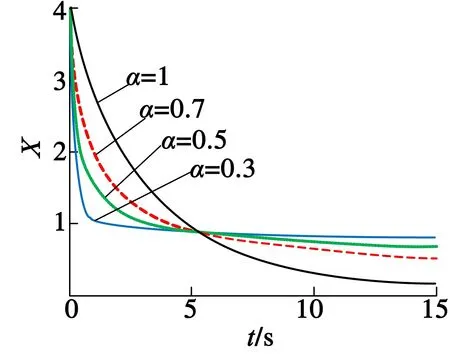
(a)a=-4

(b)α=0.5

图1不同阶次不同系数的解

由图1可以看出，分数阶指数函数曲线形状与整数阶的指数函数曲线形状十分类似，并且当参数a固定时，微分阶次α越小，下降速度越快，趋于稳定时的速度越缓慢，而这正好与趋近率的设计要求一致。

2 分数阶滑模控制器的设计

2.1 趋近率的设计

趋近率作为滑模控制的最基本组成部分之一，反映了系统以何种方式到达滑模面。在趋近过程中，通常希望系统远离滑模面的时候，趋近速度尽可能得快；而在接近滑模面的时候，又希望趋近速度能尽可能地减小为零，以免造成较大的冲击，从而达到抑制抖振的目的。

从分数阶指数函数曲线特性以及分数阶微积分的定义可以看出，分数阶微分方程十分符合这一要求，因此，不难想到将分数阶微分方程和传统指数趋近相结合，与指数趋近率相比，这种趋近率收敛速度应该更快，且更加平滑，后面的仿真结果也证明了这点。现给出分数阶趋近率如下：

Dαs=-ks-εsgn (s)(k>0，ε>0，0<α<1) (19)

2.2 滑模面的设计

s=sT

ss=eT+c1D-α

eψ+c2D-α(20)

式中:c1，c2为分数阶积分系数；α为分数阶积分系数，0<α<1。

选择式(19)的分数阶趋近律：

对sT和sψ分别求导，得：

将式(1)代入式(22)可得：

U1=-B-1A1+F1+D1-α(KTS+εTsgn(s))

A2+F2+D1-α(KψS+εψsgn(s)) (23)

其中：

为了能更清楚的说明分数阶趋近率的有优点，先给出文献[3]中改进前的控制率方程，方便后面的对比仿真。选取传统的指数趋近率：

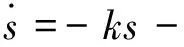
ε·sgn(s)

(27)

同理可得：

其控制率为:

2.3 稳定性分析

sT[D1-α(-kTs-εTsgns)]+

sψ[D1-α(-kψs-εψsgns)] (30)

由式(7)可以推导出：

利用sgn [D1-α(-ks-εsgns)]=-ks-εsgns[7]可以对等式进一步化简：

sgnsT[D1-α(-kTs-εTsgns)]+

sgnsT[D1-α(-kTs-εTsgns)]=

sgns(-kTs-εTsgns)+

sgns(-kψs-εψsgns)=-kTs-

εTsgns·sgns-

kψs-εψsgns·sgns(32)

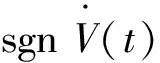
3 仿真分析

为了验证改进后的分数阶滑模控制器的控制性能，将它和改进前的分数阶滑模控制器在Simulink中进行对比仿真。系统控制原理结构框图如图2所示，所用PMSM参数：定子电阻Rs=0.98 Ω；母线电压udc=300 V；极对数p=4；交、直轴电感Ld=Lq=0.008 5 H；转动惯量J=0.008 kg·m2;磁链给定值ψf=0.175 Wb；负载给定转矩T*=10 N·m；转速给定值nN=500 r/min 。

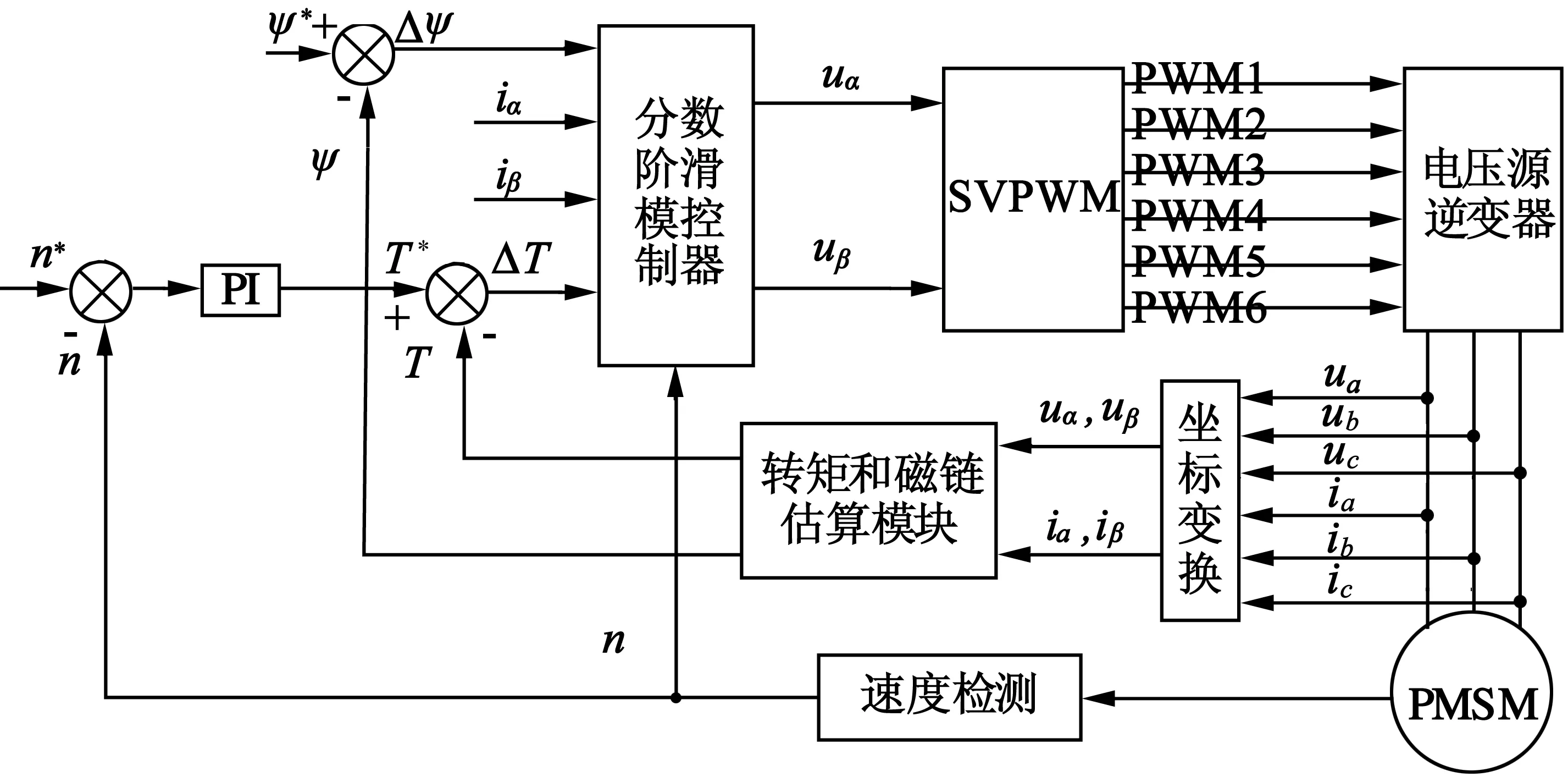
图2基于分数阶趋近率的分数阶滑模变结构系统控制框图

设置电机空载起动，仿真时间为0.2 s，给定磁链ψ*=0.175，给定转速为n*=500 r/min，分数阶阶次λ=0.95。滑模面采用分数阶滑模面，趋近率分别采用指数趋近率和分数阶趋近率来进行对比仿真，图3～图6分别为系统定子磁链轨迹、定子电流波形、转速波形和电磁转矩波形。

(a) 改进前

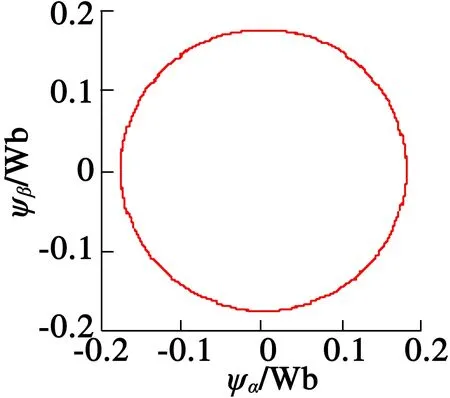
(b) 改进后

图3定子磁链轨迹图

(a) 改进前

(b) 改进后

图4定子电流波形

图5转速曲线

(a) 改进前

(b) 改进后

图6电磁转矩图

从图3～图6可以看出,分数阶滑模面和分数阶趋近率相结合的方法能使系统收敛较快，其转速和转矩波动也比较小。从图4(a)和图4(b)的对比也可以看出,改进后分数阶滑模控制器能使定子电流波形更加平滑。

为了验证动态特性，系统稳定运行后，对给定的负载转矩进行突变，然后观测其运行效果。图7和图8分别是给定的负载转矩在0.1 s时从10 N·m突然增加到15 N·m的转矩响应曲线以及电机转速响应曲线。

图7突加负载时转速响应图

(a) 分数阶滑模DTC

(b) 改进型分数阶滑模DTC

图8突加负载时转矩响应图

从图7、图8可以看出,分数阶滑模面和分数阶趋近率相结合能明显减小转速和转矩脉动，系统响应速度也比改进前的要快。通过对比不难看出,改进后的分数阶滑模控制器对参数突变带来的外部干扰有更好的鲁棒性，具有更好的抗干扰能力。

从以上的仿真结果可以看出，用分数阶趋近率替代传统指数趋近率，构建的新型分数阶滑模控制器，不仅保留了转矩、磁链抖振小等原有的性能，而且还能提高系统收敛速度、减小超调量、柔化了运动轨迹，提高了PMSM调速性能。

4 结 语

改进后的滑模控制器充分利用了分数阶微积分具有微分和积分两个可变的自由度的性质。

在滑模切换面的设计中引入分数阶积分项，利用分数阶积分方程中积分阶次越小，下降速度越快，趋于稳定时的速度越缓慢的性质，不仅保留了原来积分滑模控制器中原有的优点，还很好地抑制传统积分滑模控制器中存在的积分饱和的问题。

在趋近率设计中引入分数阶微分方程，利用分数阶微分特性，使得系统在远离滑模面时能更快地到达滑模面，接近滑模面时趋近速度又比较小，从而抑制因为冲击带来的抖振。

[1] 贾洪平,贺益康.永磁同步电机滑模变结构直接转矩控制[J].电工技术学报,2006,21(1):1-6.

[2] 李政,胡广大,崔家瑞,等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014(3):431-437.

[3] HUANG J,XU Q,SHI X,et al.Direct torque control of PMSM based on fractional order sliding mode variable structure and space vector pulse width modulation[C]// Control Conference.IEEE,2014:8097-8101.

[4] 邓立为.分数阶滑模控制理论及其应用研究[D].哈尔滨:哈尔滨工业大学,2014.

[5] 张碧陶,皮佑国.基于分数阶滑模控制技术的永磁同步电机控制[J].控制理论与应用,2012,29(9):1193-1197.

[6] 孙力.永磁同步电机调速系统滑模变结构控制若干关键问题研究[D].哈尔滨: 哈尔滨工业大学,2014.

[7] 宋申民,邓立为,陈兴林.分数阶微积分在滑模控制中的应用特性[J].中国惯性技术学报,2014(4):439-444.

[8] 顾文军.Lorenz混沌电路的分数阶控制[D].南京:南京林业大学,2012.

[9] AGHABABA M P.Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique[J].Nonlinear Dynamics,2012,69(1-2):247-261.

[10] 张文芳.分数阶微积分概念的起源和演化[D].西安：西北大学,2014.

[11] TEPLJAKOV A,PETLENKOV E,BELIKOV J.FOMCON:Fractional-order modeling and control toolbox for MATLAB[C]//Proceeding of 18th Int Mixed Design of Integrated Circuits and Systems (MIXDES) Conference.2011:684-689.