基于滑模观测器永磁同步电机迭代学习控制

李 晖，刘偲艳，田拥军，兰永红

(1.湖南理工职业技术学院，湘潭 411100;2.湘潭大学，湘潭 411105)

0 引 言

永磁同步电机因其高功率密度、低转动惯量和高效率等特点,在现代工业领域的伺服系统技术中具有广泛应用。但是，转矩脉动的存在制约发展，因此对转矩脉动抑制的研究具有实际意义[1]。近年来，国内外众多学者在永磁同步电机转矩脉动方向开展了很多研究，总体可分为两类[1]：第一类主要考虑从电机设计方向进行优化[2]，使电机参数更理想，从而提高转矩的平滑性，降低转矩脉动。但该类方法对转矩脉动抑制效果有限，电机造价却很大程度增加。第二类主要考虑从电机控制方向进行优化，使控制算法更优，从而抑制脉动分量。文献[3]采取谐波电流注入法，能够实现指令电流的完全跟踪，较好地抑制转矩脉动。文献[4]利用自适应控制技术，在线调整系统参数。文献[5]提出一种在线估计技术的闭环控制算法，较大程度地抑制转矩脉动。但这些方法都依赖于永磁同步电机精确的数学模型。文献[6]提出一种ILC策略，通过重复利用输入输出信息构造产生目标输出的控制信息，从而改善跟踪性能，且不依赖于精确的数学模型。

高阶ILC算法[7]同时利用当前迭代过程输入输出信息和历史信息来构造学习算法，从而得到新的控制输入。与普通学习算法相比，高阶迭代学习算法具有更高的系统收敛速度。

本文在文献[6]的基础上，采用高阶形式，利用历史迭代过程的控制信息，可提高系统收敛性能。

上述控制策略均需要获得精确的转子速度和位置信息，传统传感器测量简单、有效，但增加电机造价、复杂程度，同时易受环境影响，降低可靠度。文献[8-9]提出滑模观测器，能有效估算转子信息，但同时引入抖振。本文设计二阶滑模观测器估算转子位置和转速，可克服传统滑模观测器“抖振”的问题。最后，利用MATLAB/Simulink仿真说明了此方法的有效性。

1 永磁同步电机数学模型

永磁同步电机(面贴式)在同步旋转(d-q)坐标系d，q轴电压方程：

diddt=-RLid+ωeiq+1Lud

(1)

diqdt=-RLiq-ωeid-ψfLωe+1Luq

(2)

式中：id,iq为定子电流d，q分量；ud,uq为定子电压d，q分量；L,R为定子电感、电阻；ωe为转子电角速度；ψf为永磁体磁链。

永磁同步电机转矩方程：

Tm=3p2ψfiq=ktiq

(3)

式中：kt=3p2ψf为转矩系数，p为电机极对数。

永磁同步电机动力学方程：

dωdt=3pψf2Jiq-BJω-TLJ

(4)

式中：J为转动惯量；B为摩擦系数；TL为电机负载转矩；ω为转子机械角速度。

2 迭代学习控制器

为了定性分析二阶迭代学习控制策略，考虑如下动态系统：

x·k+1(t)=Axk+1(t)+Buk+1+f(x)

yk+1(t)=Cxk+1(t)+dk

xk+1(0)=0,t∈[0,T0]

(5)

式中：[0,T0]为运行持续时间；A，B,C分别为相应维数的矩阵，且满足CB≠0；f(x)为非线性量；dk为转矩扰动。由文献[10]可知，所有含微分增益Γd的学习控制策略，其收敛条件都一样，可表示：

ρ=1-ΓdCB<1

(6)

定理1:向量函数f:f(t)=[f1(t)，…，fm(t)]T，t∈[0,T0],那么向量函数f的Lebesgue-p范数[11]：

(7)

由文献[12]可以知道,limp→∞‖f(·)‖=‖f(·)‖∞=‖f(·)‖sup。

2.1 二阶迭代学习控制器

假设yd(t),t∈[0,T0]为目标输出，构造二阶PD型ILC (L(c1,c2))如下：

u2(t)=u1(t)+Γp1e1(t)+Γd1e·1(t)

uk+1(t)=c1[uk(t)+Γp1ek(t)+Γd1e·k(t)]+

c2[uk-1(t)+Γp2ek-1(t)+Γd2e·k-1(t)]

(8)

ρ1=‖1-Γd1CB‖<1

ρ2=‖1-Γd2CB‖<1

(9)

第k+1次迭代系统跟踪误差ek+1(t)可表示：

‖ek+1(·)‖p=c1ρ1‖ek(·)‖p+c2ρ2‖ek-1(·)‖p

(10)

所以，limk→∞‖ek+1(·)‖p=0，二阶迭代学习控制算法收敛。证明系统在有限时间内能够收敛，下面将对收敛速度进行分析。

2.2 一阶迭代学习控制器

假设式(8)中c1=1，控制律退化为一阶PD型ILC(L(1))，表达式如下：

uk+1(t)=uk(t)+Γp1ek(t)+Γd1e·k(t)

t∈[0,T0]，k=1,2,3,…

(11)

式中：Γp1，Γd1，uk(t),ek(t)与式(8)一样，结合电机动力学式(4)和PD-ILC的收敛条件式(6)，可得一阶迭代学习控制算法的收敛条件：

ρ1=1-Γd1CB<1

(12)

第k+1次迭代系统跟踪误差ek+1(t)可表示：

‖ek+1(·)‖p=ρ1‖ek(·)‖p

(13)

所以，可得limk→∞‖ek+1(·)‖p=0，一阶迭代学习控制算法收敛。

3 收敛速度对比

令limk→∞‖ek+1(·)‖p‖ek(·)‖=ρ，由文献[12]可得ρ值大小与系统跟踪误差收敛速度成反比，这样，可通过比较ρ值的大小来判断L(1),L(c1,c2)收敛速度的快慢。令L(1),L(c1,c2)的ρ值分别为ρ[L(1)]，ρ[L(c1,c2)]。式(10)两边同时除以‖ek(·)‖p，并取极限可得：

ρ2-c1ρ1ρ-c2ρ2≤0

(14)

那么，式(14)解的范围：

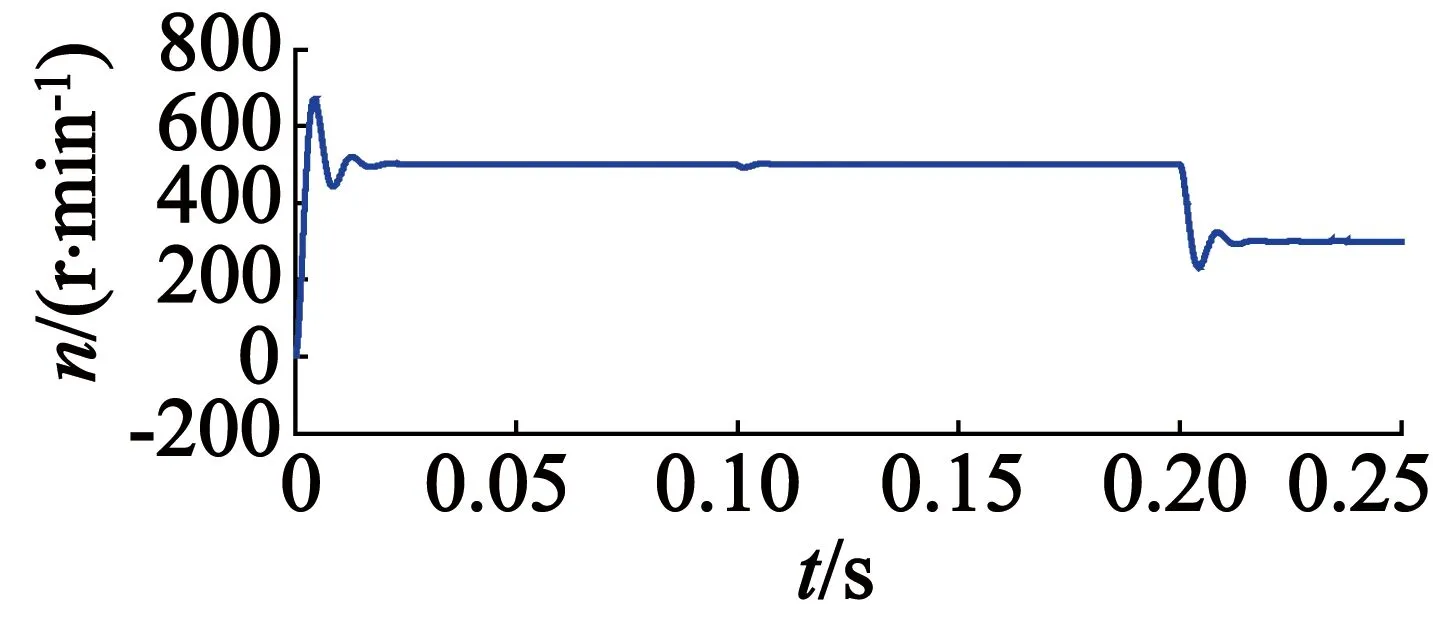
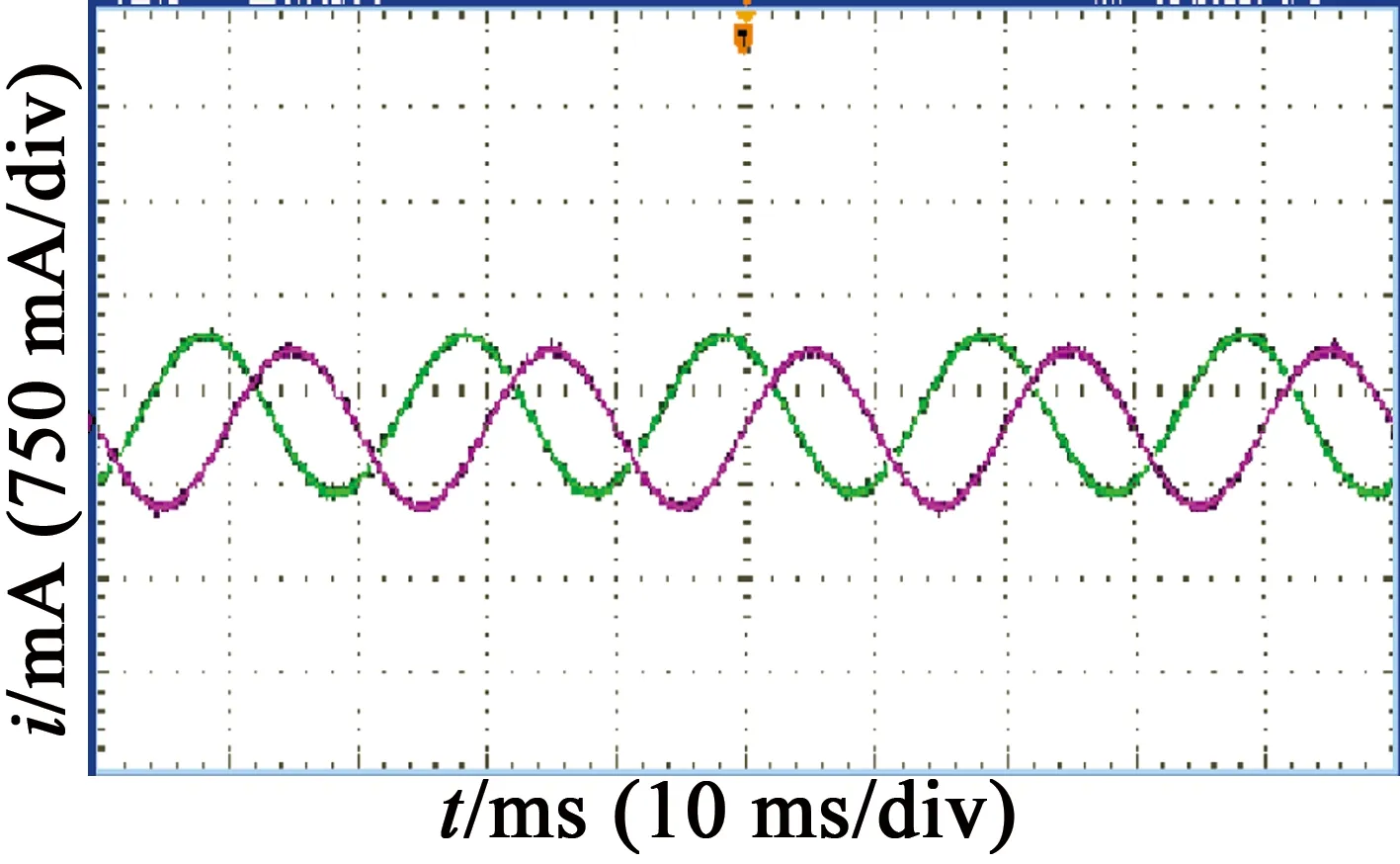
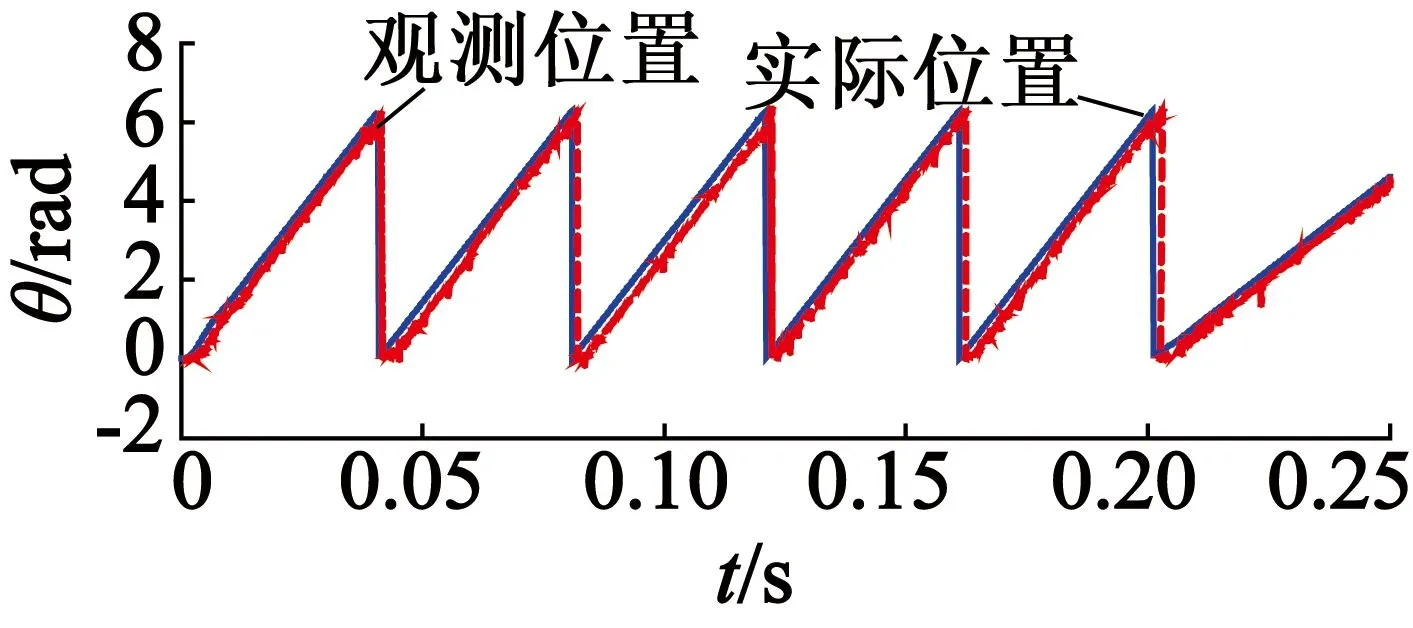
c1ρ1-(c1ρ1)2+4c2ρ22<ρ

(15)

由于c1+c2=1，又ρ>0。则上述不等式等价于0<ρ

F(c1)=c1ρ1+(c1ρ1)2+4c2ρ22,0

(16)

对F(c1)进行微分可得：

(17)

ρ1(c1ρ1)2+4ρ2(1-c1)=

即F′(c1)>0，可得：F(c1)min=ρ2,F(c1)max=ρ1。

所以ρ[L(c1,c2)]=F(c1)<ρ1=ρ[L(1)]，证明L(c1,c2)误差收敛速度比L(1)快。

F(c1)min=F(1)=ρ1

F(c1)max=F(0)=ρ2

(19)

所以，ρ[L(c1,c2)]=F(c1)>ρ1=ρ[L(1)]，证明L(c1,c2)误差收敛速度比L(1)慢。

从上述分析可得，比例增益Γp1，Γp2和微分增益Γd1，Γd2的值决定不同的ρ1,ρ2的值，决定L(c1,c2)收敛速度与L(1)收敛速度的关系。

4 二阶滑模观测器设计

在静止α-β系，永磁同步电机模型[13]：

i^α=-Riα-eα+uαL

i^β=-Riβ-eβ+uβL

(20)

式中：iα,iβ为定子电流;uα,uβ为定子电压;eα,eβ为反电动势。

eα=-ψfωesinθe

eβ=-ψfωecosθe

(21)

式(21)为α-β坐标系PMSM数学模型。利用该数学模型设计二阶滑模观测器如下：

i^·s=-Ri^s+us+zL

(22)

结构框图如图1所示。

图1二阶滑模观测器结构框图

式(22)中：i^s=[i^α,i^β]是is=[iα,iβ]的估算值；us=[uα,uβ]；z=[zα,zβ]。由式(20)、式(22)相减可得到电流估算误差表达式：

s·s=i^·s-i·s=-RssL+esL+zL

(23)

式中：ss=[sα,sβ]为电流估算误差；sα=i^α-iα，sβ=i^β-iβ；es=[eα,eβ]。

设计滑模面：

式中：k1,k2分别为滑模面比例、积分增益。

定理2：若根据式(23)系统误差状态方程设计滑模面为式(24)，式(25)、式(26)、式(27)是所设计的滑模控制律，那么，定子电流估算误差i^s=[i^α,i^β]为零，二阶滑模观测能有效地估算转子位置和转速，系统收敛。

z=zeq+zsw

(25)

式中：zeq,zsw分别为等效控制算法和切换控制算法。等效控制应满足条件S·=0,结合式(24)可得：

zeq=-k2k1Lss+Rss-es

(26)

zsw=Lksgn(S)

(27)

证明：系统Lyapunov函数定义：

V=12S2

(28)

对式(28)求导可得：V·=S·S

SS·=S[k1ss+k2ss]=

Sk1L[-Rss+es-k2k1Lss+Rss-esLksgn(S)]+k2ss=

S[k1k2sgn(S)]=k1kS

(29)

当k1k<0时，则V·<0。二阶滑模控制满足S=S·=0，系统收敛。反电动势可表示：e^α=-zα,e^β=-zβ。

故永磁同步电机转子位置观测值：

θ^e=-arctaneαeβ=-arctanzαzβ

(30)

可推算出转子转速观测值：

(31)

5 系统仿真

采用二阶PD型迭代学习控制产生q轴补偿电流，结构框图如图2所示，永磁同步电机参数选取如表1所示。

在仿真试验中参数设计：Γp1=0.8,Γd1=0.01，Γp2=0.3，Γd2=0.006，加权系数c1=c2=0.5，k1=1,k2=15,k=30 000。MATLAB/Simulink参数设定：PMSM起始目标速度值500 r/min，0.2 s目标速度设定为300 r/min。PMSM起始目标转矩5 N·m，0.1 s目标转矩设定为10 N·m。

图2系统控制结构框图

表1永磁同步电机参数

参数值参数值定子电阻R/Ω0．56极对数p3转动惯量J/(kg·m2)0．0021永磁磁通Ψf/Wb0．82定子电感L/H0．0153粘滞摩擦系数B0．0001

图3表示采用二阶PD型迭代算法时系统的输出响应图，图4表示采用一阶学习算法时系统输出响应图。在扰动情况下，二阶迭代学习控制在0.1s时刻转矩增至10N·m，能准确跟踪外部目标值；0.2s时刻转速降为300r/min，转矩收敛速度快于一阶迭代学习控制，三相定子电流脉动值小于一阶迭代学习控制。

(a) 三相定子电流

(b) 转速(c) 电磁转矩

图3二阶ILC控制系统仿真图

(a) 三相定子电流

(b) 转速(c) 电磁转矩

图4一阶ILC控制系统仿真图

在如图5所示的实验平台上进行实验，实验结果如图6所示。图6(a)转速为500r/min时相应转子两相电流波形，图6(b)此时定子电压波形，图6(c)为电机位置估计的波形。

图5实验平台

(a) 两相电流波形

(b) 定子电压波形(c) 电机位置估计波形

图6实验结果

6 结 语

本文根据永磁同步电机的周期性脉动问题，提出一种二阶ILC策略，利用Lebesque-p范数对系统误差的收敛情况进行分析，然后与传统迭代学习算法进行对比，并分析误差收敛速度与比例、微分设置的关系。另外提出二阶滑模观测器估算电机转子位置与转速，通过配置不同增益可获得快速的收敛速度。

[1]JAHNSTM,SOONGWL.PulsatingtorqueminimizationtechniquesforpermanentmagnetACmotordrives-areview[J].IEEETransactionsonIndustrialElectronics,1996,43(2):321-330.

[2]CHUWQ,ZHUZQ.Investigationoftorqueripplesinpermanentmagnetsynchronousmachineswithskewing[J].IEEETransactionsonMagnetics,2013,49(3):1211-1220.

[3]LIZhixin,CHENZhenfei，AlShufeng.Torqueripplereductionfornon-sinusoidalback-EMFpermanentmagnetsynchronousmachineswithcurrentharmonics[J].2016 19thInternationalConferenceonElectricalMachinesandSystems(ICEMS),Chiba,2016:1-4.

[4]DongQuangDang,MuhammadSaadRafaq,HanHoChoial.OnlineParameterEstimationTechniqueforAdaptiveControlApplicationsofInteriorPMSynchronousMotorDrives[J].IEEETransactionsonIndustrialElectronics,2016,63(3):1438-1449,.

[5]XUY,PARSPOURN,VOLLMERU.Torquerippleminimizationusingonlineestimationofthestatorresistanceswithconsiderationofmagneticsaturation[J].IEEETransactionsonIndustrialElectronics,2014,61(9):5105-5114.

[6] 孙明轩,毕宏博,周国良,等.反馈辅助PD型迭代学习控制:初值问题及修正策略[J].自动化学报,2015,(1):157-164.

[7] 逄勃,邵诚.高阶参数优化迭代学习控制算法[J].控制理论与应用,2015(4):561-567

[8] 亓立锋,杨淑英,张兴,等.基于滑模观测器的PMSM无速度传感器控制[J].电力电子技术,2016,(1):102-104+108.

[9] 史婷娜,肖竹欣,肖有文,等.基于改进型滑模观测器的无刷直流电机无位置传感器控制[J].中国电机工程学报,2015(8):2043-2051.

[10] OUYANG P R,PIPATPAIBUL P I.Iterative learning control:a comparison study[C]//ASME 2010 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers,2010:939-945.

[11] PINSKY M A.Introduction to Fourier analysis and wavelets[J].Graduate Studies in Mathematics,2009,32(9):376.

[12] XU J X,TAN Y.Robust optimal design and convergence properties analysis of iterative learning control approaches[J].Automatica, 2002,38(11):1867-1880.

[13] 鲁家栋,刘景林,卫丽超.永磁同步电机转子初始位置检测方法[J].电工技术学报,2015,(7):105-111.