一种改进的K-均值聚类算法∗

隋心怡 王瑞刚 张鸿翔

（1.西安邮电大学计算机学院 西安 710061）（2.西安交通大学电子与信息工程学院 西安 710049）

1 引言

聚类问题是指依据样本的某些属性或按照某种标准，将样本分为多个类，并使相同类中的样本相似度尽可能大，不同类中的样本相似度尽可能小［1］。为解决聚类问题，研究人员提出了多种聚类算法，主要有：基于划分的算法、基于层次的算法、基于密度的算法、基于网络的算法、基于模型的算法以及其他形式的算法［2～5］。

基于划分的聚类算法是最早提出，也是最常用的经典聚类算法［6］。该类算法通过选择k个初始聚类中心（代表k个类），然后根据其他样本与中心点的距离，将每个样本划分到与它距离最近的类中，从而实现样本聚类［7］。

K-均值聚类算法就是一种基于划分的聚类算法［8］，由于其原理简单易于实现，在多个领域中都有广泛的应用。但是传统的K-均值聚类算法易受初始点影响，当初始点选择不当时，甚至无法得到正确聚类结果［9～10］，算法稳定性较差。鉴于K-均值聚类算法存在的缺陷，如何选取聚类初始点一直是其算法改进的重要方向［11］。

本文根据样本的空间分布动态选取初始聚类中心，提出了一种改进的K-均值聚类算法。实验结果表明，改进后的算法提高了稳定性，并取得了较高的分类准确率。

2 K-均值聚类算法

K-均值聚类算法首先需要输入聚类个数k，然后随机选择k个样本作为聚类中心；通过计算剩余样本与聚类中心的距离，将样本归入与其距离最近的类；当所有样本计算结束后，根据当前聚类结果更新聚类中心；通过循环迭代直到目标函数［12］满足一定要求或达到最大迭代次数时聚类结束。

目标函数用于度量聚类结果的好坏，其定义如下

K-均值聚类算法常采用欧氏距离［13］表示样本与聚类中心的远近，此时目标函数也称为平方误差准则函数：

当一次迭代结束后，需要更新聚类中心，更新公式为

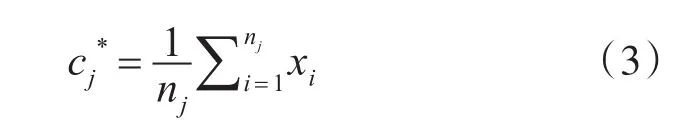
式中nj为第 j类中的样本个数，cj*为新的聚类中心。

算法流程：

1）从样本中随机选取k个对象作为初始聚类中心；

2）计算样本与k个聚类中心的距离，将样本归入距离最近的类中；

3）根据式（3）计算新的聚类中心；

客观原因主要包括：由于温度变化而引起变形、地基地质构造存在较大差别、地下水位上升或降低导致高速公路地基被侵蚀、土壤物理性质存在较大差异，以上各项客观因素都会对造成软土地基发生沉降，从而会对高速公路最终质量造成较为严重的影响，影响高速公路施工，以及工程竣工后的应用。

4）重复步骤2）、3），直至满足结束条件；

5）计算结束，得到聚类结果。

3 改进的K-均值聚类算法

初始聚类中心的选择直接影响到K-均值聚类算法的性能，这导致传统的K-均值聚类算法性能较不稳定［14］。一方面，若随机选取的初始聚类中心距离较近，会导致算法迭代次数较多甚至聚类出现偏差，因为距离较近的两个样本更有可能属于同一类而不是不同类，所以选取相互之间距离较远的k个样本作为初始点更具有代表性；另一方面，若一味地寻找相距较远的初始点，有可能会取到孤立点，也不利于聚类。通过观察数据样本的空间分布发现，实际的聚类中心所在的区域往往密度较高，即这一区域内的样本数量要大于其他区域。针对上述先验知识，本文改进了初始聚类中心的选取方法，根据样本所在空间的分布密度，并结合样本间最大距离选取初始聚类中心。

设待聚类的m个n维数据样本为X，所处空间范围为RN，可表示为

定义子空间r（r∈RN）的样本密度为该子空间内的样本数量，记作ρr。如果一个子空间的样本密度不小于ρmin，则该子空间为高密度子空间，ρmin为高密度子空间阈值。

两个 n维数据 x1(α1，α2，…，αn)、x2(β1，β2，…，βn)间的距离定义为

改进后的K-均值聚类算法流程如下：

1）设定聚类个数k、高密度子空间阈值ρmin；

2）选定正整数l，将输入样本所处的n维空间等分为ln（ln＞2k）个子空间，计算各子空间ri的样本密度 ρri，并将密度不小于ρmin的子空间放入高密度子空间集合Dρ，统计高密度子空间数量；

3）若高密度子空间数量小于聚类个数k，返回1），调整阈值 ρmin；

4）选取密度最高的子空间，计算该空间内样本点的平均距离，设为第一个初始聚类中心c1；

5）计算c1与其他高密度子空间中心的距离，选取与其距离最远的高密度子空间，计算该空间内样本点的平均距离，得到第二个初始聚类中心c2；

6）计算c1、c2与其他高密度子空间中心的距离和，按照最大距离准则选取高密度子空间，并计算得到聚类中心c3；

7）继续按照6）的方法寻找聚类中心，直到找到第k个聚类中心ck；

8）将k个初始聚类中心带入传统的K-均值聚类算法进行聚类，得到聚类结果。

4 实验结果及分析

本文使用UCI机器学习数据库［15］对传统k均值算法和改进算法进行对比实验。选取Iris、Wine和Glass三组数据作为测试数据集。为了使结果更加直观，首先将三个测试数据集不同属性值做归一化处理，并其降维至二维空间。

采用传统k均值算法进行30次实验，取平均值作为实验最终结果；由于改进算法计算出的初始聚类中心是固定的，所以只进行一次试验，并将其结果作为最终结果。实验结果如表1所示。

由表1可以看出，采用本文提出的改进算法得到的聚类精度要好于传统的k均值算法。

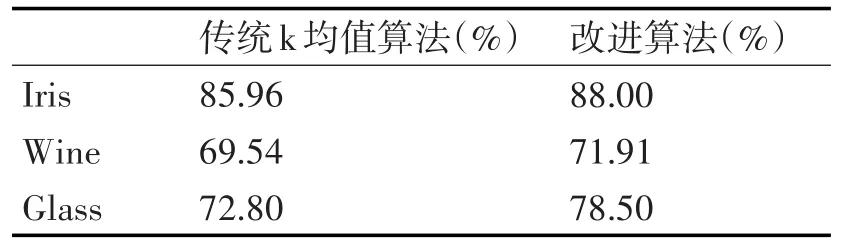
表1 算法精度比较

为对比两算法的运算效率，实验还统计了算法的迭代次数和运行时间，结果如表2所示。由于本文提出的改进算法根据样本点的空间分布选取初始聚类中心，算法迭代次数要明显少于传统k均值算法；但因为改进算法要统计所有样本点的空间分布，会牺牲一定的时间，所以改进算法的运行时间要大于传统的k均值算法。

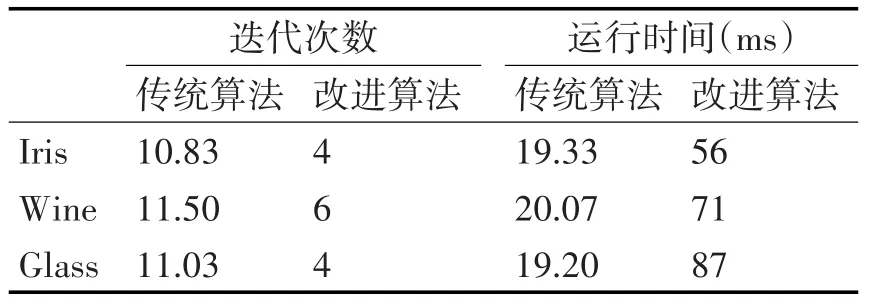
表2 算法迭代次数与运行时间比较

此外，通过观察采用传统k均值算法进行的30次实验，发现各实验间结果相差较大，这也表明由于传统k均值算法的初始聚类中心是随机选择的，结果随机性较强，算法稳定性较差。而本文提出的改进算法在参数设置确定的情况下，实验结果也是固定的，稳定性好于传统k均值算法。

5 结语

本文在传统K-均值聚类算法的基础上，将样本点分布密度与初始点选取相结合，提出了一种改进的K-均值聚类算法，实验结果表明，本算法的聚类精度和稳定性都要好于传统的K-均值聚类算法。

由于本文提出的算法需要分割样本所处的n维空间，当样本属性值较多时，会导致分割得到的子空间数量较多，不利于之后的处理。所以本算法适用于对属性值较少的数据集进行聚类；当属性值较多时，需要先进行预处理，舍弃部分相关属性或将属性值投影到低维空间，然后再使用本算法进行聚类。此外，算法中的参数会影响数据集的聚类效果，如何针对不同数据集设置合理的参数也是今后的研究方向之一。

［1］李桂林，陈晓云.关于聚类分析中相似度的讨论［J］.计算机工程与应用，2004，40（31）：64-65.LI Guilin，CHEN Xiaoyun.The Discussion on the Similar⁃ity of Cluster Analysis［J］.Computer Engineering and Ap⁃plications，2004，40（31）：64-65.

［2］席景科，谭海樵.空间聚类分析及评价方法［J］.计算机工程与设计，2009，30（7）：1712-1715.XI Jingke，TAN Haiqiao.Spatial clustering analysis and its evaluation［J］.Computer Engineering and Design，2009，30（7）：1712-1715.

［3］贾瑷玮.基于划分的聚类算法研究综述［J］.电子设计工程，2014（23）：38-41.JIA Aiwei.Survey on partitional clustering algorithms［J］.Electronic Design Engineering，2014（23）：38-41.

［4］李新良.基于层次聚类算法的改进研究［J］.软件导刊，2007（19）：141-142.LI Xinliang.Improved Research of Hierarchical Cluster Algorithm［J］.Software Guide，2007（19）：141-142.

［5］罗军锋，锁志海.一种基于密度的k-means聚类算法［J］.微电子学与计算机，2014（10）：28-31.LUO Junfeng，SUO Zhihai.A Density Based k-means Clustering Algorithm［J］.Microelectronics&Computer，2014（10）：28-31.

［6］尹成祥，张宏军，张睿，等.一种改进的K-Means算法［J］.计算机技术与发展，2014（10）：30-33.YI Chengxiang，ZHANG Hongjun，ZHANG Rui，et al.An Improved K-means Algorithm［J］.Computer Applications，2014（10）：30-33.

［7］段桂芹.基于均值与最大距离乘积的初始聚类中心优化K-means算法［J］.计算机与数字工程，2015（3）：379-382.DUAN Guiqin.Automatic Generation Cloud Optimization Based on Genetic Algorithm［J］.Computer&Digital Engi⁃neering，2015（3）：379-382.

［8］王千，王成，冯振元，等.K-means聚类算法研究综述［J］.电子设计工程，2012，20（7）：21-24.WANG Qian，WANG Cheng，FENG Zhenyuan，et al.Re⁃view of K-means clustering algorithm［J］.Electronic De⁃sign Engineering，2012，20（7）：21-24.

［9］胡伟.改进的层次K均值聚类算法［J］.计算机工程与应用，2013，49（2）：157-159.HU Wei.Improved hierarchical K-means clustering algo⁃rithm.Computer Engineering and Applications［J］.2013，49（2：157-159.

［10］郑丹，王潜平.K-means初始聚类中心的选择算法［J］.计算机应用，2012，32（8）：2186-2188.ZHENG Dan，WANG Qianpin.Selection algorithm for K-means initial clustering center［J］.Journal of Comput⁃er Applications，2012，32（8）：2186-2188.

［11］王晓燕.常用的聚类算法及改进算法的研究［J］.办公自动化：学术版，2013，3（9）：49-52.WANG Xiaoyan.Commonly Used Clustering Algorithm and Improved Algorithm Research［J］.Office Automa⁃tion，2013，3（9）：49-52.

［12］Meng Jianliang，Shang Hai kun，Bian Ling.The applica⁃tion on intrusion detection based on K-means cluster al⁃gorithm［C］.International Forum on Information Technol⁃ogy and Applications，2009：150-152.

［13］Liu X M，Lei D.An improved K-Means clustering algo⁃rithm［J］.Journal of Networks，2014，9（1）：1-3.

［14］Wu J.K-means Based Consensus Clustering［J］.Knowl⁃edge&Data Engineering IEEE Transactions on，2015，27（1）：155-169.

［15］University B I.Uci machine learning.ftp.ics.uci.edu/pub/machine-learning-databases［J］.2010.