基于SIR模型的情感网络传播分析∗

徐沛东 马 力 李 培

（西安邮电大学计算机学院 西安 710061）

1 引言

情感是人类智能或认知的重要标志，是驱动人类行为发生的一种内在的心理动因，它影响着人们的决策、学习和交流，并在人们的决策行为中起重要甚至决定性作用，它使人类在解决问题时更富有创造性和灵活性。认知心理学研究表明：人们的信息交流行为是受情感影响的。真实社会中人们的情感随其行为表达出来，并通过社会关系链而传递。

在线社交网络上人们的情感随其的网上操作行为表达出来，并通过不同类别的好友圈的互动而传播，进而影响整个朋友圈。正向的情感有助于传播正能量，给人们带来愉快、满足和幸福的感觉，促进社会和谐与进步。而负向的情感则使人们产生不快、愤怒和恐怖的感觉，形成社会不稳定情绪的蔓延，甚至带来社会的动荡。因此，研究社交网络应用中群体情感形成与涌现的原因，分析群体网络行为与情感产生和传播之间的影响关系，研究群体的情感发现、情感计算方法、情感传播机理与情感演化动力学模型，对于舆情监控，产品营销，公共事件评论等公共媒体关注事件有着基础性的作用。

大量的用户使用使得每一天都会产生高达上亿的信息，这些海量的信息包含了用户的各种观点与情感信息，个人和组织越来越多地把网络情感观点信息用于决策，所以研究这些文本信息对于观察分析人们对于社会各种现象的不同观点立场有着非常重要的现实意义。目前大部分在线社交网络情感研究都着重研究文本的情感分析，而忽视了情感在网络的传播分析，随着情感分析的不断深入研究和延伸，情感传播这一研究课题在近些年来开始展开。情感传播研究是一个涉及了文本分析、复杂网络、信息检索、传播学、心理学等多个领域的研究课题。本文基于传统的病毒传播模型SIR对于构建情感网络的传播这一问题进行分析。

2 复杂网络的SIR舆情传播

自然科学、社会科学、工程技术和管理科学等领域能够很好地描述互相关联的复杂模型。以计算机、数学、统计物理学等科学为分析工具，把复杂的系统作为研究目标。复杂网络简单地说就是高度复杂的网络，没有一个严格上的定义，目前普遍采用钱学森给出过的一个描述性的定义：具有自组织、自相似、吸引力、小世界、无标度中部分或者全部性质的网络称之为复杂网络［1］。

复杂网络一般描述为图（graph）。用图结构表示一个复杂网络图G=（V，E）是一种含有“节点”（nodes或者 vertices）的集合 V和“边”（links或者edges）的集合E的数学结构。其中集合E的元素为不同节点的无序组合｛u，v｝，表示节点之间的关系（其中 u，v∈V）。如果不区分 edges（u，v）和 edges（u，v）的两者关系，则称该网络图为无向网络图，否则就成为有向网络图。

舆情传播的的动力学模型符合经典的SIR病毒传播模型［2］，一般网络上的节点被划分成了三种状态：

1）S状态为没有接受过消息的节点（Igorants），类似于病毒传播的易感染节点（Sueceptile），表示不知道消息的个体。

2）I状态为消息传播节点（Spreaders），类似于病毒传播的易感染节点（Infected），表示知道消息并且可以传播的个体。

图1 经典SIR舆情传播图

3）R状态为接受消息但不传播的节点（Sti⁃flers），类似于病毒传播的免疫节点（Remove），对应知道消息但已失去传播能力或者兴趣的个体。

假设网络有N个节点，每一个节点就代表一个可以传播信息的个体，节点之间传播信息的方式有如下方式［3］：如果一个节点得到一则消息并且该节点有兴趣传播给其他节点（I状态），传播过程该节点随机地从相邻节点选取节点进行消息传递，如果该相邻节点并未知晓该消息（S状态），则该节点就接收到消息（I状态），并进行下一次传播。如果该节点事先知道该一消息并且没有兴趣继续传递则变成不传播状态（R状态）。不同个体之间的传播概率存在差异，不同拓扑结构的社会网络传播规律也不相同。

3 基于SIR的情感网络传播模型

3.1 情感网络传播机制与模型

基于上文介绍社交网络复杂网络理论，采用图的概念来构建情感网络。定义情感网络图结构：用图结构表示，一个情感网络图G=（V，E，P），其中V表示情感网络中所有节点的结合（nodes），E表示为情感网络中所有节点之间连接关系的集合（edg⁃es），而P则用来表示情感网络中每个节点情感的属性（emotion）。

定义情感网络个体情感属性类别：在情感网络图G=（V，E，P）中，P表达的属性分为三种情感可能正向情感（Positive emotion）、负向情感（negative emotion）、中性情感（neutral emotions）。即在一个情感网络中某一个节点的情感属性只能是上述定义的三种情感之一［4］。

基于上文介绍的SIR舆情传播模型基础上提出基于SIR的情感传播模型［5］，重新定义S状态、I状态、R状态在情感传播中意义如下：

1）S状态为没有有任何情感的特征，默认的设定为节点的情感处于中性情感状态。

2）I状态为个体受到情感刺激具有了情感情绪，此时节点的情感呈现正向情感状态或者负向情感状态之一，并且节点的情感状态具有传播给下一节点的可能。

3）R状态为接受到其他节点的情感传递，但情感的属性在该节点发生了反向转变，从接受的正向情感转换为了负向情感或者负向情感转换为了正向情感，并且节点的情感状态具有传播给下一节点的可能。

情感网络中初始S状态有若干个体受到情感刺激转变为I状态，记α为I状态向相邻S状态个体刺激并使之变为I状态的概率，β为I状态向相邻S状态个体刺激并使之变为R状态的概率，λ为R状态向相邻S状态个体刺激并使之变为R状态的概率，其中α≫β。

因此情感网络的传播模型可以使用如下图的不同节点之间的状态转移图表示。

图2 情感网络传播模型图

针对上述所提出的转移状态模型，令s(t)，i(t)，r(t)分别代表着t时刻S态、I态、R态节点在情感网络中的个体密度，N为系统个体总数，则情感网络中I态的个体密度随时间的变化率为［6］

情感网络中R态的个体密度随时间的变化率为

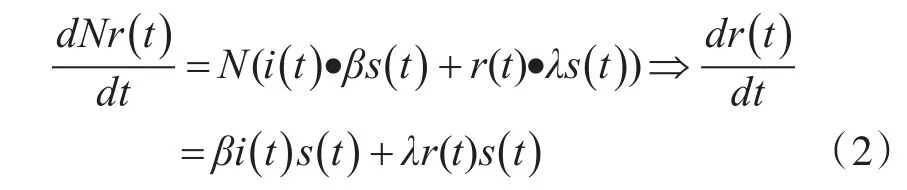
由于s(t)+i(t)+r(t)=1，情感网络中S态的个体密度随时间的变化率为

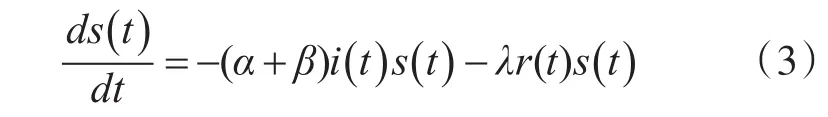
推出基于SIR情感网络传播的动力学行为可以用如下微分方程描述：

在上式中，第一个方程式表示了S状态中性情感节点的变化率；第二个式子则表示了受到情感刺激I状态情感节点的变化率；最后的第三个式子表示了情感传播过程情感发生反向转移的R状态节点变化率。

3.2 模型仿真与分析

在上文所建立的情感网络传播模型当中，引入了三个概率参数，α为中性情感受到刺激变为主要情感类型的传播概率，β为节点发生反向情感转移概率，λ为反向情感发生持续传播概率。下面将给出基于基于SIR的情感网络传播模型的仿真结果［7～8］，分析不同类型节点在传播过程当中节点密度的变化规律。

图3 情感网络传播模型仿真结果

上图给出了分别代表着t时刻S态、I态、R态节点在情感网络中的个体密度的s（t），i（t）和r（t）随时间t变化的曲线。在仿真时给定了s（0）=0.98和i（0）=0.02的初始值，令α=0.3，β=0.02，λ=0.2。在情感网络中所有节点最后都会被感染成为具有情感倾向的节点，有图可以看出S状态节点的密度会呈现由慢到快咱变慢的速率逐步下降受到感染转变为其他状态，I与R状态节点密度与S状态节点成相反趋势，而I状态节点密度会大幅度增大，R状态节点密度感染概率所占比例非常的小，最大幅度的状态转移在t为15左右的时间段发生，大约在t大于30之后三种状态节点的密度区域稳定不在发生转移。

4 基于社交网络的情感传播模拟

选取目前我国应用最为广泛的社交网络新浪微博240名用户关系数据作为模拟数据［9］，把微博注册用户看作为情感网络节点，用户之间的好友关系表示为连接节点的边，用户对于同一事件的情感态度作为节点的情感属性，从而构建了具有现实参考的情感传播网络图G=（V，E，P）。如图4（a）利用R语言模拟出所有用户的可视化关系网络图，图4（b）表示保留主要用户关系利用Kamada-Kawai算法生成出的可视化主要关系网络图［10］。

图4 微博用户关系网络图（a）与主要关系图（b）

利用上文提出的情感传播模型在社交网络进行情感传播模拟仿真，选用在仿真时给定了s（0）=0.98和i（0）=0.02的初始值，令α=0.3，β=0.02，λ=0.2。所以给定初始随机有5个节点受到了正性的情感刺激（深色），其余节点都是中性情感节点（浅色），所以如图5（a）在t=0时，有5个节点受到刺激；图5（b）表示在t=10时，正性情感的节点开始大范围增多，并且有反向负性情感出现（黑色）［11］。

图5 情感传播可视化图t=0（a）与t=10（b）

图6（a）表示在t=20时，正向情感基本已经完成传播传播过程，中性情感剩下的节点已经不多，负向情感节点也有一定程度增长；图6（b）表示在t=30时，传播基本已经完成，中性情感节点基本没有，正负向情感按照大比例在网络节点中分布。

图6 情感传播可视化图t=20（a）与t=30（b）

该微博社交网络用户的模拟情感传播过程基本符合了情感网络传播的仿真趋势，说明了在现实的情感传播过程中主要情感在传播过程中占到主导地位，清楚地表示了情感网络在情感传播中的个体情感变化过程。

5 结语

本文基于复杂网络的一般描述图论提出了情感网络图的概念，基于SIR舆情传播模型改进提出了基于SIR的情感传播模型，并对模型进行了动力学方程描述仿真，说明了情感在网络传播过程的状态的变化过程，最后基于现实微博用户数据进行传播过程验证。但对于有向网络的情感网络传播研究不够，未来拟对于具有方向性的传播过程进行更深入研究。

［1］Zhou Tao，Fu Zhongqian，Niu Yongwei，etc.On the com⁃plex network transmission dynamics research review［J］.Progress in natural science，2005，15（5）：513-518.

［2］丁兆云，贾焰，周斌，等.社交网络影响力研究综述［J］.计算机科学，2014，41（1）：48-53.DING Zhaoyun，JIA Yan，ZHOU Bing，et al.Survey of In⁃fluence Analysis for Social Networks［J］.Computer Sci⁃ence，2014，41（1）：48-53.

［3］ Barrat A，Barthlemy M，Vespignani A.Dynamical pro⁃cesses on complex networks［J］.2008（3）.

［4］马力，宫玉龙.文本情感分析研究综述［J］.电子科技，2014，27（11）：180.MA Li，GONG Yulong.Research on the Text Sentiment Analysis［J］.Electronic Sci.&Tech，2014，27（11）：180.

［5］An Analysis of Knowledge Chain Based on Social Network Theory［J］.Journal of Information，2007.

［6］Earn D J D.Mathematical epidemiology of infectious dis⁃eases［J］.Mathematical Biology，2009：153-186.

［7］Jeong B H，Mason.SP，Barabasi AL，Oltvai ZN.2001.Lethality and centrality in protein networks.Nature 411：41-42［J］.2015.

［8］Wu F，Huberman B A，Adamic L A，et al.Information flow in social groups［J］.Physica A Statistical Mechanics&Its Applications，2003，337（1-2）：327-335.

［9］曹玖新，吴江林，石伟，等.新浪微博网信息传播分析与预测［J］.计算机学报，2014（4）：779-790.CAO Jiuxin，WU Jianglin，SHI Wei，et al.Sina Microblog Information Diffusion Analysis and Prediction［J］.Chinese Journal of Computers，2014（4）：779-790.

［10］Kamada T，Kawai S.An algorithm for drawing general undirected graphs［J］.Information Processing Letters，1989，31（1）：7-15.

［11］Krivitsky P N，Handcock M S.A Separable Model for Dy⁃namic Networks.［J］.Journal of the Royal Statistical Soci⁃ety，2014，76（1）：29-46.