基于蜂群优化神经网络的环境空气质量预测∗
2018-04-26刘笃晋蒲国林王光琼
刘笃晋 蒲国林 王光琼
(四川文理学院智能制造学院 达州 635000)
1 引言
当前以可吸入颗粒物(PM10,PM2.5)、一氧化碳(CO)、二氧化硫(SO2)、二氧化氮(NO2)等为主要环境污染物的城市空气污染问题越来越严重,环境空气质量预测日益受到政府及科研人员的重视,当前许多预测方法由于受到预测影响因素及预测方法本身的影响,使得预测数据与实际数据存在有较大的偏差。
早期的环境空气质量预测一般采用统计预测法[1],这种方法需要大量的实测数据和气象数据,且假定污染物源排放平衡且与浓度无关,这种方法存在明显的缺陷,现在大多采用空气污染数值预报法[2],此方法能给出定量的时空预测,但需要收集准确的污染源排放信息,难度较大,预测花费的时间较长,90年至今,更多的是运用更为科学完善的算法进行空气污染预测,如人工神经网络预测天气质量的方法[3],但城市环境空气质量受到污染源、地理环境、人口与交通密度以及风速、风向、温度、温度、气压、云量等因素的影响,环境空气质量预测至今还存在较多难以解决的问题。
人工神经网络具有较强的描述非线性映射和泛化能力,并能将多项空气预测因素如地理环境、气象、人类活动等特征充分利用,因此在当前环境空气质量预测中受到越来多的重视[4~5],但由于空气质量预测的困难性,单独采用一种算法进行空气质量预测具有明显的局限性,因此人工神经网络进行环境空气质量预测的效果并不理想,大多采用引入其他算法进行多种方法结合的方法进行预测,一些研究者已取得了一定的进步[6~8],近年来,随着群体智能算法[9~10]的快速发展,其中应用较为广泛的人工蜂群算法[11]也得到了快速发展,并在许多方面发挥了重要作用[12~13],本文以人工蜂群算法优化BP神经网络的方法进行环境空气预测。
2 反向传播神经网络学习原理
神经网络的学习过程实际就是整个神经网络的权值和阈值根据一定的算法不断调整以达到目标为止的过程,若干神经元整体的权值和阈值的不断调整,从宏观上来看,就呈现出一定的智能学习,神经网络学习的意义是通过大量权值和阈值的不断变化体现出来的,神经网络的学习算法大致有强化、无监督和有监督三大类,其中以有监督学习应用较为广泛,本文采用有监督神经网络学习算法以进行环境空气质量预测。
有监督学习神经网络的训练过程就是学习过程,设输入向量(输入信号)为 I(I1,…,Ii,…,Ip),输出向量为 O(O1,…,Oj,…,Ot),任意输入层节点 i与隐含层 j的权值(阈值)为Hij,隐含层节点 j到输出层节点K之间的权值(阈值)为 Ejk,若给定训练数据为 D={(I(i),T(i)},其中 I(i),T(i)是训练数据中第i个数据输入值和预期输出值,在神经网络的训练中通过参数的不断调整,其整个训练误差逐渐减少直至达到预定的条件为止,根据有监督学习神经网络原理,可以将学习过程中训练误差的变化过程以公式描述如下

其中N、Q分别表示神经网络训练数据中数据的个数及输出神经元的个数,训练好神经网络后,任意输入一组数据 I(N+1),就得到对应的预测数据O(IN+1|w)。
3 人工蜂群优化BP神经网络算法
人工蜂群算法是一种群体智能寻优算法,在多目标函数寻优中具有天然的优势,因其参数简单,有较高的寻优效率,在许多方面都有着广泛的应用,本文以人工蜂群算法优化神经网络的网络参数(权值和阈值),通过优化网络参数使得训练误差最小的权值问题,转化为若干组随机赋值的权值作为初始人工蜂群的种群进行群体智能寻优的问题,即以训练误差的倒数为适应度函数,适应度函数的最大值对应人工蜂群算法种群寻优所得的全局最优解,根据这个原理,在人工蜂群算法中初始时以随机化方式赋给每只蜜蜂的初始解即对应神经网络的一组初始权值,各只蜜蜂在飞行中寻找最优蜜源对应着神经网络根据梯度下降方式以训练误差的倒数作为适应度函数进行全局最优,虽然人工蜂群算法有着参数简单,效率较高,但在将其引入优化神经网络进行环境空气预测时,由于数据结构的复杂性,存在着明显的收敛慢且易陷入局部最优的问题,主要是人工蜂群算法中的三种蜜蜂即雇佣蜂、跟随蜂、侦察蜂都采用同一个寻优公式,但实际上这三种蜜蜂的寻优方式并不完全相同,因而本文将经典人工蜂群算法进行了改进,并将改进后的人工蜂群算法引入BP神经网络中,运用优化的BP神经网络进行环境空气质量预测。
3.1 对传统人工蜂群算法的改进
传统蜂群算法中蜜蜂搜索公式如下:

其中i,j,k,best∈[1,2,…,SZ],SZ表示算法中蜂群的规模,i≠k,FVi,j左边表示蜜蜂搜索前的位置,右边 FVi,j表示蜜蜂搜索后的位置,βi,j∈ [-1,1],是一个随机数,对于蜂群算法许多研究者进行了改进,其中比较典型的是GABC算法[14],其搜索公式如下
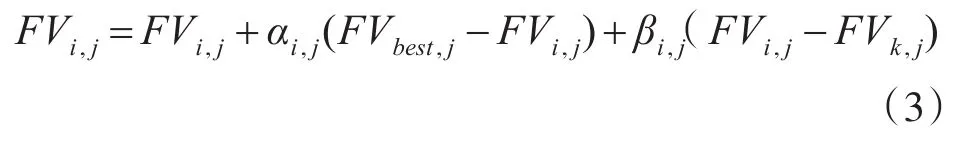
式(3)中,i,j,k,βi,j表示的意思同式(2),best∈[1,2,…,SZ],αi,j∈[0,1.5],FVbest,j表示当前全局最优位置的第j个元素,从GABC算法实验
结果来看,效果并不明显,主要原因是三种蜜蜂都采用了同一种搜索公式,为增加多样性,本文中将GABC算法作了改进,以式(2)作为侦察蜂搜索公式,以式(4)作为雇佣蜂搜索公式,式(4)如下

式(4)中右边第三项中 FVm,j的下标是从式(3)中的 FVi,j变化而来,由于 m 不同于 i,且 Ci,j∈[-2,2],因此增加了算法搜索的多样性。
由于跟随蜂是跟随雇佣蜂所寻蜜源附近进行寻优的,其搜索空间有一定的局限性,故对跟随蜂的搜索公式也进行了改进,通过增加莱维飞行因子,以增强其全局寻优能力,跟随蜂的搜索公式如式(5)所示:

式(5)在式(2)基础上增加了布谷鸟算法中的莱维飞行因素[15],FVl,j中 l是不同于 i,k的随机整数,式(5)中P服从标准正态分布,⊕表示点对点乘法,S为莱维搜索步长公式,其公式如下

其中u,v服从均匀分布。
式(5)中通过增加莱维因子将跟随蜂跟随雇佣蜂所寻找到的局部最优蜜源位置附近寻优的搜索空间进行了扩展,由于莱维因子的跳跃搜索有较大的搜索步长,因而增大了搜索空间的灵活性,提高了跟随蜂跳出局部最优的概率,并且式(5)中FVl,j中l的不同于i,k,也增加了搜索的多样性。
3.2 本文提出的蜂群优化神经网络算法
蜂群优化神经网络算法,可以克服BP神经网络学习过程中较多的“过拟合”现象,并加速BP神经网络的收敛速度,帮助BP神经网络脱离局部最优,其混合算法的整体思想是通过本文提出的改进人工蜂群算法,以训练误差的倒数作为适应度函数,因此要达到训练误差的最小只要寻找到适应度值最大的蜜蜂所寻找到的全局最优解即可,人工蜂群算法优化BP神经网络的算法如下:
初始化ABC算法,设蜂群规模为N,就是有N组不同的神经网络参数(权值或阈值),每一组参数的各个分量对应神经网络的各个权值或阈值。
定义人工蜂群算法中每只蜜蜂的适应度为对应神经网络的一组权值下误差值倒数,即根据式(1)和适应度的定义计算人工蜂群算法中三种蜜蜂的适应度值。
雇佣蜂按搜索公式在较大范围内寻优,若雇佣蜂获得局部最优解时,跟随蜂则在雇佣蜂所得局部最优位置继续寻优,侦察蜂则按自己的公式搜索寻优,并分别计算三种蜜蜂的寻优适应度值,并将蜂群算法中的蜜蜂以适应度值大小排序。
三种蜜蜂分别根据式(2)、(4)、(5)寻优,根据寻优的结果按照适应度值大小递减排序。
根据适应度值将三种蜜蜂重新分工,将适应度值较小的一组指派为侦察蜂,适应度值居中的一组指派为跟随蜂,适应度值较大的一组指派为雇佣蜂。
三种蜜蜂继续按式(2)、(4)、(5)寻优,不断迭代更新,当满足结条件时,算法结束,否则转式(3)。
输出算法所求得全局最优解,即为所求最优神经网络权值。
4 实验结果与分析
本改进神经网络空气浓度数据均采用日数据的形式输入,神经网络结构以三层MLP结构,其中输入层6个节点,其中浓度数据采用PM2.5、PM10、CO、NO2、SO2、O3六个指标数据,气象数据包括温度、湿度、气压、风向和风力五个指标,其中浓度数据的六个指标数据作为一个节点,每个浓度指标数据作为该节点的一部分,气象数据的五个指标作为五个节点,采用输出层一个节点,这个输出的浓度数据即是六维数据(包括PM2.5、PM10、CO、NO2、SO2、O3),隐含层15个节点,人工蜂群算法中种群规模为120。
本实验数据来自四川省达州市环保局官方发布的标准数据,并选取2016年10月和11月数据和2015年同期数据作为实验中训练和测试数据,预测数据采用当前污染物浓度和要预测未来时间的天气指标五个数据(温度、湿度、气压、风向和风力)来预测未来时间的污染物浓度数据,本实验通过传统BP神经网络、基于BP神经网络的人工蜂群算法(BP-ABC)、基于本文提出的改进人工蜂群BP神经网络算法(BP-IABC)三种算法作了比较实验,本实验计算机的配置为:主频为2.4GHz,内存4GB,环境为Windows7操作系统,在Matlab2014a平台中,选取了2016年12月预测数据和实际数据的实验结果,限于篇幅本文选取了实验中BP、BP-ABC、BP-IABC三种算法的SO2、PM10浓度值和预测值在2016年12月内31天的数据作了图示从具体数据上进行了详细比较其结果如图1及图2,并采用了均方误差即MSE,平均绝对误差百分比(MAPE),预测的平均准确率(PAC)三项评价性能指标从总体上作了比较,其结果如表1和表2,三项评价性能指标公式如(7~9),其均方误差即MSE公式如式(7)所示:

其中i=1,2,…,N表示实验中N个输入及输出数据,Ii和Oi分别表示实验中的第i个输入数据和输出数据。其平均绝对百分比误差以MAPE,其公式表示如式(8)所示:

环境空气污染物浓度数据的预测的平均准确率公式如式(9)所示:


图1 BP、BP-ABC、BP-IABC三种算法SO2浓度实际值和预测值比较图

图2 BP、BP-ABC、BP-IABC三种算法PM10浓度实际值和预测值比较图
图1、图2表示采用BP、BP-ABC、BP-IABC三种算法对四川省达州市2016年12月的环境空气污染物浓度数据预测数据和实际数据的详细比较,从图1和图2的数据来看,本文提出的BP-IABC算法的环境空气污染物浓度数据无论SO2还是PM10都是最接近实际数据,BP算法所得数据与实际数据偏离最大,BP-ABC所测数据与实际数据的误差比BP-IABC大比BP小。

表1 BP 、BP-ABC、BP-IABC三种算法SO2的MSE、MAPE、PAC指标结果比较

表2 BP、BP-ABC、BP-IABC三种算法PM10的MSE、MAPE、PAC指标结果比较
表1及表2是BP、BP-ABC、BP-IABC三种算法在四川省达州市2016年12月环境空气污染物浓度数据SO2、PM10的均方误差(MSE),平均绝对误差百分比(MAPE),预测的平均准确率(PAC)实验结果比较,从表1和表2可以看出,三种算法在两种污染物浓度数据的三项指标数据比较中,本文提出的BP-IABC算法MSE指标数据最小,平均绝对误差最小,而预测的平均准确率最高,说明本文提出的BP-IABC算法整体性能上要优于BP-ABC和BP算法,同样可以得出BP算法的预测性能在三种算法中性能是最差的。
5 结语
传统的BP神经网络进行环境空气质量预测时,由于传统BP神经网络本身固有的收敛速度慢、易陷于局部最优,很容易出现过拟合现象,导致网络模型训练时间过长,即使训练好的神经网络模型其环境空气质量预测的准确度也较低,本文在BP神经网络进行环境空气质量预测模型的训练过程中,通过对传统人工蜂群算法的改进,将改进的人工蜂群算法引入传统BP神经网络,用改进的人工蜂群算法优化传统BP神经网络权值和阈值,通过本文BP算法、BP-ABC算法、BP-IABC算法三种算法的环境空气质量预测的实验结果比较,实验结果表明本文提出的基于BP-IABC算法的环境空气质量预测模型性能最优,完全能应用于实际需要。
[1]陈世权,崔晓丹,黄严.空气污染预报方法简介[J].黑龙江环境通报,2005,29(1):47-48.CHEN Shiquan,CUI Xiaodan,HUANG Yan.Introduction to air pollution forecasting methods[J].Heilongjiang envi⁃ronmental bulletin,2005,29(1):47-48.
[2]雷孝恩,等.大气污染数值预报基础和模式[M].北京:中国气象出版社,1998:321.LEI Xiaoen,et al.Basis and model for numerical predic⁃tion of air pollution[M].Beijing:China Meteorological Press,1998:321.
[3]赵利刚.台州市环境空气质量与气象条件分析及神经网 络 预 报[J].安 徽 农 业 科 学 ,2009,37(18):8631-8633.ZHAO Feng.Analysis of Atmosphere Quality and Weather Condition and Expectation of Neural Network in Taizhou City[J].Journal of Anhui Agricultural Sciences,2009,37(18):8631-8633.
[4]吴有训,彭慕平,刘勇.基于径向基函数网络的宣城市空气质量预测[J].安徽师范大学学报(自然科学报)2011,34(4):374-379.WU Youxun,PENG Muping,LIU Yong.Prediction of air quality in Xuancheng based on radial basis function net⁃work[J].Journal of Anhwei Normal University(Natural Science Daily),2011,34(4):374-379.
[5]田静毅,范泽宣,孙丽华.基于BP神经网络的空气质量预 测 与 分 析[J].辽 宁 科 技 大 学 学 报 ,2015(2):131-136.TIAN Jingyi,FAN Zexuan,SUN Lihua.Prediction and analysis of air quality based on BP neural network[J].Journal of University of Science and Technology Liaoning,2015(2):131-136.
[6]赵宏,刘爱霞,王恺,等.环境空气S02和N02浓度的GA_ANN预测模型研究[J].计算机工程与应用,2010,46(8):199-201,213.ZHAO Hong,LIU Aixia,WANG Kai,et al.Research on GA_ANN prediction model of ambient air S02 and N02 concentration[J].computer engineering and applications,2010,46(8):199-201,213.
[7]李翔.基于GAB和模糊BP神经网络的空气质量预测[J].华中科技大学学报(自然科学版),2013,41:63-65.LI Xiang.Prediction of air quality based on GAB and fuzzy BP neural network[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2013,41:63-65.
[8]汪小寒,张燕平,赵姝,等.基于动态粒度小波神经网络的空气质量预测[J].计算机工程与应用,2013,49(6):221-224.WANG Xiaohan,ZHANG Yanping,ZHAO Shu,et al.Pre⁃diction of air quality based on dynamic particle size wave⁃let neural networks[J].computer engineering and applica⁃tions,2013,49(6):221-224.
[9]J.Kennedy,R.Eberhart,Particle swarm optimization.in:IEEE Int.Conf.Neural Networks,1995,1942-1948.
[10]Amer Draan,AmiraBouaziz,2014.Multilevel threshold⁃ing selection based on the artificial bee colony algorithm for image segmentation.Swarm and Evolutionary Compu⁃tation,16,69-84.
[11]D.Karaboga,An Idea Based on Honey Bee Swarm for Numerical Optimization[R].Kayseri:Erciyes Universi⁃ty,2005.
[12]D.-J.Liu,H.-J.Wang,S.Wang,G.-L.Pu,X.-Y.Deng,X.Hou,Quaternion-based improved artificial bee colony algorithm for color remote sensing image edge detection[J].Mathematical Problems in Engineering,2015,2015:138930.
[13]W.Y.Szeto and Yu Jiang.Hybrid Artificial Bee Colony Algorithm for Transit Network Design.Journal of the Transportation Research Board[J].Transportation Re⁃search Board of the National Academies,Washington,D.C.,2012:47-56.
[14]G.P.Zhu,S.Kwong,Gbest-guided artificial bee colony algorithm for numerical function optimization,Appl Math Computat 217(2010)3166-3173.
[15]Yang Xingshe,Deb S.Cuckoo Search via Levy Flights[C]//Proc.of World Congress on Nature&Biologically In⁃spired Computing.Coimbatore,India:[s.n.],2009.
