机器人柔性关节建模及零位标定研究∗

梅浩 刘永

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

机器人是一种高度集合化的技术装备，它将控制、材料、电子、传感器和机械等方向技术有效地集合于一体，从而让其具有了多方面的优点。为此，其相关的应用也是越来越广泛，但是现今的机器人重复定位精度高而绝对定位精度低，为了达到更多较高难度工作任务的需要，准确地标定出机器人参数就显得尤为重要［1］。

对于机器人标定，它就是采用测量手段或者基于运动学模型的参数识别方法辨识出机器人模型的准确参数，从而提高机器人绝对精度的过程［2］。其相关标定是由正标定和逆标定、自标定以及参数标定等重要标定技术［3］构成。其中，参数标定是获得运动学模型的一种相对有效且经济的标定方法［4～6］。零位标定作为参数标定中的一种，是提高机器人定位精度最重要的一种标定方法［7］。

机器人精度误差问题来自于多个方面，其中主要来源［8］是机器人的制造加工误差、关节零位误差等几何误差，利用常规的标定误差模型，能够较好地解决误差问题，而对于某些特定的机器人而言，其不仅含有几何误差，还含有一定由连杆和关节导致的柔性误差，这种综合性的误差成分促使常规误差建模的难度系数加大，而且很难辨识并补偿。

本文对机器人柔性关节建模及零位标定进行研究。分析机器人柔性关节的变形规律，建立柔性关节的误差模型，并分别考虑在末端负载和机械臂自重的影响下，相关误差模型的构建，结合工业机器人IRB120和实验环境特点，改进原来的零位标定误差模型，通过仿真和实验，对比原来误差模型和改进误差模型的标定效果。

2 柔性关节模型

2.1 柔性关节模型

由于机器人关节本身功能所需要，决定了关节整体结构需较为紧凑，所以在机械臂各关节中，大部分情况都是采用谐波齿轮减速器，而关节柔性产生的误差最主要原因就是谐波齿轮减速器。为了较好地掌握关节柔性变形，我们需要知道其变形规律，Spong［9］提出了机器人柔性关节的误差模型。

针对柔性关节的建模，Spong提出两点，其一，在模型中把关节的柔性描述成一个线性弹簧，其相应的比例系数就是关节的弹性系数；其二就是把电机的转子当作在转轴上一个整体。

通过Spong的假设，我们会发现，其是把具有n个自由度的柔性关节机器人模型用一个四阶动力学模型来表示：

式中，Jm、M(q)、K分别代表电机转动惯量矩阵、连杆转动惯量矩阵和关节的扭转刚度，qm、q分别代表电机角度向量和关节角度向量，C(q，q˙)、g(q)分别代表离心力与哥氏力项矩阵和重力向量。

在此模型中，我们可以得到关节柔性误差导致的关节偏转角表示［10］，具体如下

其中，δθC表示由于关节挠性形变导致的关节偏转角，单位为弧度；τ是施加在关节i轴线上的等效力矩；Cθ代表关节i的柔性系数。

因此，基于上式得到的关节偏转角将柔性误差转化成机器人末端位姿误差，具体如下

在该式中，我们用ΔXC表示机器人末端位姿误差，用JC表示柔性偏转角雅可比矩阵，用δθC表示由机器人各关节柔性偏转角构成的矢量。若只考虑空间坐标变化，则有

其中，ΔDC表示机器人末端位置误差，MC表示柔性偏转角的平移系数矩阵，Cθ表示柔性系数矩阵，τ表示等效力矩矢量。

2.2 自重柔性误差模型

IRB120机型中连杆2、3质量最大，机械臂自重施加在关节2和关节3上的力矩最大，因此自重主要影响关节2和3的柔性，其他关节的柔性相比很小，可将其忽略。

机械臂的几何结构如图1所示，G2和G3分别为连杆2和连杆3的重心，L1和L2分别为某姿态时，G2和G3到关节2和关节3的距离，L3为连杆2的长度，θ2和θ3为关节2、3的零位关节角值，偏转角θgiC的方向定义也是如此，C2和C3分别为关节2和关节3的柔性系数，关节2和关节3由于机械臂自重所受的力矩［11］分别如下

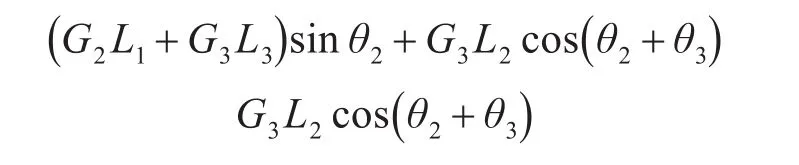
并将其代入上面的关节误差模型式（2），从而得到关节2和关节3由于机械臂自重转过的微小角度，分别如下

图1 机械臂几何简化结构

其中，在θgiC的下标中，g表示的是关节受到机器人自重导致关节产生误差，iC表示的是关节i的关节柔性系数C。令

则式（5～6）可以改写为

将其改写成矩阵相乘的形式即为

则式（12）可以用于表示关节2和关节3在受机械臂自重影响下的柔性误差模型。

2.3 外加负载柔性误差模型

关节2和关节3由于机械臂末端加载的负载所受的力矩分别如下

并将其代入上面的关节误差模型式（2），从而得到关节2和关节3由于负载转过的微小角度，如下

其中，在θliC的下标中，l表示的是关节受到机器人末端负载导致关节产生误差，iC表示的是关节i的关节柔性系数C。式中，L4为关节3到末端点的长度，Gl为机械臂末端所加负载的重力，令

则可以将式（13）和（14）分别转化为

将其转化成矩阵相乘的形式：

则式（20）可以用于表示关节2和关节3在受机械臂末端负载影响下的柔性误差模型。

3 零位标定模型

3.1 D-H模型

为了对机器人进行标定，首先要建立运动学模型，D-H模型［12］是应用最广泛的一种机器人建模模型，D-H模型可以唯一地描述机器人运动链的结构。D-H模型用 θi，di，ai，αi四个参数描述机器人每个杆件坐标系，模型中坐标系转换的T=R(θi)T(di)T(ai)R(αi)具体如下

其中，θi为关节角度，即为从 Xi-1轴绕Zi轴旋转到Xi轴的角度，绕Zi轴逆时针方向为正；αi为杆件扭角，即为从Zi-1轴绕 Xi轴到Zi轴的角度，绕 Xi轴逆时针方向为正；ai为杆件长度，即为从Zi-1轴沿着 Xi轴方向到Zi轴的距离，沿 Xi轴方向为正；di为关节长度，即为从 Xi-1轴沿着Zi轴到 Xi轴的长度，沿Zi轴的方向为正。

则六自由度机器人从基坐标系到末端坐标系的变换矩阵可得如下

将机器人每个关节角代入对应的齐次变换矩阵即可得到机器人末端的姿态与位置矩阵，简化计算结果如下

其中，(nx，ox，ax)，(ny，oy，ay)，(nz，oz，az)为机器人末端坐标系X、Y和Z轴上单位向量在机器人基坐标系上的坐标值，(px，py，pz)是机器人末端点在基坐标系下的坐标值。

3.2 零位标定误差模型

第i个关节的零位误差值用Δθi来表示，依据D-H模型，可以得到各个关节轴之间的变换矩阵，带入零位误差值到变换矩阵中，从而得到如下所示的齐次变换矩阵［13～14］：

3.3 改进的零位标定误差模型

对于原来的零位标定误差模型而言，如果每个关节的零位误差值Δθi是固定值，或随机械臂的准静态运动而变化很小，则基于原有误差模型的标定效果是非常好的，但当每个关节的θi误差值会随关节角状态的变化而有较大变化的时候，原来的标定方法会对参数误差出现难以辨识的问题，影响标定的效果。考虑到IRB120机型存在的误差因素不仅含有零位误差，还含有一定的关节柔性误差。根据前面对柔性误差的研究分析，可以将原来的标定误差模型进行改进，让改进后的误差模型考虑更多的误差因素，从而提升标定效果，其相应的误差模型具体如下

在该标定过程中，由于机械臂末端的负载很小，可以忽略不计，因此关节柔性仅受机型自重的影响。根据IRB120机型的特点，可知该机型关节柔性误差主要集中在关节2和关节3处，所以为实现更好的标定，在关节2和关节3处使用改进的误差模型，其他关节保持原来的误差模型，通过将两个误差模型结合使用以实现对该机型的零位标定。对于关节2和关节3其改进模型中的τi分别为

其中，G2为连杆2的重力，G3为连杆3和以上连杆总重力，L1为连杆2重心点和关节2轴中心的距离，L2为连杆3和以上连杆合体的重心点和关节3轴中心的距离，L3为连杆2的长度，θ2和θ3为关节2和关节3相对零位位姿的转角。

因此，不仅需要标定六个关节角的误差，还需要标定相应关节角的柔性系数误差。

4 仿真实验与结果分析

本文主要是针对机器人柔性关节建模及零位标定进行研究，实验平台是工业机器人IRB120。

在仿真含有零位误差、关节柔性误差和随机误差的综合影响下，我们对原来的误差模型和改进的误差模型进行对比仿真实验。在IRB120运动学参数标定仿真系统中，给该标定仿真系统添加误差：添加关节柔性误差，设定关节2和关节3的柔性系数分别为-5.921122e-05(N·m)-1、-9.137836e-06(N·m)-1；添加零位误差值，如（0，-1，-2，-1，1，-2）；添加随机误差，在每次进行让激光线打到位置敏感检测器（Position Sensitive Detector，PSD）中心点之前，向该机器人的D-H模型的第5个关节的杆件长度a5和关节长度d5添加随机的误差值，从而实现多次改变系统的随机误差值，对于系统的噪声如下

对于该随机误差源，其为（0，1）之间的随机数，通过多次重复添加，且每次添加不同的随机误差噪声。

以不同的姿态让机器人末端的激光线都交于一点［15～17］，采集420组关节角值，将其中的210组数据用原来的误差模型和改进的误差模型分别进行标定，利用剩余的210组数据进行标定效果的验证工作。由于每次零位标定仅需要7组数据，所以原先用于标定的210组数据可以对每个误差模型重复进行30次标定，将30次标定结果求取平均值即为平均标定结果。利用平均标定结果对210组关节角数据分别进行误差补偿，根据补偿后的关节角计算激光线在PSD感光面上的投影点，以及投影点与PSD中心点的距离值即距离误差，累加该误差值并求取平均值即得到平均距离误差，越小则说明标定的效果越好。

图2～3是分别用这两个模型进行仿真的结果。

利用原来误差模型和改进误差模型标定的结果进行测试数据的误差补偿，计算得到平均距离误差值分别为0.9692mm和0.5772mm，可见前者还残余较多的误差未能标定出来，说明改进误差模型标定的效果要更好。

从图2和图3可知，利用平均标定结果将用于验证标定效果的210组关节角数据分别进行误差补偿，根据补偿后的关节角计算激光线在PSD感光面上的投影点，其中（0，0）点为PSD中心点，点越接近（0，0）点，说明标定效果越好，通过两图中红点的分布可知，点更为聚集的改进误差模型具有更好的标定结果。

图2 验证原误差模型标定的效果

图3 验证改进误差模型标定的效果

本文实验基于ABB IRB120工业机器人，分别用原来的误差模型和改进的误差模型进行了相应的零位标定实验内容。在机械臂运动范围内的任意一个位置实现点约束，在每个位置进行7次定位并采集关节角数据，从而计算得到标定结果。选择5个不同的位置点重复进行实验，将5个位置点得到的标定结果求取平均值，具体结果如表1所示。

表1 原来的和改进的误差模型零位标定结果对比

为了验证两个误差模型在基于点约束的零位标定实验中哪个效果会更好，本文在机械臂工作空间内任意选择10处不同的位置分别实现点约束，将表1中两种不同误差模型得到的参数误差进行补偿，计算每个位置点所有直线两两交点或公垂线点的平均值点，然后求取每个位置点的平均值点和两直线交点或公垂线点的距离误差，将10个位置点所有的距离误差进行累加求取平均值，即为平均距离误差，并求取相应的误差方差值，平均距离误差值越小则说明标定效果越好。将原来的误差模型和改进的误差模型得到的平均距离误差值进行对比，对比结果如表2所示。

表2 原来的和改进的误差模型零位标定精度对比（mm）

从表2可以看出，相比较于未使用标定，改进前后的误差模型都能取得精度上的提升，但改进误差模型的标定效果比原来误差模型要更好，从而在绝对定位精度方面会有更大的提高。

5 结语

本文主要研究机器人柔性关节的建模，以及在关节柔性影响下的零位标定。分析了柔性关节的变形规律，建立了柔性关节的误差模型，并分别在末端负载和机械臂自重的影响下构建了相关具体模型。结合对柔性关节的研究，改进了原有的零位标定误差模型。在关节柔性误差、静态几何误差和随机误差的综合影响下，分别用原来误差模型和改进误差模型进行了零位标定的仿真实验，并基于工业机器人IRB120进行了实验验证。实验结果表明，不管在仿真情况下，还是在具体实验中，考虑了关节柔性的误差模型都能取得更好的标定效果，具有更好的误差模型完整性。下一步将研究该柔性关节模型是否对运动学参数标定的效果也具有一定的提升作用。

［1］龚星如，沈建新，田威，等.工业机器人的绝对定位误差模型及其补偿算法［J］.南京航空航天大学学报，2012，44（B04）：60-64.GONG Xingru，SHEN Jianxin，TIAN Wei，et al.Absolute Positioning Error Model of Industrial Robot and Compensa⁃tion Algorithm［J］.Journal of Nanjing University of Aero⁃nautics&Astronautics，2012，44（B04）：60-64.

［2］王东署.工业机器人标定技术研究［D］.沈阳：东北大学，2006.WANG Dongshu.Research on Calibration Technology of Industrial Robot［D］.Shenyang：Northeastern University，2006.

［3］王东署，迟健男.机器人运动学标定综述［J］.计算机应用研究，2007，24（9）：8-11.WANG Dongshu，CHI Jiannan.Survey on Robot Kinemat⁃ics Calibration［J］.Application Research of Computers，2007，24（9）：8-11.

［4］任永杰，邾继贵，杨学友，等.利用激光跟踪仪对机器人进行标定的方法［J］.机械工程学报，2007，43（9）：195-200.REN Yongjie，ZHU Jigui，YANG Xueyou，et al.Method of Robot Calibration Based on Laser Tracker［J］.Chinese Journal of Mechanical Engineering，2007，43（9）：195-200.

［5］李定坤，叶声华，任永杰，等.机器人定位精度标定技术的研究［J］.计量学报，2007，28（3）：224-227.LI Dingkun，YE Shenghua，REN Yongjie，et al.Research on Robot's Positioning Accuracy Calibration［J］.Acta Met⁃rologica Sinica，2007，28（3）：224-227.

［6］叶声华，王一，任永杰，等.基于激光跟踪仪的机器人运动学参数标定方法［J］.天津大学学报，2007，40（2）：202-205.YE Shenghua，WANG Yi，REN Yongjie，et al.Calibration of Robot Kinematic Parameters Based on Laser Tracker［J］.Journal of Tianjin University，2007，40（2）：202-205.

［7］Chen H，Fuhlbrigge T，Sang C，et al.Practical industrial robot zero offset calibration［C］//IEEE International Con⁃ference on Automation Science and Engineering，2008：516-521.

［8］焦国太，冯永和，王锋，等.多因素影响下的机器人综合位姿误差分析方法［J］.应用基础与工程科学学报，2004，12（4）：435-442.JIAO Guotai，FENG Yonghe，WANG Feng，et al.Syntheti⁃cally Analysis of the Robot Pose Error Resulting from Vari⁃ous Factors［J］.Journal of Basic Science and Engineering，2004，12（4）：435-442.

［9］Spong M W.Modeling and Control of Elastic Joint Robots［J］.Asme Journal of Dyn.sys.meas.&Cont，1987，109（4）：310-319.

［10］Gong C，Yuan J，Ni J.Nongeometric error identification and compensation for robotic system by inverse calibra⁃tion［J］.International Journal of Machine Tools&Manu⁃facture，2000，40（14）：2119-2137.

［11］王一，刘常杰，任永杰，等.工业坐标测量机器人定位误差补偿技术［J］.机械工程学报，2011，47（15）：31-36.WANG Yi，LIU Changjie，Ren Yongjie，et al.Compen⁃sation for Positioning Error of Industrial Coordinate Mea⁃surement Robot［J］.Journal of Mechanical Engineering，2011，47（15）：31-36.

［12］Gao B，Liu Y，Xi N，et al.Developing an Efficient Cali⁃bration System for Joint Offset of Industrial Robots［J］.Journal of Applied Mathematics，2014，2014：1-9.

［13］Liu Y，Xi N，Zhao J，et al.Development and sensitivity analysis of a portable calibration system for joint offset of industrial robot［C］//IEEE/RSJ International Conference on Intelligent Robots and Systems，2009：3838-3843.

［14］Liu Y，Xi N，Zhang G，et al.An automated method to calibrate industrialrobotjointoffsetusing virtual line-based single-point constraint approach［C］//IEEE/RSJ International Conference on Intelligent Robots and Systems，2009：715-720.

［15］Liu Y，Shen Y，Xi N，et al.Rapid robot/workcell cali⁃bration using line-based approach［C］//IEEE Interna⁃tional Conference on Automation Science and Engineer⁃ing，2008：510-515.

［16］Shen Y，Xi N，Li X，et al.Robot localization using an uncalibrated PSD servoing approach［C］//IEEE 7th World Congress on Intelligent Control and Automation，2008：535-540.

［17］Liu Y，Xi N，Shen Y，et al.High-accuracy visual/PSD hybrid servoing of robotic manipulator［C］//IEEE/ASME International Conference on Advanced Intelligent Mecha⁃tronics，2008：217-222.