中心区企业生产率优势的来源:集聚、选择抑或分类效应
2018-04-24王良举王永培袁平红
王良举 王永培 袁平红
(1.安徽财经大学 工商管理学院,安徽 蚌埠 233030; 2.南京审计大学 经济学院,江苏 南京 211815;3.安徽财经大学 国际经济贸易学院,安徽 蚌埠 233030)
一、引言
城市经济学以及经济地理学研究表明,位于经济活动密集的中心区(大城市)的企业通常比外围地区(小城市)的企业拥有更高的生产率(Ciccone et al.,1996;Melo et al.,2009;Puga,2010;范剑勇,2006)。而关于中心区企业生产率优势来源的讨论,主要存在三种观点。第一种观点是,经济活动集聚会通过技术溢出、劳动力市场蓄水池效应以及更加靠近供应商与消费者带来正的外部性(即集聚效应),使得中心区企业拥有更高的生产率(Fujita et al.,2002;Marshall,1920)。第二种观点是,低效率企业因为无法应对中心区激烈的竞争而退出,唯有高效率企业能够在中心区生存下去,导致中心区企业拥有更高的平均生产率,即所谓的选择效应(Baldwin et al.,2006;Behrens et al.,2014)。Baldwin et al.(2006)将异质性企业模型(Helpman et al.,2004;Melitz,2003;Melitz et al.,2008)与自由资本模型(Martin et al.,1995)相结合分析了异质性企业选址行为,证明分类效应也是中心区企业生产率优势的重要来源。中心区意味着更大的市场规模和激烈的市场竞争,高效率企业在中心区选址能获得更大的市场份额,同时也能应对更加激烈的市场竞争,因而高效率企业倾向于在中心区选址,而低效率企业则倾向于分布在外围地区(Baldwin et al.,2006;Forslid et al.,2014;Okubo et al.,2010)。
中心区企业生产率优势究竟是来源于正的集聚外部性,还是因为中心区低效率企业被淘汰,抑或是因为高效率企业主动在中心区选址?厘清这一问题,对于制定区域和城市发展政策以及评估相关政策的实施效果,具有重要的现实指导意义。
二、文献综述
异质性企业非随机的区位选择带来的选择效应与分类效应会对地区生产率差异带来内生性影响,导致基于新经济地理理论测度集聚效应的标准实证技术可能高估了集聚效应的作用(Baldwin et al.,2006;Combes et al.,2011;Ottaviano,2011)。如何准确识别集聚效应、选择效应与分类效应对地区生产率差异的影响,已成为融入异质性企业理论的新新经济地理学探讨的重要议题。
Syverson(2004,2007)针对美国混凝土行业的研究发现,由于存在选择效应,中心区企业比外围地区的企业拥有更高的效率。Saito et al.(2009)基于智利食品行业企业数据的研究发现,集聚效应和选择效应均存在,但选择效应的作用更显著。Combes et al.(2012)采用法国制造业企业数据,开创性地通过考察不同地区企业生产率分布截尾上的差异来识别集聚效应与选择效应,研究发现地区生产率差异基本可以由集聚效应来解释,但是在一些相对分散的部门中选择效应也是地区生产率差异的重要来源。李晓萍等(2015)运用Combes et al.(2012)的方法,采用中国地级市工业企业数据检验了集聚对企业生产率的影响以及异质性企业选择效应的存在性及其程度。结果发现,集聚效应与选择效应均是地区企业生产率差距产生的重要原因,但集聚效应的作用更显著。王永进等(2016)同样运用Combes et al.(2012)的方法,对开发区和非开发区的生产率分布进行了比较,识别了开发区的“集聚效应”和“选择效应”。研究发现,“集聚效应”和“选择效应”都显著提高了开发区的生产率水平。余壮雄等(2014)基于格点搜索的回归方法识别集聚效应与选择效应,研究表明集聚效应是导致中国大城市生产率优势的重要原因,而选择效应并不存在。刘海洋等(2015)运用分位数方法探讨了中国企业生产率的地域分布特征,发现中国集群地区的生产率优势源于选择效应而不是集聚效应。
需要指出的是,上述各项研究所讨论的选择效应中实际上均包含了分类效应。尽管集聚效应、选择效应与分类效应在宏观上最终均表现为企业生产率的提高,但产生这一结果的微观机制并不相同。集聚效应是通过共享、匹配和学习三种微观机制带来的正的集聚外部性提升了本地区所有企业的生产率;选择效应的作用机制则是通过淘汰低效率企业使企业平均生产率得以提升的;而分类效应的作用机制是通过企业的区位选择,即高效率企业在中心区选址,低效率企业在外围地区选址,使中心区企业拥有更高的生产率。此外,上述三种效应之间还可能会产生相互作用(Behrens et al.,2014)。中心区的市场规模更大,同时市场竞争也更加激烈,也就是说选择效应更强,在优胜劣汰的自然法则下只有高效率企业才会选择在中心区选址,低效率企业则分布在外围地区,即选择效应引致分类效应;而更多高效率企业在中心区选址进一步加剧了中心区市场竞争的激烈程度,即分类效应会进一步强化选择效应。但迄今为止,仅有少量研究将选择效应与分类效应区别开来加以讨论。Behrens et al.(2014)通过构建城市系统模型,将集聚效应、选择效应与分类效应纳入统一的理论框架,阐释了大城市生产率优势的来源,并基于美国276个大都市统计区数据进行实证检验,研究发现美国大城市的生产率优势主要来源于集聚效应和分类效应,但选择效应并不显著。Forslid et al.(2014)在空间分类模型(Baldwin et al.,2006)中引入企业(部门)资本强度差异,采用日本制造业企业数据的研究发现,高资本强度行业中存在双边分类效应(two-sided sorting),即高效率企业和低效率企业均在中心区选址,而中等效率企业分布在外围地区。陈强远等(2016)基于双城模型构建大城市企业生产率溢价概念框架,对中国大城市企业生产率溢价的来源进行了考察。该文是目前为止对中国大城市企业生产率优势来源最全面的微观层面的讨论。需要指出的是,该文讨论的竞争效应是指高效率企业能够从集聚经济中获益更多,表现为企业生产率密度分布的扩张(Combes et al.,2012),本质上是集聚效应的重要构成部分。
理论层面的文献对中心区企业生产率优势的来源以及上述三种效应的存在性进行了较为深入的讨论,但很少有文献从实证层面将三种效应同时加以考察。当前,新新经济地理方面的研究在中国仍处于起步阶段,相关的理论研究和实证检验十分缺乏。本文借鉴Forslid et al.(2014)的实证思路,采用中国制造业企业微观数据,使用半参数方法测算企业全要素生产率,在此基础上使用分位数方法识别集聚效应、选择效应与分类效应的存在性,从企业异质性视角为中心区生产率优势的来源以及中国地区生产率差异提供一种新的微观解释。
三、企业全要素生产率测算
(一)测算方法
采用Syverson(2011)的方法,假设企业生产函数为标准的柯布—道格拉斯生产函数:
(1)
其中,Yit、Kit和Lit分别表示企业i在t时期的产出、资本投入和劳动投入,βK、βL分别表示资本和劳动的产出弹性,Ait为企业i在时期t的全要素生产率(Total Factor Productivity,TFP)。对式(1)两边取自然对数可以得到如下线性形式:
yit=βKkit+βLlit+uit
(2)
式(2)中,yit、kit和lit分别表示Yit、Kit和Lit的对数形式,残差项uit包含了对数形式的企业全要素生产率信息。常用的做法是通过估计式(2)得到资本和劳动的产出弹性进而估算企业全要素生产率。
实际生产中,企业通常会根据自身前期的生产率调整本期的要素投入组合,且生产率冲击和企业退出市场的概率存在一定的相关性,如果直接使用最小二乘(OLS)或固定效应(FE)方法估计式(2)可能会导致严重的内生性问题,造成测算的企业全要素生产率存在较大偏误。为了克服传统方法难以避免的由联立性偏误和选择性偏误带来的内生性问题,Olley et al.(1996)发展了基于一致半参数的估计方法(简称OP方法),采用三阶段模型估计企业全要素生产率。OP方法用企业当期投资作为不可观测的生产率冲击的代理变量,解决联立性偏误问题;此外,OP方法将企业退出行为纳入分析框架,通过生存概率估计企业进入和退出,从而克服样本选择性偏误。OP方法假定代理变量(企业当期投资)与企业产出保持严格单调关系,这意味着投资为零的企业样本都会被剔除。但实际中,并非所有企业在各期投资均大于零,如果使用OP方法会使得很多企业样本在估计中被丢弃。Levinsohn et al.(2003)针对这一问题发展了一种新的半参数估计方法(简称LP方法)。LP方法采用数据更易获得的中间品投入取代企业当期投资作为不可观测的生产率冲击的代理变量。本文采用LP方法估计中国制造业企业资本及劳动要素的产出弹性的一致估计量,进而测算中国制造业企业的全要素生产率。
产出Yit用企业工业增加值来表示,并用企业所在省份工业品出厂价格指数进行平减;资本投入Kit用企业固定资产净值年均余额表示,并用企业所在省份固定资产投资价格指数进行平减;劳动投入Lit用企业全部从业人员年平均数表示;中间品投入mit用企业中间投入表示,并用企业所在省份的原材料、燃料和动力购进价格指数进行平减。各省份工业品出厂价格指数、固定资产投资价格指数以及原材料、燃料和动力购进价格指数来源于相应年份的《中国统计年鉴》,各类价格指数均以2000年为基期。
(二)数据处理
本文使用的微观企业层面的基础数据来源于中国工业企业数据库,样本期间涵盖2001—2007年。该数据库是基于国家统计局开展的“规模以上工业统计报表统计”取得的统计资料整理而成的。统计对象包括全部国有和规模以上非国有工业法人企业。统计口径包括“采掘业”、“制造业”以及“电力、燃气及水的生产和供应业”三大门类,其中制造业占90%以上。该数据库提供了相当数量的微观企业的详细信息,一类是企业经营成果有关的信息,包括资金流量表、资产负债表和损益表的主要信息以及雇用员工和生产活动信息;另一类是对企业身份、生产经营活动内容和状态进行定性描述的信息。近年来,该数据库在经济研究领域得到了广泛应用,产生了一系列针对中国问题的高质量研究成果,并形成了大量具有较强实际指导意义的政策建议。但是该数据库也存在样本匹配混乱、指标缺失以及统计口径误差等问题,给研究人员使用带来了较大困难。本文参考聂辉华等(2012)的做法对该数据库进行了调整。具体包括:剔除企业总产值为负数或者全部从业人员年平均人数、中间投入合计、固定资产原价以及固定资产净值年平均余额等各项投入为负数的样本记录;剔除企业固定资产原值小于固定资产净值、企业工业增加值或工业中间投入大于总产出的样本记录;剔除从业人员年平均人数少于8人或主营业务收入低于500万元的企业样本;为保持行业统计口径前后一致,根据《国民经济行业分类与代码(GB/T4754—2002)》将2001年和2002年的企业样本按照细分行业进行调整。城市市辖区作为基础设施较为完善、人口和经济活动分布集中的连续区域,有利于集聚经济的形成。而且城市功能集中体现在市辖区,市辖区的基本情况大致反映了城市(狭义)各个主要方面。本文主要研究与经济活动集聚相关的集聚效应、选择效应与分类效应的存在性,因此选择地级以上城市市辖区作为空间单位进行考察更符合本文研究要求*如果未加特殊说明,本文使用的有关城市特征的数据(例如国内生产总值、城市土地面积等),其统计范围均是城市市辖区。。根据企业所在地区的行政区划代码进行筛选,保留位于城市市辖区的企业样本记录共计881542条。
采掘业以及制造业中的烟草制品业的空间分布很大程度上受制于煤炭、石油等自然资源的分布情况,自然资源在这些行业的企业生产中起到决定性作用;另外,电力、燃气及水的生产和供应业是典型的公用事业部门,其生产经营活动具有较强的公共属性。这些行业的生产函数不能简单假设为C-D生产函数,本文采用的LP方法不适用于分析这些行业的企业全要素生产率。因此,本文仅对29个制造业细分行业(两位数代码13—15、17—37、39—43)企业样本进行讨论。不同的企业面临的约束条件及采用的生产技术不尽相同,统一的生产函数难以准确地刻画所有企业的实际生产行为。为了尽可能真实地反映企业的技术水平,本文采用杨汝岱(2015)的做法,假定同一行业中的企业采用相似的生产模式,基于制造业两位数代码细分行业分类,采用LP方法分行业估计资本和劳动要素的产出弹性,在此基础上测算企业全要素生产率。
四、中心区企业生产率优势来源的实证检验
(一)中心区企业生产率优势的初步统计分析


图1城市市场潜能与企业全要素生产率关系
为了直观展现城市市场潜能与企业全要素生产率之间的关系,本文绘制了城市市场潜能(对数形式,ln mp)与企业全要素生产率均值(TFP_city)关系散点图。图1显示,城市市场潜能与企业全要素生产率呈正相关,也就是说位于市场潜能更大的中心区的企业具有一定的生产率优势。企业全要素生产率基本描述统计结果(表1)显示,中心区企业全要素生产率均值(6.801)大于外围地区企业全要素生产率均值(6.734)。从细分行业看,除皮革、毛皮、羽毛(绒)及其制品业(19),石油加工、炼焦及核燃料加工业(25)、化学纤维制造业(28),黑色金属冶炼及压延加工业(32)等4个两位数代码细分行业外,中心区其他25个两位数代码细分行业的企业全要素生产率均值高于外围地区,进一步说明位于中心区的企业具有较为明显的生产率优势。
(二)集聚效应、选址效应与分类效应的图形识别
城市市场潜能与企业全要素生产率关系散点图显示,中心区企业确实具有一定的生产率优势。但是我们并不清楚中心区企业生产率优势的具体来源。集聚效应、选择效应与分类效应可能共同引致中心区企业拥有更高的生产率,但是它们对企业生产率分布曲线的影响并不相同(Forslid et al.,2014)。如果仅存在集聚效应,中心区所有企业均能从集聚中获益,企业生产率分布曲线会整体右移;如果仅存在选择效应,中心区低效率企业因为激烈的竞争而退出,低效率企业的缺失将导致中心区企业生产率分布呈现“左断尾”,中心区企业生产率分布曲线的峰度会提高;如果仅存在分类效应,高效率企业和低效率企业分别在中心区和外围地区选址,外围地区高效率企业也会向中心区迁移,使得中心区企业生产率分布扩张而外围地区企业生产率分布呈现“右断尾”,中心区企业生产率分布曲线的峰度会降低。
这里,我们采用核密度估计企业生产率曲线,从总体上对中心区企业生产率优势的来源进行图形识别。核密度估计是用来估计未知的概率密度函数的非参数方法。这一方法不对模型的具体分布作任何假定,因而估计结果更加稳健。假设要估计连续型随机变量x在x0处的概率密度f(x0),那么其核密度估计量为:
(3)

从图2可以发现,总体来看,中心区企业生产率核密度曲线相对外围地区略微右移,说明存在集聚效应,经济活动在中心区集聚带来的正的外部性使得中心区所有企业均能从中获益;在核密度曲线左端,中心区企业生产率分布存在断尾现象,表明中心区存在更强的选择效应,低效率企业难以应对中心区激烈的市场竞争而退出,使得中心区低效率企业较少;而在核密度曲线右端,仅2001年和2002年中心区企业生产率核密度曲线略微前伸,其他年份中心区企业生产率核密度曲线与外围地区企业生产率核密度曲线几乎重叠,初步表明中心区并不存在显著的分类效应。

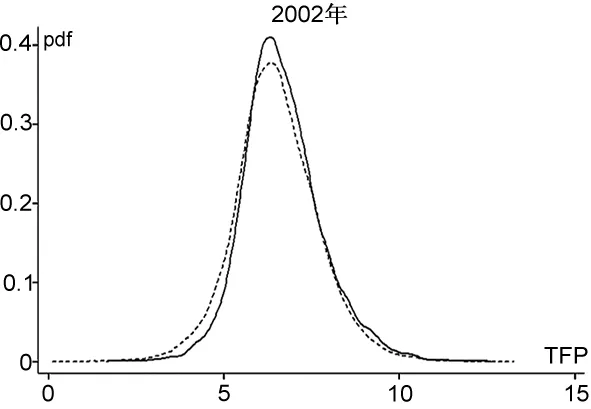

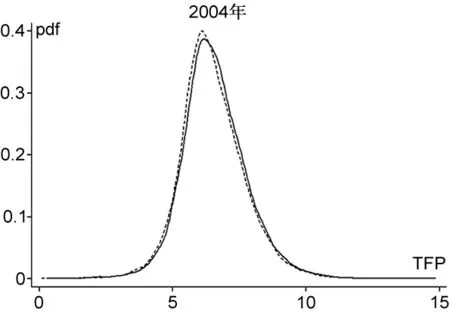

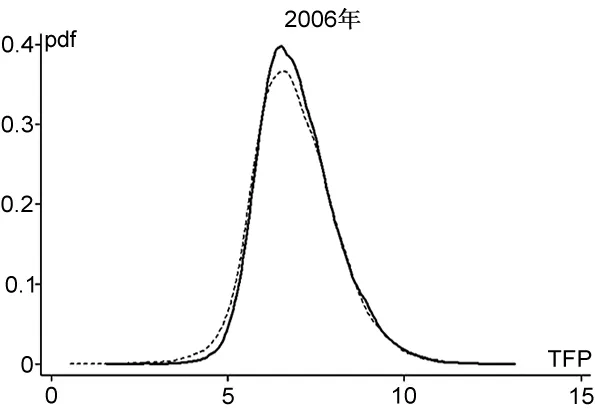
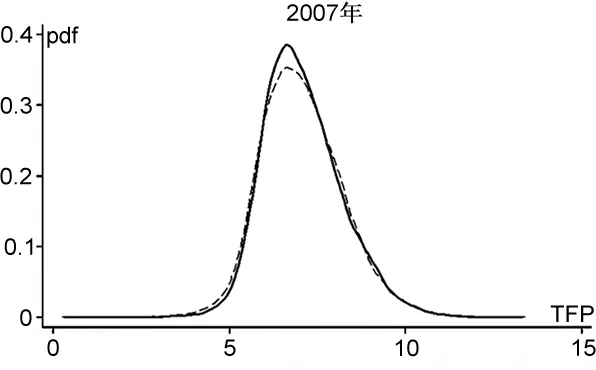
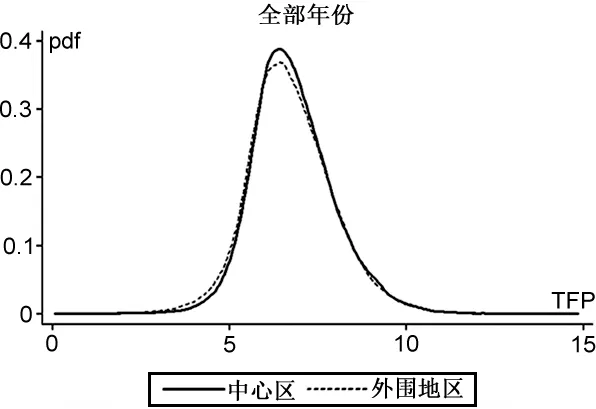
图2中心区与外围地区企业生产率核密度曲线
(三)集聚效应、选择效应与分类效应的分位数识别
图形识别虽然较为直观,但是难以准确刻画企业生产率密度函数的细微变化。这里,我们采用Syverson(2004)以及Forslid et al.(2014)等发展的分位数方法识别三种效应的存在性。如果存在集聚效应,中心区企业生产率分布不同分位数上的企业生产率均会提高;如果存在选择效应,中心区低效率企业较少,低端分位数上的企业生产率提高,四分位距(IQR)和离散程度变小;而如果存在分类效应,更多的高效率企业入驻中心区,中心区企业生产率分布曲线向前端扩展,高端分位数上的企业生产率提高,四分位距和离散程度变大。
从表1可以看出,多数情形下中心区企业生产率均值以及不同分位数上的企业生产率均大于外围地区,表明中心区存在显著的集聚效应;低端分位数上中心区企业生产率高于外围地区,而中心区企业生产率的四分位距和标准差小于外围地区,表明中心区存在显著的选择效应。就农副食品加工业(13),食品制造业(14),饮料制造业(15),非金属矿物制品业(31),仪器仪表及文化、办公用机械制造业(41),工艺品及其他制造业(42)等6个细分行业而言,中心区企业生产率均值、四分位距、标准差均大于外围地区,高端分位数上中心区企业生产率大于外围地区,意味着高效率企业在中心区选址且外围地区的高效率企业会向中心区迁移,表明中心区存在分类效应。就皮革、毛皮、羽毛(绒)及其制品业(19),石油加工、炼焦及核燃料加工业(25)、化学纤维制造业(28),黑色金属冶炼及压延加工业(32)等4个细分行业来看,中心区企业生产率均值以及不同分位数上的企业生产率均小于外围地区,表明集聚并没有带来生产率优势。进一步分析可知,上述4个细分行业的企业生产对空间分布分散且运输成本较高的矿产等原材料的依赖较大,中心区的拥挤效应(负的集聚外部性)使得企业并不能从集聚中获得显著的生产率优势。
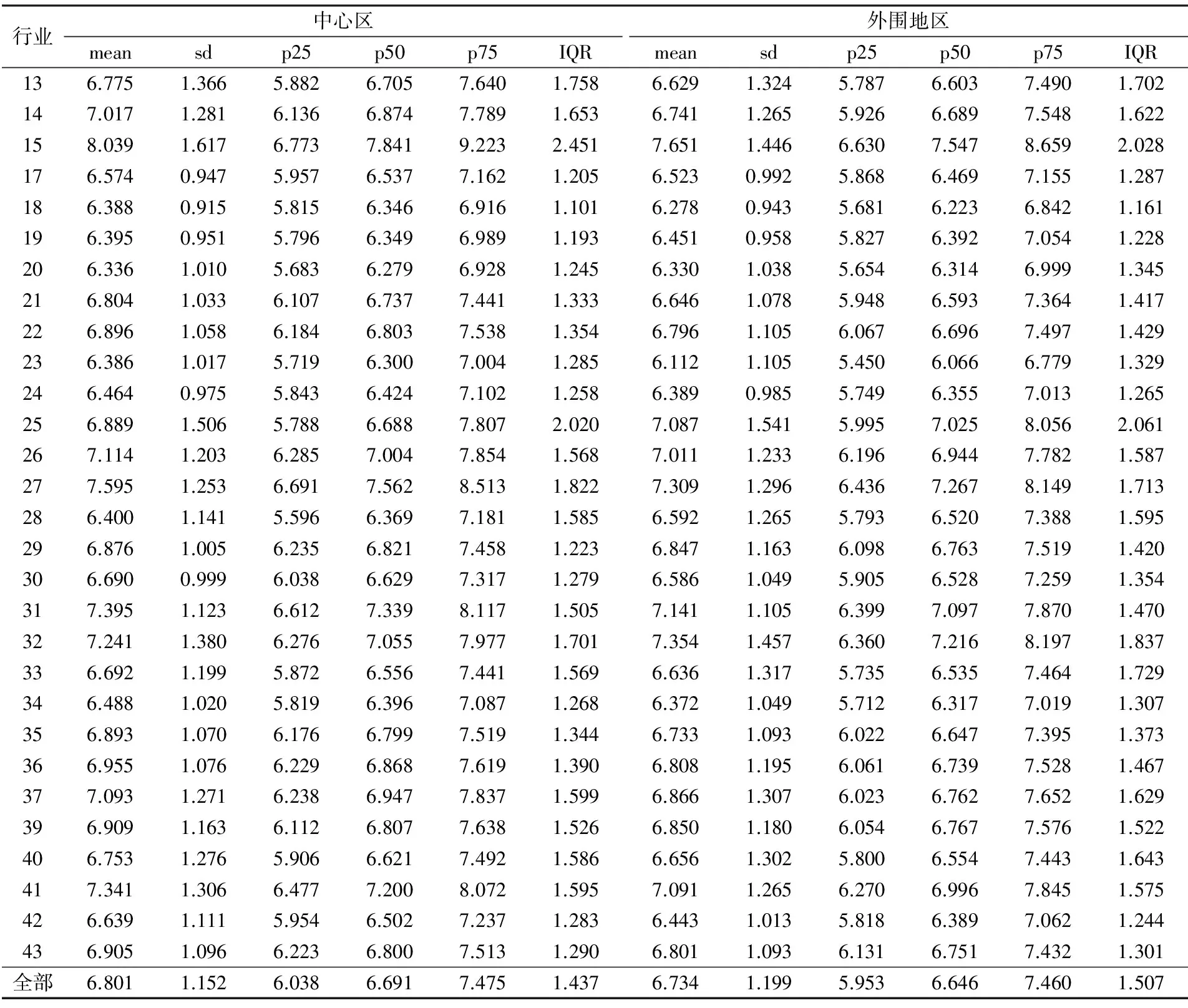
表1 企业全要素生产率描述统计结果
注:行业对照如下:13-农副食品加工业;14-食品制造业;15-饮料制造业;17-纺织业;18-纺织服装、鞋、帽制造业;19-皮革、毛皮、羽毛(绒)及其制品业;20-木材加工及木、竹、藤、棕、草制品业;21-家具制造业;22-造纸及纸制品业;23-印刷业和记录媒介的复制;24-文教体育用品制造业;25-石油加工、炼焦及核燃料加工业;26-化学原料及化学制品制造业;27-医药制造业;28-化学纤维制造业;29-橡胶制品业;30-塑料制品业;31-非金属矿物制品业;32-黑色金属冶炼及压延加工业;33-有色金属冶炼及压延加工业;34-金属制品业;35-通用设备制造业;36-专用设备制造业;37-交通运输设备制造业;39-电气机械及器材制造业;40-通信设备、计算机及其他电子设备制造业;41-仪器仪表及文化、办公用机械制造业;42-工艺品及其他制造业;43-废弃资源和废旧材料回收加工业。
值得注意的是,集聚效应、选择效应与分类效应可能会同时存在且相互作用,所以通过考察企业生产率分布的描述统计特征进而识别上述三种效应的存在性可能产生较大误差。因此,上述识别结果只是初步的。借鉴Forslid et al.(2014)的做法,将企业全要素生产率减去城市企业全要素生产率均值,过滤纯粹的集聚效应,重点关注选择效应与分类效应。本文采用分位数回归方法,对去均值的企业全要素生产率(TFP_demean)作关于中心区虚拟变量(Dummy_core)的回归,进行进一步细致分析。例如对第5百分位数的回归方程为:
P(xi (4) 如果低端百分位数上β估计值为正数,而高端百分位数上β估计值显著为负数,即中心区企业生产率分布两端肥尾,表明存在分类效应;如果低端百分位数上β估计值为负数,即中心区企业生产率分布左端截断,表明存在选择效应。特别地,如果低端百分位数上β显著为正,而高端百分位数上β显著为负,则表明存在双边分类效应。 本文采用bootstrap方法(自助法)估计参数标准误,表2给出了分位数回归的结果。从中可以看出,在第5百分位数上有2个细分行业β估计值为负,在第10百分位数上有6个细分行业β估计值为负,而在四分之一分位数上有9个细分行业β估计值为负,表明就部分细分行业而言,中心区的确存在更强的选择效应。在高端百分位数上,有相当数量的细分行业β估计值为负,表明中心区存在显著的分类效应。进一步分析发现,橡胶制品业(29)、塑料制品业(30)以及有色金属冶炼及压延加工业(33)等3个细分行业中,低端分位数上β估计值显著为正,而高端分位数上β估计值显著为负,表明存在双边分类效应,即高效率企业和低效率企业均在中心区选址,而中等效率企业在外围地区选址。上述结论进一步证实,除了集聚效应之外,选择效应与分类效应也是中心区企业生产率优势的重要来源。 表2 分位数回归结果 注:行业代码说明同表1;除了少数百分位数上由于样本企业过少导致β估计值不显著之外,绝大多数β估计值均非常显著,为了简洁,表中没有标注β估计值的标准误及显著性水平。 本文基于中国制造业企业微观数据,采用企业所在城市市场潜能的第75分位数划分中心区与外围地区,使用半参数方法测算了企业全要素生产率,在此基础上使用分位数方法识别中心区企业生产率优势的来源,揭示了经济集聚对企业生产率的影响以及异质性企业非随机的区位选择带来的选择效应与分类效应对企业生产率的影响,得出以下主要结论与启示: (1)中心区企业生产率优势可能是集聚效应、选择效应与分类效应共同作用的结果。集聚效应是中心区企业生产率优势的重要来源;但是在部分行业中,集聚效应与选择效应、分类效应共同作用导致中心区企业拥有明显的生产率优势。这说明中心区企业生产率优势可能是高效率企业主动在中心区选址或低效率企业迫于竞争压力而从中心区退出导致的,也就是说已有研究实际上高估了集聚效应的作用。可见,从企业异质性视角重新审视中心区企业生产率优势的来源,对于新型城镇化背景下中国城市发展道路的选择具有重要的政策含义。由于选择效应与分类效应的存在,通过补贴或税收优惠等促进外围地区发展的政策措施可能导致更多的低效率企业在外围地区选址,进一步扩大地区生产率差距。 (2)经济活动在中心区集聚带来的正的外部性使得中心区大多数行业的企业生产率得到提升,但是就皮革、毛皮、羽毛(绒)及其制品业,石油加工、炼焦及核燃料加工业、化学纤维制造业,黑色金属冶炼及压延加工业等4个细分行业而言,集聚并没有带来显著的生产率优势。这要求我们必须充分考量各地区吸引外来投资的“竞次式”补贴竞争(陶然 等,2009)可能带来的后果。“竞次式”补贴竞争虽然能够提升地区经济集聚水平,但也可能导致过度集聚进而对地区生产率产生不利影响。因此,各地区在制定促进经济集聚的政策措施的过程中,应该审慎思考相关政策措施实施后可能造成的过度集聚以及拥挤效应等负面影响。 (3)在橡胶制品业、塑料制品业以及有色金属冶炼及压延加工业等3个细分行业中,发现了双边分类效应存在的证据。这些行业内高效率企业和低效率企业均在中心区选址,唯有中等效率企业在外围地区选址。这说明以往基于新经济地理理论提出的吸引高效率企业在外围地区选址的补贴或税收优惠等政策措施可能难以实现预期的目标。 由于现有的新新经济地理分析框架的限制,本文未能对中心区企业生产率优势三大来源各自的重要性进行分解。如果能够厘清集聚效应、选择效应与分类效应对中心区企业生产率优势的贡献份额,那么可以更加全面、深刻地理解中心区企业生产率优势的具体来源。未来的研究如果能在这一领域取得突破,则可以为中国新型城镇化以及区域协调发展提出更具现实指导意义的政策建议。 参考文献: 陈强远,钱学锋,李敬子. 2016. 中国大城市的企业生产率溢价之谜[J]. 经济研究(3):110-122. 范剑勇. 2006. 产业集聚与地区间劳动生产率差异[J]. 经济研究(11):72-81. 李晓萍,李平,吕大国,等. 2015. 经济集聚、选择效应与企业生产率[J]. 管理世界(4):25-37. 刘海洋,刘玉海,袁鹏. 2015. 集群地区生产率优势的来源识别:集聚效应抑或选择效应[J]. 经济学(季刊)(3):1073-1092. 聂辉华,江艇,杨汝岱. 2012. 中国工业企业数据库的使用现状和潜在问题[J]. 世界经济(5):142-158. 陶然,陆曦,苏福兵,等. 2009. 地区竞争格局演变下的中国转轨:财政激励和发展模式反思[J]. 经济研究(7):21-33. 王良举. 2012. 空间交易成本、市场获得与企业区位[J]. 南大商学评论(2):1-25. 王永进,张国峰. 2016. 开发区生产率优势的来源:集聚效应还是选择效应[J]. 经济研究(7):58-71. 杨汝岱. 2015. 中国制造业企业全要素生产率研究[J]. 经济研究(2):61-74. 余壮雄,杨扬. 2014. 大城市的生产率优势:集聚与选择[J]. 世界经济(10):31-51. 周浩,余壮雄,杨铮. 2015. 可达性、集聚和新建企业选址:来自中国制造业的微观证据[J]. 经济学(季刊)(4):1393-1416. BALDWIN R E, OKUBO T. 2006. Heterogeneous firms, agglomeration and economic geography: spatial selection and sorting [J]. Journal of Economic Geography, 6(3):323-346. BEHRENS K, DURANTON G, ROBERT-NICOUD F. 2014. Productive cities: sorting, selection, and agglomeration [J]. Journal of Political Economy, 122(3):507-554. BEHRENS K, ROBERT-NICOUD F. 2014. Survival of the fittest in cities: agglomeration, polarization, and income inequality [J]. Economic Journal, 124(581):1371-1400. CICCONE A, HALL R E. 1996. Productivity and the density of economic activity [J]. American Economic Review, 86(1):54-70. COMBES P, DURANTON G, GOBILLON L. 2011. The identification of agglomeration economies [J]. Journal of Economic Geography, 11(2):253-266. COMBES P, DURANTON G, GOBILLON L, et al. 2012. The productivity advantages of large cities: distinguishing agglomeration from firm selection [J]. Econometrica, 80(6):2543-2594. FORSLID R, OKUBO T. 2014. Spatial sorting with heterogeneous firms and heterogeneous sectors [J]. Regional Science and Urban Economics, 46(3):42-56. FUJITA M, THISSE J. 2002. Economics of agglomeration: cities, industrial location, and regional growth [M]. Cambridge: Cambridge University Press. HARRIS C D. 1954. The market as a factor in the localization of industry in the United States [J]. Annals of the Association of American Geographers, 44(4):315-348. HEAD K, MAYERTT T, RIES J. 2002. On the pervasiveness of home market effects [J]. Economica, 69(275):371-390. HELPMAN E, MELITZ M J, YEAPLE S R. 2004. Export versus FDI with heterogeneous firms [J]. American Economic Review, 94(1):300-316. LEVINSOHN J, PETRIN A. 2003. Estimating production functions using inputs to control for unobservables [J]. Review of Economic Studies, 70(2):317-341. MARSHALL A. 1920. Principles of economics [M]. 8th ed. London: Macmillan Press. MARTIN P, ROGERS C A. 1995. Industrial location and public infrastructure [J]. Journal of International Economics, 39(3-4):335-351. MELITZ M J. 2003. The impact of trade on intra-industry reallocations and aggregate industry productivity [J]. Econometrica, 71(6):1695-1725. MELITZ M J, OTTAVIANO G I P. 2008. Market size, trade, and productivity [J]. Review of Economic Studies, 75(1):295-316. MELO P C, GRAHAM D J, NOLAND R B. 2009. A meta-analysis of estimates of urban agglomeration economies [J]. Regional Science and Urban Economics, 39(3):332-342. OKUBO T, PICARD P M, THISSE J. 2010. The spatial selection of heterogeneous firms [J]. Journal of International Economics, 82(2):230-237. OLLEY G S, PAKES A. 1996. The dynamics of productivity in the telecommunications equipment industry [J]. Econometrica, 64(6):1263-1297. OTTAVIANO G I P. 2011. ‘New’ new economic geography: firm heterogeneity and agglomeration economies [J]. Journal of Economic Geography, 11(2):231-240. PUGA D. 2010. The magnitude and causes of agglomeration economies [J]. Journal of Regional Science, 50(1):203-219. SAITO H, GOPINATH M. 2009. Plants′ self-selection, agglomeration economies and regional productivity in Chile [J]. Journal of Economic Geography, 9(4):539-558. SYVERSON C. 2004. Market structure and productivity: a concrete example [J]. Journal of Political Economy, 112(6):1181-1222. SYVERSON C. 2007. Prices, spatial competition, and heterogeneous:an empirical test [J]. Journal of Industrial Economics, 55(2):197-222. SYVERSON C. 2011. What determines productivity [J]. Journal of Economic Literature, 49(2):326-365.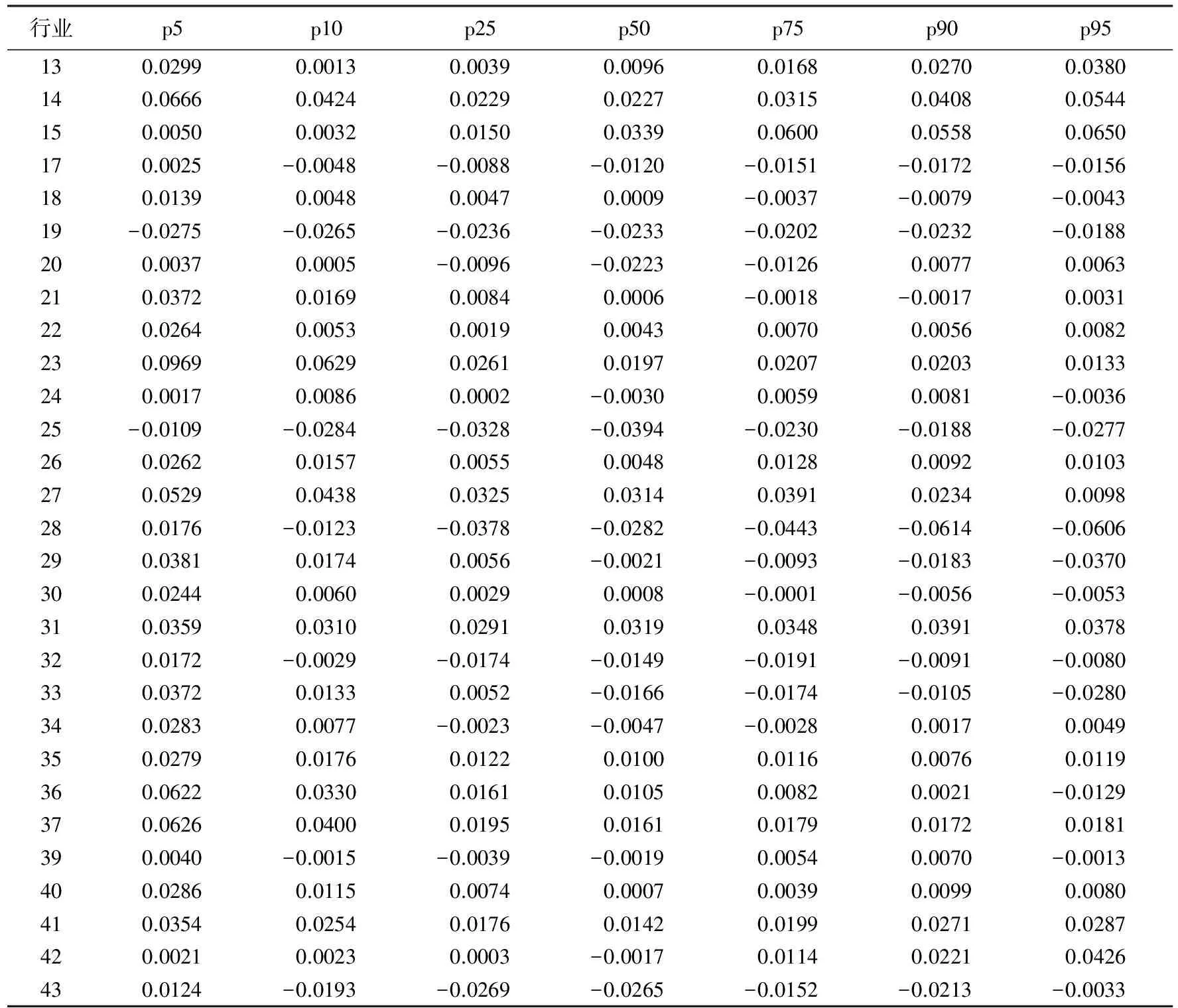
五、结论性评述
