错在哪里
2018-04-24佟成军,洪汪宝
1 江苏省海州高级中学
佟成军(邮编:222062)
题目在平面直角坐标系xOy中,已知圆C:x2+(y-1)2=5,A为圆C与x轴负半轴的交点,过A作圆C的弦AB,记线段AB的中点为M,若OA=OM,则直线AB的斜率为______.
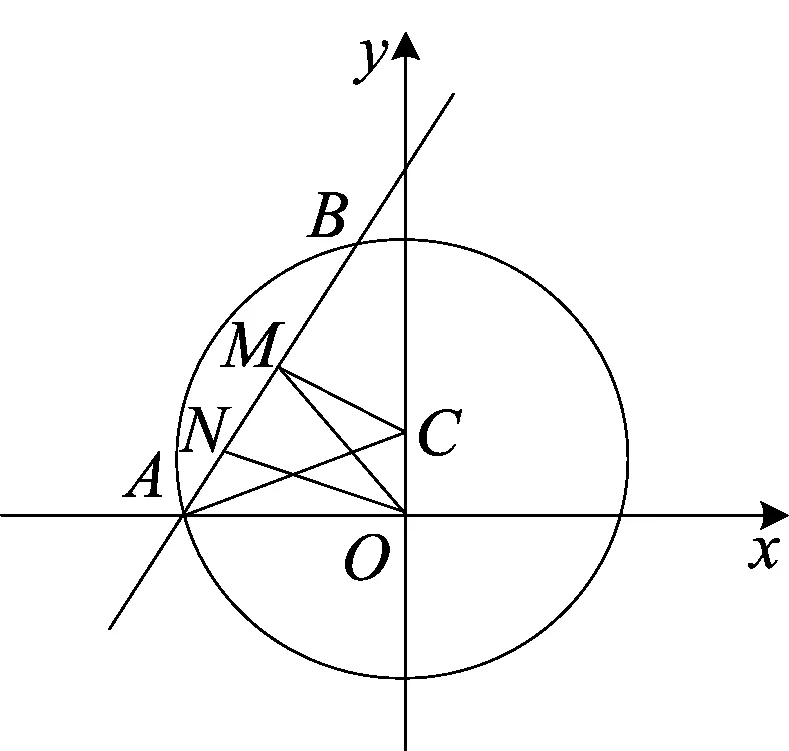
图1
错解如图1,取AM的中点为N,由OA=OM,知ON⊥AB.
由题意知CM⊥AB,且AM=2AN
①
直线AB的方程为y=k(x+2),
k≠-2.
②
在Rt△ACM及Rt△AON中,


两边平方整理得k2+4k-12=0,解得k=2或k=-6,满足②.
所以直线AB的斜率k为2或-6.

图2
解答错了!错在哪里?
错解中由题设条件OA=OM可以得到AM=2AN,但反之如何?由AM=2AN能一定得到OA=OM吗?如图2,
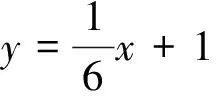
满足AM=2AN,但OA=OM不成立.
由此看到,错解是一种不等价的转化,是用必要条件解题的,对于结果必须要进行检验.
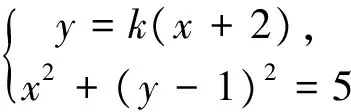
由△=[2k(2k-1)]2-4(1+k2)[(2k-1)2-5]>0,
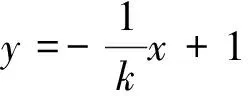
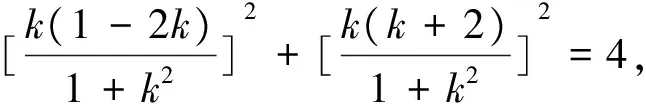
由k≠-2,知直线AB的斜率k为2.
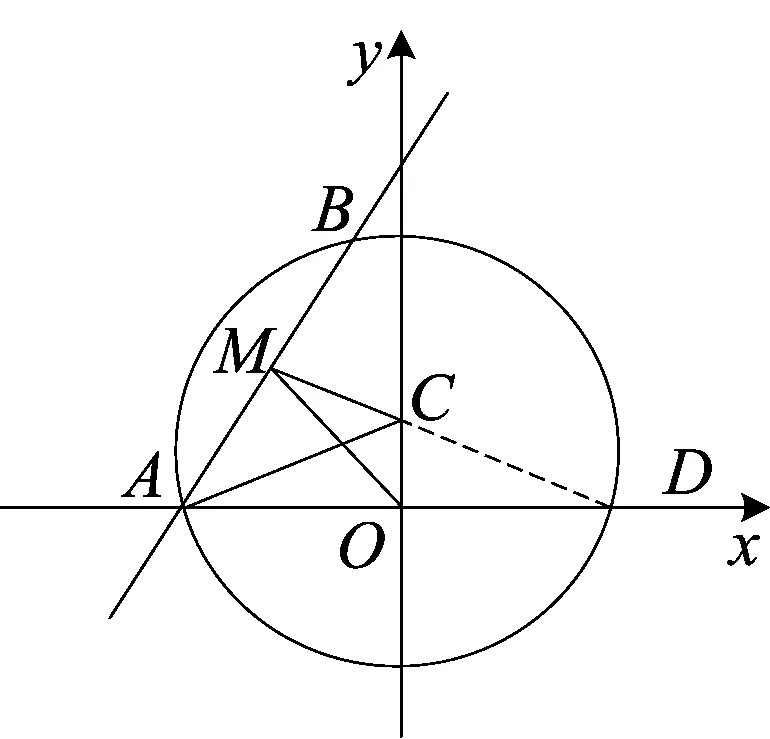
图3
正解2如图3,设D为圆C与x轴正半轴的交点,连结MD.
因为OA=OM=OD,所以点M在以AD为直径的圆上.
所以DM⊥AB.又CM⊥AB,所以M,C,D三点共线.

正解3设M(x,y),由OA=OM=2,得M点的轨迹为圆x2+y2=4,
又由CM⊥AB,得M点的轨迹为圆x(x+2)+y(y-1)=0,
以上两圆方程相减得2x-y+4=0恰为两圆公共弦AM的方程,即为直线AB的方程,所以直线AB的斜率k为2.
2 安徽省安庆市第一中学
洪汪宝(邮编:246004)
题目锐角△ABC中,sinA=4cosBcosC,则tanAtanB+tanBtanC+tanCtanA的最小值是______.
解由条件知sinA=sin(B+C)=sinBcosC+cosBsinC=4cosBcosC,
两边同除以cosBcosC,得tanB+tanC=4,
在锐角△ABC中,因为tanA+tanB+tanC=tan(A+B)(1-tanAtanB)+tanC=-tanC(1-tanAtanB)+tanC=tanAtanBtanC,
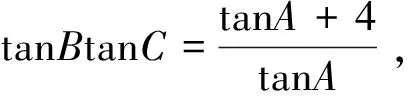
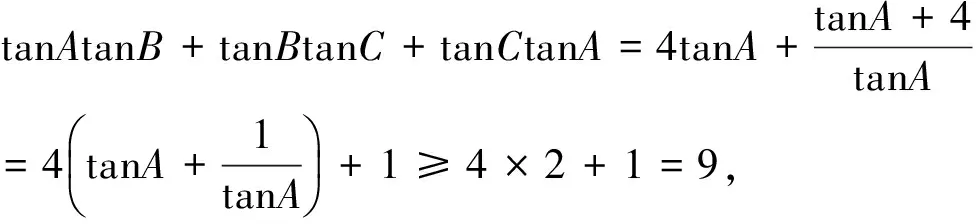

解答错了!错在哪里?
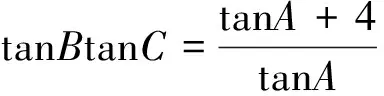
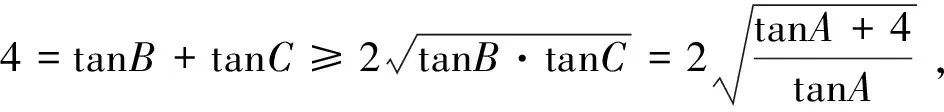
所以
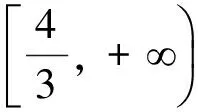
在运用均值不等式求最值时特别强调“一正二定三相等”这三个条件缺一不可,错解中也注意到了等号成立的条件,但没注意tanA,tanB,tanC三者之间的依赖关系导致出错,这种隐藏的关系要注意挖掘.
