一个几何问题的证明与推广

安徽省旌德中学

赵忠华 (邮编：242600)

南京师范大学数学与计算机科学学院

单 墫 (邮编：210024)

我在许康华微信公众号发了问题征解：

(1)直线MN过定点P；

(2)分别以AB和CD为直径作圆，则两圆相交弦XY中点R的轨迹是圆.

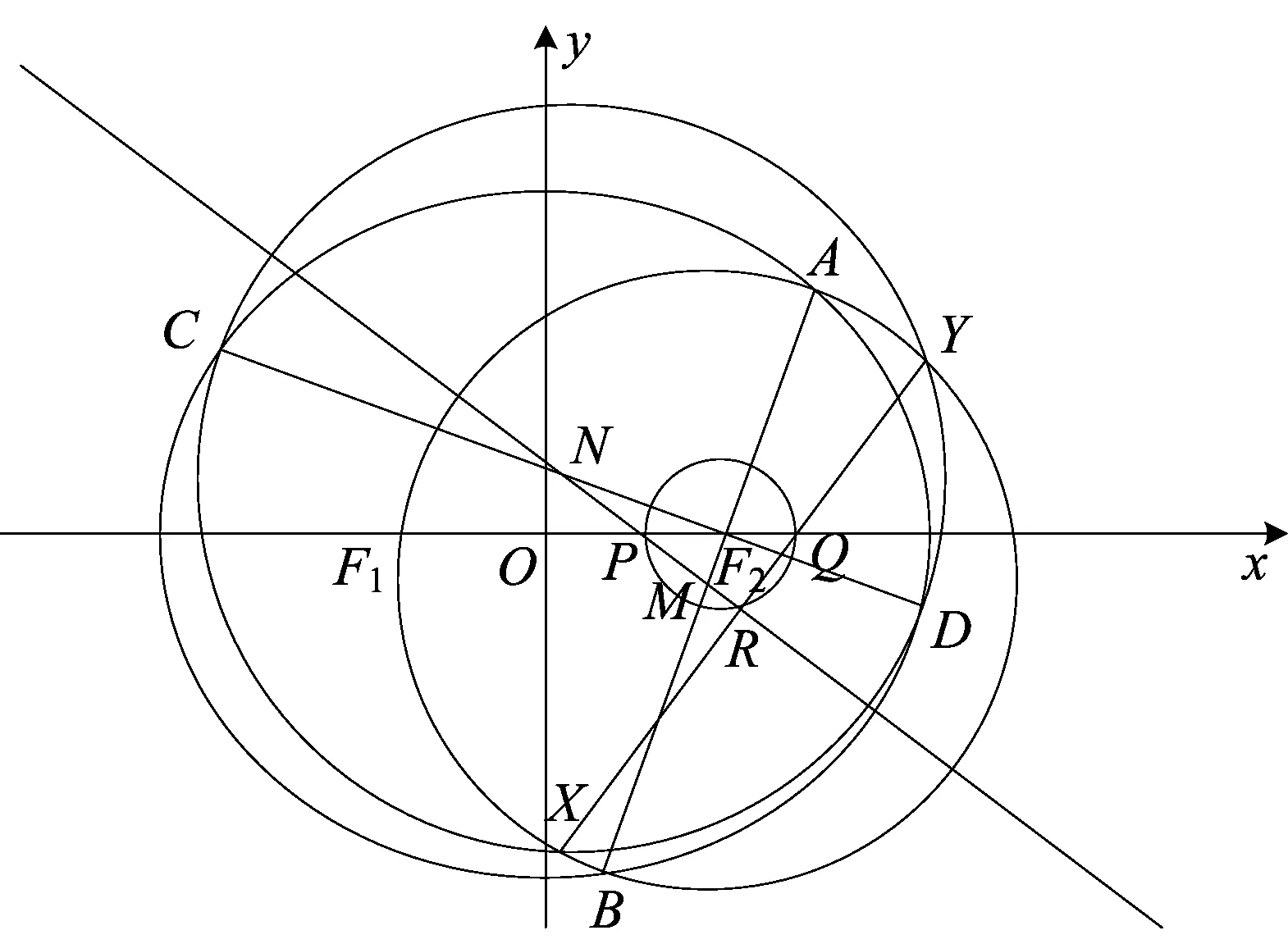
好多天过去了，没人给出解答，我自己给出一个证明，十分烦琐：

证明(1)设A(xA,yA)、B(xB,yB)、C(xC,yC)、D(xD,yD)、M(xM,yM)、N(xN,yN),

直线AB方程：y=k(x-c)代入椭圆方程化简得：(b2+a2k2)x2-2a2ck2x+a2c2k2-a2b2=0,

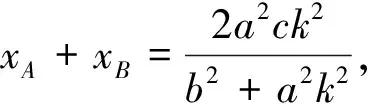
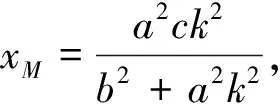
同理

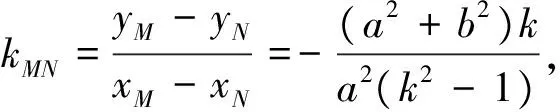
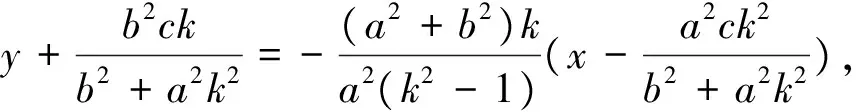
(2)以AB为直径的圆方程：(x-xA)(x-xB)+(y-yA)(y-yB)=0,即x2-(xA+xB)x+xAxB+y2-(yA+yB)y+yAyB=0

①

以CD为直径的圆方程：(x-xC)(x-xD)+(y-yC)(y-yD)=0,即x2-(xC+xD)x+xCxD+y2-(yC+yD)y+yCyD=0

②

由①-②可得两圆相交弦XY方程：[(xC+xD)-(xA+xB)]x+[(yC+yD)-(yA+yB)]y+xAxB-xCxD+yAyB-yCyD=0,又

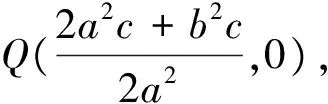
本命题对于抛物线，双曲线也成立，但证明均比较烦琐，数学届前辈单墫教授给出了一个统一证明，显示了非凡功力.

证明采用极坐标, 考虑一般的圆锥曲线. 不妨设焦点为左焦点F，x轴为极轴, 曲线方程为

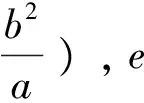
直线MN的方程为(用面积不难推出):

MN与极轴交点P的极半径ρ满足

XY是两圆的根轴, 点(ρ,θ)到⊙M的幂为

所以,XY的方程是

因为连心线MN⊥公共弦XY， 所以∠PRQ=90°，R在以PQ为直径的圆上.