打通纵横联系 巧构隐圆解题

江苏省新沂市第一中学

苗庆硕 (邮编：221400)

圆是一种非常完美的图形，具有很强的对称性和很优美的一些性质.因此，若能借助圆的一些性质进行解题，往往能达到化难为易的效果.笔者在教学过程中发现，有很多表面上看起来与圆无关的问题，若能通过细致的观察，实施一定的策略转化为圆的问题，往往能达到意想不到的效果，能突破解题的瓶颈.通过构造隐形的圆并转化为与圆有关的问题，体现了数形结合与化归的核心数学思想，是实数变式教学的重要途径与手段.下面结合近几年来的各类试题，谈谈如何构造隐圆解题这个问题，现分析如下，供大家参考.

1 双变量问题

解析令

其中a≥0，b≥0，则x=y+(x-y)=a2+b2.

图1

评注 本题含有两个变量与根式，通过观察，发现两个根式的平方和即为所求.通过实施换元策略，转化为常见的点与圆的最值问题，从而降低了解题的难度.

2 函数最值问题

图2

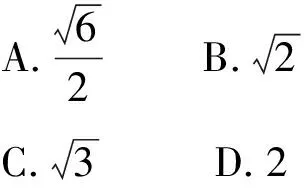
解析f(x)=

评注本题借助平面向量，构造隐圆，转化为与圆有关的向量数量积问题，令人耳目一新.

3 解三角形问题

例3(2008年高考江苏卷)满足条件

的三角形ABC的面积的最大值是______.

图3

解析以AB所在的直线为x轴，AB的垂直平分线所在的直线为y轴，建立如图所示的平面直角坐标系xOy，则可设C(x,y)，A(-1,0)，B(1,0).

评注本题若用解三角形的方法求解，要复杂得多.通过建系，发现点C在圆上运动，此圆是非常著名的阿波罗尼斯圆，是源于课本的一道经典考题.

4 平面向量问题

例4(2011年高考大纲全国卷)设向量a、b、c满足

〈a-c,b-c〉=60°，则|c|的最大值等于( )

图4

则

评注注意到向量具有数与形的特征，故可结合图形思考，不难发现O、A、C、B四点共圆，然后利用圆的性质和三角形全等的判定知识，实现问题的解决.

5 解析几何问题

例5(湖北省荆门、荆州、襄阳、宜昌2017年七校联考)已知圆O:x2+y2=4，点P为直线x+2y-9=0上一动点，过点P向圆O引两条切线PA、PB、A、B为切点，则直线AB经过定点( )

C.(2,0) D.(9,0)

图5

①

又圆O的方程为x2+y2=4

②

②减去①得两圆的公共弦AB所在直线的方程为2mx+2ny=4

③

因为点P(2m,2n)在直线x+2y-9=0上，所以2m+4n-9=0，即2m=9-4n.

所以③可化为(9-4n)x+2ny-4=0，即2n(y-2x)+(9x-4)=0，

评注通过观察，发现，A、O、B、P四点共圆，同时可求出此圆的方程.于是AB即为两圆的公共弦方程，两圆方程相减，即可快速得到直线AB的方程.这是源于课本的重要方法，应引起足够的重视.

通过以上的问题的分析，我们发现，构造隐圆解决数学问题是一种广泛运用于解题的方法.这种方法具有一定的可操作性，关键是通过认真观察，发现隐形的圆，使之为自己的解题服务.有些问题具有一定的数学文化背景，如例3，有些问题根植于课本而高于课本，如例5，有些问题打通了数学知识的内在联系，如例2.通过构造隐圆解决问题，不仅能开阔学生的思维与视野，提高解决问题的能力，还能使之体会到数学之美并学生的提高数学核心素养.