基于Qt与Matlab的行星齿轮传动系统故障监测诊断研究*

彭毓敏，栾忠权，马 超，徐小力

(北京信息科技大学 现代测控技术教育部重点实验室，北京 100192)

0 引言

行星齿轮箱是风力发电机组中的关键部件之一，由于其工作环境恶劣，常年受到不定风力和风向的变载荷作用，很容易出现故障和受到损坏。行星齿轮箱中的齿轮、轴、轴承等加工工艺复杂，装配精度要求高，又常常在高速度、变载荷下连续工作，故障率较高，是诱发机器故障的重要原因[1]。齿轮箱中的轴、齿轮和轴承在工作时会产生振动，一旦发生故障，其振动噪声信号的能量分布和频率成分将会发生变化[2]，存在大量的幅值调制及频率调制现象。Hilbert解调技术可以从复杂的振动信号中解调出其调制信号,在实际工程中得到了广泛的应用[3-4]。

近年来国内学者专家对齿轮箱的故障诊断系统及诊断方法进行了大量的研究，李怀俊应用LabVIEW，以齿轮传动系统的输入功率信号为处理对象，对能量信号监测与诊断系统进行了研究[5]；张积坚针对风力发电机齿轮箱的故障特征，运用在线编程技术，开发了基于 B/S 的风电机组在线监测系统并在风力发电机上进行了测试[6]；邓玉萍利用单片机控制技术、A/D 转换技术及数字滤波技术，对风机故障诊断监测系统的软件部分进行了设计，实现了对信号时域指标的计算和实时在线监测，使系统的抗干扰能力和准确性等方面有了很大的提高[7]；王聪使用Hilbert解调方法进行了齿轮箱点蚀故障的倒频谱研究[8]；罗毅分析了齿轮裂纹时振动信号为转速频率对啮合频率及其倍频调制的特点，运用小波包变换与倒频谱方法进行了风电机组齿轮箱齿轮裂纹诊断研究[9]。

近年来国内学者专家对齿轮箱的故障诊断系统及诊断方法进行了大量的研究[5-7]，他们主要从硬件控制电路、软件监测系统以及信号解调方法等方面展开了研究。通过使用Hilbert解调方法进行了齿轮箱点蚀故障的倒频谱研究[8]；运用小波包变换与倒频谱方法进行了风电机组齿轮箱齿轮裂纹诊断研究，分析了齿轮裂纹时振动信号为转速频率对啮合频率及其倍频调制的特点[9]。工程实际应用时，获取齿轮箱振动信号容易受到噪声的干扰，这些噪声有可能是在测量过程中传感器产生的，也有可能是机器运转时产生的，再就是受到周围环境的影响。这些因素都会使得测量的振动信号中带有噪声，如果噪声干扰过多将会降低信号的信噪比，严重时直接影响到故障诊断的结果。

研究针对行星齿轮箱故障监测诊断问题，考虑到干扰信号的影响，运用小波包去噪提高信号的信噪比，并结合Hilbert解调方法，进行了行星齿轮变速系统的故障诊断技术。运用Qt和Matlab在Windows系统下进行了信号采集分析系统开发研究，并运用实验室提供的行星齿轮传动系统实验台开展了不同工况下的试验验证分析。

1 基本原理1 小波包-Hilbert故障诊断原理

1.1 小波包去噪

小波包分析将频带进行多层划分，对信号低频部分和高频部分同时进行分解，并能够根据被分析信号的特征，自适应地选择相应频带，使之与信号频谱相匹配，提高了信号时频分辨率。小波分解中，分解级数越大，小波包尺度越大，小波包系数对应的空间分辨率就越低。

对信号进行小波包去噪一般按照以下步骤[10-11]进行:信号的小波包分解；确定最优小波包基，对于一个给定的熵标准，计算最优树；小波包分解系数的阈值量化；信号的小波包重构。上述步骤中，关键的是如何选取阈值和如何进行阈值量化，在一定程度上，直接关系到对信号进行去噪处理的质量。

1.2 Hilbert解调技术

假设齿轮啮合振动的载波信号为

xm(t)=Asin(2πfmt+ψ)

(1)

式中，fm为齿轮的啮合频率，ψ为载波信号的初相位。

齿轮轴旋转调制信号为：

xr(t)=1+mcos(2πfrt)

(2)

式中，fr为齿轮所在轴的转频。

设齿轮的振动信号为：

x(t)=Am[1+mcos(2πfrt)]sin(2πfmt+ψ)

(3)

Hilbert变换的目的就是要把幅值调制信号Am[1+mcos(2πfrt)]分离出来，x(t)的Hilbert变换为:

(4)

定义x(t)的解析信号为：

(5)

(6)

为振动信号x(t)的包络，对幅值Am(t)进行幅值频谱分析。

研究中将小波包去噪技术和Hilbert解调技术综合利用，进行了行星齿轮变速系统的故障诊断技术研究。在对原始信号进行去噪过程中，采用db3小波、软阈值法，对采集的信号进行3层分解处理，以提高信噪比。然后对去噪后的信号以其基频或者基频的倍频为中心进行窄带带通滤波，对滤波后的信号运用Hilbert再进行包络解调，最终得到最后的分析结果。

2 监测诊断系统设计

2.1 系统硬件构成

系统硬件主要包括采集模块、调理电路模块。采集模块又包括数据采集卡和振动信号传感器。本系统中采用的以太网数据采集卡 BC0816N(V6360D)如图1所示，实现具有8路路差分16位高精度同步模拟信号采集功能，在-10V ～+10V输入范围增益为1的情况下测得电压值只有1mV以下的误差。同时，单通道采样频率可高达50kHz。

图1 以太网数据采集卡

系统开发中主要使用了振动加速度传感器，选择加速度传感器应该将其线性频率范围作为重要因素考虑其中，该频率范围覆盖试验所关注的最低频率的0.2倍到最高频率的3.5倍[12]。本系统主要对行星齿轮箱的齿轮、主轴等重要部位进行信号监测，啮合频率大概范围为0Hz～1375Hz。本系统采用型号为YH411-26的三向ICP加速度传感器，如图2所示。

图2 ICP加速度传感器

为了保证数据采集过程中传感器的供电、滤波等问题，使用本实验室自行开发的 调理电路板，如图3所示。该调理电路板包含4个通道ICP放大电路及7阶抗混叠低通滤波器，可通过通道的跳线冒选择接入信号的类型，从而实现4通道ICP加速度传感器电压(0～10V)信号接入，并且可以对采集的信号实现(0.01～100)倍数放大，电源可选择±12V或者±15V交流电压。

图3 FILAMP-4型ICP调理电路板

2.2 系统软件设计

本系统以跨平台软件Qt和数值分析软件Matlab为软件开发工具，在Windows系统下运行。行星齿轮箱监测诊断软件结构框图如图4所示，具有实时采集、显示、保存、处理功能。

图4 监测系统软件结构图

系统软件主要分为采集系统软件和分析系统软件两部分，采集系统软件主要有登陆界面、主界面、采集显示界面组成。软件运行主界面如图5所示。点击系统主界面不同功能按钮，可以切换到不同运行界面，实现不同功能需求。点击采集数据按钮就会切换到采集显示界面，如图6所示。在采集信号之前需要进行一些基本的参数设置，比如文件保存路径、实验名称、试验对象、采样频率、通道参数等，参数设置的界面如图7所示。实时采集行星齿轮箱被测点的振动信号并以实时曲线的方式显示在采集界面上，更直观有效的把信息传达给用户，方便用户观察信号特征，做出初步判断。根据用户需求，可以将实时监测数据进行存储，方便后续的查询、分析。

图5 监测系统软件主界面

图6 信号采集显示界面

图7 参数设置界面

3 试验研究

3.1 实验工况

采用现代测控教育部重点实验室的风机行星齿轮传动平台进行试验验证。电动机采用YS1.5KW-4P电磁调速电动机，额定转速：125～1250r/min，额定转矩：19.2N/m；齿轮箱型号 HS-300，增速比：77.3；4个振动加速度传感器分布在HS-300齿轮箱上，搭建的测试系统如图8所示。三级行星齿轮箱传动系统的机构简图如图9所示。

图8 行星齿轮箱传动实验台

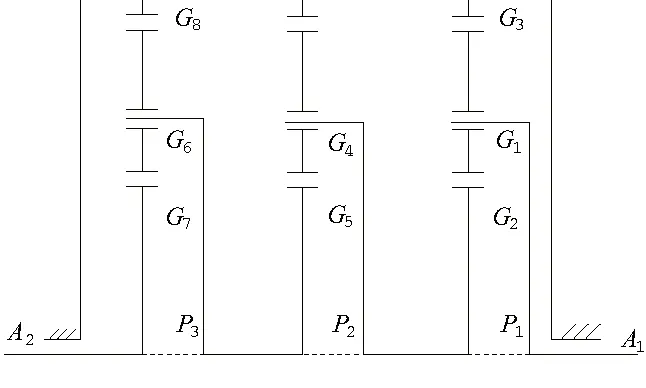
图9 行星齿轮箱传动机构简图

其中A1是输入端，A2是输出端；P1、P2、P3分别代表行星齿轮箱第一级、第二级和第三级的行星架；G2、G5、G7分别代表行星齿轮箱第一级、第二级和第三级的太阳轮；G1、G4、G6分别代表行星齿轮箱第一级、第二级和第三级的行星轮；G3、G8分别代表行星齿轮箱第一级、第二级和第三级的内齿圈，其中第二级和第三级共同使用一个内齿圈；行星齿轮箱各齿轮参数如表1所示。本实验为了更好的研究在不同工况下行星齿轮箱传动系统的运行状态，对其在不同转速、不同测点的不同方向下进行了振动信号采集。实验中行星齿轮箱的运行状态为轻微磨损，输出转速从540rpm逐步增加到840rpm，步长为60rpm。采样频率为20kHz，采样时间为10s。当行星齿轮传动系统输出轴A2转速为660rpm时，由行星齿轮箱的齿轮参数可以计算出齿轮箱各齿轮转频及啮合频率如表2所示。

表1行星齿轮箱各齿轮参数

齿轮齿数模数齿宽变位系数压力角G1212．25130．1120G2192．25130．1120G3621．7516-0．1520G4/G6211．75130．1420G5/G7191．75130．1620G8621．7554-0．0720

表2 各齿轮转频及啮合频率

3.2 实验结果分析

对行星齿轮箱输出轴A2转速为660rpm下采集的数据进行处理分析，应用开发的分析系统得到的原始振动信号时域图以及频谱图如图10和图11所示。

图10 原始信号时域图

图11 原始信号频谱图

对原始信号进行小波包去噪处理后其时域图以及频谱图如图12和图13所示。

对比图10和图12可以看出，经过小波包去噪后原始信号中的干扰噪声被有效地滤除，留下的信号为无污染的振动信号。从去噪后的信号时域图中，更能明显的看出信号的不平稳性且存在周期性的冲击信号。对比图11和图13可以看出，经过小波包去噪处理后，把原始信号中的高频干扰噪声滤除掉了。对去噪后的信号再进行更深入的分析，减少了无用信号的干扰，更有利于提取出与行星齿轮箱故障有关的特征频率。从图13中并不能准确地看到低频处幅值较高的几个值对应的频率，为此对去噪后信号的频谱进行细化得到图14所示。

图12 去噪后信号时域图

图13 去噪后信号频谱图

图14 频谱细化图

从图14中可以看到161.0 Hz、319.5 Hz、480.1 Hz、640.4 Hz、799.6 Hz、960.8 Hz附近处幅值较高，而它们基本近似为第三级啮合频率的1倍频、2倍频、3倍频、4倍频、5倍频和6倍频。并且从图14中可以明显看到在这些倍频附近存在很多边频带，由此可以初步判定行星齿轮箱第三级出现了早期的啮合故障，但是无法确定具体故障部件。为了准确的找出故障位置，分别以第三级啮合频率的1倍频160 Hz和2倍频320 Hz为中心频率进行窄带带通滤波，并对滤波信号进行Hilbert变换,解调出原始信号中的调幅信号,得到的解调谱如图15所示。

在图15所示的解调谱中，主要调制频率成分为11Hz、22 Hz、33 Hz、43Hz，他们基本是以11 Hz为基频的谐波成分，由表2可知11 Hz正好是第三级太阳轮G7的转频。由齿轮振动信号的频率特性及Hilbert解调原理可以判定是第三级太阳轮G7出现了故障。在拆开检查时，证实是第三级太阳轮G7出现了轻微磨损故障。

(a)对160Hz为中心频率带通滤波解调

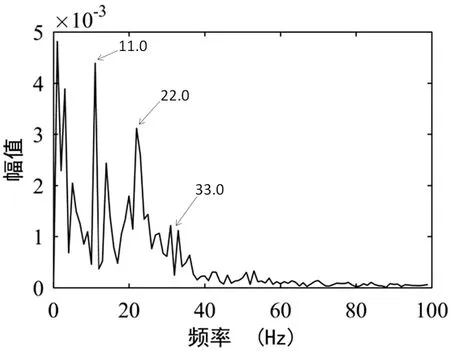
(b)对320Hz为中心频率带通滤波解调图15 Hilbert解调谱

4 结论

(1)试验结果表明通过对采集数据的时频域分析运用小波包去噪和Hilbert解调技术能够实现对行星齿轮箱的故障诊断，并初步对故障进行位置确定。研究结果表明：该方法在行星齿轮传动系统故障诊断中切实有效，可为行星齿轮箱的故障诊断提供技术支持，具有一定工程应用价值。

(2)结合Qt与 Matlab开发的行星齿轮箱故障监测诊断系统，能够实现对齿轮箱被测点振动信号的实时采集、显示、数据保存功能，系统界面良好，可交互性强，具有一定的实用价值。

[参考文献]

[1] 韩龙,王丽,朱显辉,等. 基于zig Bee和LabVIEW的风电机组齿轮箱监测诊断系统[J]. 自动化与仪器仪表,2015(9):105-106.

[2] 陆人定. 齿轮箱故障时域和频域诊断综合技术[J]. 机电工程技术,2005(1):17-19.

[3] 姚志斌,沈玉娣. 基于Hilbert解调技术的齿轮箱故障诊断[J].机械传动,2004,28(2):37-39.

[4] 刘尚坤,唐贵基.小波降噪与Hilbert解调相结合的齿轮箱故障诊断方法[J].机械工程师,2014(4):103-105.

[5] 李怀俊. 齿轮系统的能量信号监测与故障诊断系统研究[J].实验技术与管理,2015,32(6):90-93.

[6] 张积坚,王奉涛. 风力发电机组齿轮箱在线监测系统的开发[J].工业控制计算机,2009,22(12):49-50.

[7] 邓玉萍,田继宏. 风机故障诊断监测系统软件设计[J].鞍山师范学院学报,2016,18(6):35-37.

[8] 王聪. 基于 Hilbert解调及倒谱的齿轮箱点蚀故障诊断研究[J].电力科学与工程,2011,27(3):36-40.

[9] 罗毅，甄立敬. 基于小波包与倒频谱分析的风电机组齿轮箱齿轮裂纹诊断方法[J].振动与冲击,2015,34(3):210-214.

[10]Deboer DW. Drop and energy characteristics of a rotating spray plate sprinkler [J]. Journal of Irrigation and Drainage Engineering, 2002, 6:137-146.

[11] GuR. Modeling two-dimentional turbulent offset jets[J].Journal of Hadraulic Engineering, 1996,11:617- 624.

[12] 张杰.振动测试加速度传感器的选择和固定[J]. 环境技术,2013(s2):86-88.