柔顺并联机构结构优化与动力学仿真*

赵 元，杜 莹

(沈阳工学院 a.机械与运载学院； b.基础课部，辽宁 抚顺 113122)

0 引言

近年来，柔顺机构已经成为精密超精密运动系统中定位平台的常用解决方案。柔顺机构是一种利用运动构件中构件自身的弹性变形，从而实现定位机构的运动传递、力传递及转换的机构。由于弹性变形具有可逆性，构件自身受到力作用产生变形，卸除载荷后变形消失，实现传递变形的同时保证不会产生摩擦磨损和传动间隙[1-2]。柔顺机构的设计主要分为两种，并联和串联。其中，柔顺并联机构能够克服反向间隙、迟滞效应以及铰链加工误差等缺陷，并且承载能力大、定位精度高、分辨率高以及操作灵活等优点，从而柔顺并联机构广泛应用于超精密定位以及微纳制造领域[3-4]。然而，柔顺关节传递位移较大，降低了在非运动方向的刚度，从而影响了其动态特性。因此，具有较高的刚度比、大的工作空间以及快速的动态相应的多自由度柔顺并联机构设计仍然是柔顺机构领域内的重要研究课题。

为得到较为理想的柔顺并联机构，国内外研究学者针对柔顺机构的设计、自由度数目、刚度优化方法以及动力学优化方法进行了相关研究，并得到了较为显著的成果。传统柔顺并联机构是通过铰接在刚体运动机构上不同的柔顺铰链，形成全柔顺并联机构。但是这种方法得到的机构复杂性较高，刚度分析和动力分析太过复杂，且无法满足超精密定位及微纳制造的需要[5-6]，另外还有多自由度柔顺并联机构的设计等[7-9]。针对柔顺机构的结构分析方法，Midha等[10]提出了伪刚体模型法，主要通过用两根相铰接的刚性杆模拟柔性片段的弯曲变形，刚性杆末端轨迹可以通过改变铰接点位置和扭簧的刚度逼近柔性片段的轨迹。该模型法在柔顺机构的研究中具有较高的精度，但是不能真实的反应柔顺并联机构的刚度和动力学优化过程，不能满足精密定位的技术要求[11]。朱大昌等[12]提出一种多支链组合成新型全柔顺并联机构，利用柔性铰链集成在一块整体材料上，经线切割加工得到整体集成式机构，但柔性铰链的整体分布没有固定规则，具有较强的随意性，因此提出一种针对柔顺并联机构刚度和动力学优化的结构优化方法具有实际意义。

本文提出针对多自由度柔顺并联机构刚度优化和动力学特性优化的新的优化方法，包括刚度优化与动力学优化两个过程，称为梁结构优化方法。刚度优化过程中对弯-扭梁结构的参数进行优化，同时对刚度矩阵每个元素单位进行统一，动力学优化的目的是在保持最佳刚度的同时获得所需要的结构动态特性。为了验证该方法的有效性，综合3自由度柔顺并联机构并利用Matlab遗传算法求解器和ANASY有限元仿真软件对其进行计算以及仿真分析。

1 基于梁的结构优化方法

1.1 梁的结构优化原理

柔顺并联机构包括由数个柔顺关节联接的移动平台，柔顺关节作为无摩擦支撑轴承。为综合多自由度空间运动柔顺并联机构，提出一种新的基于梁的结构优化方法对各柔顺关节结构进行优化。以具有3个柔顺关节的柔顺机构为例，如图1所示。3个柔顺关节关于移动平台中心旋转对称，柔顺关节的设计为立方体，其中与移动平台联接的面为可移动联接面，与其相对应的为固定面。在每个柔顺关节空间中设置初始柔顺结构为弯-扭梁，如图2a。由于本文提出的结构优化方法适用于综合多自由度的柔顺并联机构，因此弯-扭梁的弹性变形可以为每个柔顺关节提供至少6个自由度。其中，贝塞尔曲线基于理想运动轨迹为每个柔顺关节提供可行解。为计算弯-扭梁的初始方位和扭转性能，设置梁的初始扭转角和最终扭转角，因此，在自由端运动联接面可以实现6个自由度。然后，以一个薄矩形截面区域沿三次贝塞尔曲线进行扫面，同时改变两端的方向就可以得到特定的几何结构，如弯-扭梁。另外，相比于其他的曲线结构如螺旋线等，具有初始扭转角的贝塞尔曲线也可以改变成任何形式的弯曲结构(如传统的直梁型)，这也是选择贝塞尔曲线作为弯-扭梁结构生成扫描路径的主要原因。如图2a所示，当贝塞尔曲线中两个控制点呈一条直线时，也就是初始扭转角αA和最终扭转角αB等于零，以薄矩形截面区域扫描贝塞尔曲线得到的梁结构为直梁型结构。具体柔顺关节空间设计为沿Y′Z′平面对称的两个弯-扭梁作为主要柔顺结构，如图2b。

以上分析可知，弯-扭梁的形成是用薄矩形截面区域对沿Y′Z′平面对称的三次贝塞尔曲线扫描得到的，起始点和终点分别曲线上的A点和B点。参照图2a，定义弯-扭梁上任意位置上的局部加载点的坐标系，其中，Z′轴对应贝塞尔曲线的切线方向，X′轴为整体加载点坐标系X轴在平面X′Y′平面上的投影。X′轴与矩形截面区域的长边之间的夹角成为扭转角，如初始扭转角和最终扭转角定义为αA和αB。

图1 三关节柔顺并联机构示意图

(a)弯-扭梁

(b)柔顺关节图2 结构示意图

基于弯-扭梁的结构优化过程如下：首先，定义柔顺并联结构的自由度以及弯-扭梁的初始参数，如边界尺寸和矩形界面区域的初始参数等；其次是为刚度优化过程定义柔顺关节的几何设计变量，刚度优化的目的是求出刚度矩阵的最优适应度函数，如式(10)。该过程中，为找到最佳的弯-扭梁几何结构预先定义其截面参数而不考虑其附加质量，从而为柔顺并联机构目标工作空间提供一个最优刚度比；然后进行动态相应优化，考虑到弯-扭梁截面区域面积参数、梁附加质量分布和位置来制定动态优化的设计变量。考虑到柔顺并联机构的高柔顺性和快速动态相应性是相互矛盾的，动态优化过程的适应度函数用式(13)表示，分别表示柔顺并联机构的对期望值的动态相应以及在最小化适应度函数值f的同时尽可能保证较高的刚度性能。最后，经过优化后的柔顺并联机构能够获得期望刚度值的同时得到最佳的动态相应特性。

1.2 刚度建模

刚度优化的目的是找到弯-扭梁结构的最优设计参数，从而使柔顺并联机构在目标工作空间和尺寸约束的前提下达到最高的刚度比。利用有限元分析方法将梁离散成为若干段，每一部分都代表标准梁单元。假设所有柔顺关节对称且相同，则弯-扭梁共存在14个设计参数作为刚度优化的设计变量。其中基于坐标系(xi,yi,zi)和4个控制点定义贝塞尔曲线结构的参数有12个，剩余两个则代表弯-扭梁的扭转角。

每个梁单元刚度矩阵可以表示为Ke，那么设柔顺并联机构中有N个梁单元，则整个柔顺并联机构的总体刚度矩阵可以表示为下式：

(1)

进一步，柔顺并联机构6×6刚度矩阵可以写成以下基本形式：

(2)

结合施加在移动平台上的外部载荷P以及对应的位移向量U(Δx,Δy,Δz,θx,θy,θz)，上式可以表示为：

(3)

KU=P

(4)

柔顺并联机构的自由度集为D={1,2,…,6}，6自由度柔顺并联机构中数字1,2,3分别表示三个沿X、Y和Z轴运动的直线自由度；4,5,6分别表示绕X、Y和Z轴转动的三个转动自由度。另外，N和M分别表示期望自由度集和非期望自由度集，即N∪M=D，分别用η和μ表示其个数。同时Pi和Ui、Pj和Uj为期望自由度和非期望自由度对应的载荷和位移。由此可知对应的做功为：

(5)

(6)

式中,Ki(或Kj)代表第i(或第j)个组件中对角线刚度矩阵。

对于特定自由度的柔顺并联机构，用单个期望做功值与全部组件的非期望做功值的比值表示机构的运动解耦能力，用R表示其比值关系，具体如下式：

(7)

根据式(5)和式(7)，表示柔顺并联机构最佳刚度值的最小适应度函数值f可以表示为：

(8)

给定柔顺并联机构的自由度，通过期望做功值可以实现最大化机构的工作空间，对应的机构运动解耦能力可以通过增大期望自由度和非期望自由度之间的刚度比实现最大化。

1.3 动态建模

动力学优化的目的是实现机构的目标相应，也就是一阶共振模式。主要包括两个方面，一是弯-扭梁的矩形横截面参数，二是柔顺并联机构的材料分布情况，具体见图3。由图可知，代表弯-扭梁设计变量参数值有6个，分别为弯-扭梁矩形横截面参数(b1,h1)，附加质量块横截面参数(b2,h2)，以及附加质量块的位置和尺寸参数(P,L)；表示移动平台参数变量有2个(R,T)。

每个梁单元的质量矩阵用Me表示，则整个柔顺并联机构的质量矩阵可以表示为：

(9)

其中，柔顺并联机构的固有频率可以表示为F，则频率向量可以表示为下式：

(10)

(a)弯-扭梁结构 (b)移动平台图3 动态优化基本参数

提高柔顺并联机构装置的刚度可以获得机构的最佳动态响应。动态优化的目标是综合多自由度柔顺并联机构以获得目标一阶共振频率，此时F1=Fd。动力学数学模型中适应度应满足两个条件，一是保持较高的刚度比，另外一个条件是获得该机构的最佳质量分布。因此，动态优化过程中的适应度函数可以用下式表示：

(11)

2 自由度柔顺并联机构优化

以3自由度柔顺并联机构(θx-θy-Z)为例对提出的结构优化算法进行分析。柔顺并联机构的最小工作空间设置为5°×5°×5mm，最小刚度比和理想一阶共振频率分别为100和100Hz，移动平台材料为Al7075-T6，杨氏模量为71.7GPa，泊松比0.33，密度为2.81g/cm3以及屈服强度为503MPa。柔顺关节设计空间为50×50×50mm3，弯-扭梁分为15个梁单元。

2.1 刚度优化

刚度优化过程中得到的柔顺并联机构的刚度矩阵为对角占优矩阵，也就是说在3自由度柔顺并联机构中，对角占优矩阵中第3、4和5个对角分量分别对应期望自由度Z、θx和θy。相应的期望自由度与非期望自由度可以表示为N={4,5,3};η=3和M={1,2,6};μ=3。则相应的做功可以表示为：

(12)

(13)

适应度函数为：

(14)

若P为单位载荷，相当于κ=1，则上式可以简化为：

(15)

根据刚度优化过程中的变量参数设置，定义适应度函数初始参数值以及各变量的取值范围，利用Matlab遗传算法工具箱求解器进行求解。由刚度优化过程合成得到的单个柔顺关节如图4a所示，由图可知，该单个柔顺关节扭转角为零。通过设置两个弯-扭梁之间不相交这一约束条件，可以在刚度优化过程中避免减小误差，两个弯-扭梁之间的偏移量设置为1mm。基于优化设计变量，对合成的柔顺并联机构进行3D模型的建立，如图4b。得到柔顺并联机构的柔顺矩阵Cs，则刚度优化过程可以表示为下式：

(16)

(a)单个柔顺关节 (b)柔顺并联机构图4 刚度优化结构

2.2 动力学优化及仿真

根据本文提出的柔顺并联机构机构优化方法对其进行动力学优化，从而得到多自由度柔顺并联机构的质量分布优化结构。机构的目标固有频率为100Hz，同样利用Matlab遗传算法工具箱求解器进行多目标动态优化。图5a为最终得到的柔顺并联机构3D模型，利用ANASY有限元仿真软件对其进行动力学仿真得到的一阶共振模态，其结果符合目标值100Hz，如图5b。动力学优化得到的柔顺矩阵Cd为：

(17)

根据柔顺矩阵得到刚度比为：

(18)

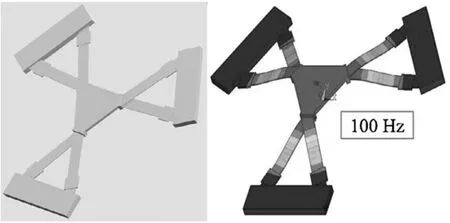
(a)柔顺并联机构3D模型 (b)仿真分析一阶模态 图5 柔顺并联机构

根据式(17)和(18)可知，由于柔顺矩阵对角线元素相对于非对角线元素大，综合的多自由度柔顺并联机构具有良好的运动解耦能力。同时刚度比较大，对应该机构具有较大的工作空间。ANASY数值仿真过程中屈服强度设置为503MPa，工作空间能够达到8°×8°×5.5mm，其中，相较于优化前的柔顺并联机构，对其进行刚度优化和动力学优化后的柔顺并联机构中弯-扭梁的扭转角度提高了60%，机构伸长量增加了10%，因此，相比目标工作空间有较大的提升。因此，基于梁机构优化方法得到的3自由度柔顺并联机构不仅仅能够得到较好的刚度，而且还能保持较高运动解耦能力的同时获得较大的工作空间。

3 结论

本文提出针对多自由度柔顺并联机构刚度优化和动力学特性优化的新的结构优化方法，包括刚度优化与动力学优化两个过程，称为梁结构优化方法。该柔顺并联机构主要由移动平台和3个柔顺关节空间组成。柔顺关节空间中，每个柔顺关节通过一组相互对称的弯-扭梁进行铰接。刚度优化过程中对弯-扭梁结构的参数进行优化，同时对刚度矩阵每个元素单位进行统一，动力学优化的目的是在保持最佳刚度的同时获得所需要的结构动态特性。为了验证该方法的有效性，综合3自由度柔顺并联机构(θx-θy-Z)并利用Matlab遗传算法求解器和ANASY有限元仿真软件对其进行计算以及仿真分析。计算结果和仿真结果显示，优化得到的3自由度柔顺并联机构不仅能够实现较大的工作空间8°×8°×5.5mm，而且其移动刚度比和转动刚度比分别大于200和4000。

本文提出的柔顺并联机构优化方法不仅仅局限于3自由度的柔顺机构的优化过程，同时也为合成更高自由度柔顺并联机构提供了基础，如5自由度以及6自由度。另外，合成柔顺并联机构的新方法也将用于探索3D打印技术实现复杂几何形状的制备等问题。

[参考文献]

[1] Howell, Larry L, Spencer P Magleby, et al. Handbook of compliant mechanisms [M]. John Wiley & Sons, 2013.

[2] 张连杰, 刘善增, 朱真才. 柔顺机构的研究进展[J]. 组合机床与自动化加工技术, 2011(7):108-112.

[3] 孙炜. 新型大行程柔顺并联机构理论与实验研究[D]. 广州:华南理工大学, 2014.

[4] 孙文结. 平面全柔顺并联机构构型拓扑优化设计[D]. 赣州:江西理工大学, 2014.

[5] 李杨民, 肖宵, 汤晖. 一种新型3自由度大行程微定位平台设计与分析[J]. 机械工程学报, 2013,49(19): 48-54.

[6] 余跃庆, 崔忠炜, 赵鑫, 等. 柔顺关节并联机器人设计与实验[J]. 农业机械学报, 2013, 44(7): 274-278.

[7] Li X, Tian Y, Qin Y, et al. Design, identification and control of a 2-degree of freedom flexure-based mechanism for micro/nano manipulation[J]. Nanoscience and Nanotechnology Letters, 2013, 5(9): 960-967.

[8] Bhagat U, Shirinzadeh B, Clark L, et al. Design and analysis of a novel flexure-based 3-DOF mechanism[J]. Mechanism and Machine Theory, 2014, 74: 173-187.

[9] Liang Q, Zhang D, Chi Z, et al. Six-DOF micro-manipulator based on compliant parallel mechanism with integrated force sensor[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(1): 124-134.

[10] Midha A, Norton T W, Howell L L. On the nomenclature, classification, and abstractions of compliant mechanisms[J]. Journal of Mechanical Design, 1994, 116(1): 270-279.

[11] ZL Guo, TJ Teo, HY Song, et al. Structural optimization for flexure-based parallel mechanisms-Towards achieving optimal dynamic and stiffness properties[J]. Precision Engineering, 2015, 42: 195-207.

[12]朱大昌, 宋马军. 平面整体式三自由度全柔顺并联机构拓扑优化构型设计及振动频率分析[J]. 振动与冲击, 2016, 35(3): 27-33.

(编辑李秀敏)