基于OpenGL的立铣刀螺旋槽参数化建模系统研究*

娄志超，赵先锋，史红艳，姜雪婷

(贵州大学 机械工程学院，贵阳 550025)

0 引言

立铣刀作为一种高性能的自由曲面加工刀具，具有良好的切削加工性能和加工表面质量，在航空航天、汽车、模具等行业广泛使用。但是由于立铣刀结构复杂，规格繁多，螺旋槽复杂曲面的设计算法复杂，人工计算工作效率较低，因此可利用CAD技术对刀具设计进行参数化的开发。近些年，随着国内外众多优秀的商业化三维建模软件的发展和广泛应用(达索公司的CATIA和SolidWorks、西门子公司的UG以及PTC公司的Pro/Enginee等)，为复杂刀具的建模系统的实现提供了新的平台，国内相应的展开了针对复杂刀具三维建模技术的研究工作。米蓉[1]基于CATIA和UG二次开发技术建立了基于加工过程的整体式立铣刀三维模型；赵鑫[2]通过UG/Open二次开发工具实现了锥度球头铣刀的设计；熊烽[3]基于Matlab软件，进行数学建模，绘制设计图形一种等螺旋角、等前角圆锥球头立铣刀；李宏德[4]基于PRO/E软件，对立铣刀螺旋容屑槽的法向截形参数与立铣刀螺旋角与截面旋转角的关系进行分析，实现立铣刀实体建模；赵先锋[5-6]利用包络原理在SolidWorks的基础上进行二次开发，建立了立铣刀的三维模型，其螺旋槽截面图形和Walter的截面图形完全一致；然而上述研究大多通过商业软件绘图软件进行二次开发，依赖于国外软件的图形系统，没有自主知识产权，具有很大的应用局限性。

OpenGL是个基层图形库，如商业软件中CAD、UG等三维建模软件都是以OpenGL图形库进行开发，通过OpenGL构建三维曲面[8]，将三维图形划分为点云，再进行点云的相互点之间的连接形成三角网格，将模型网格进行OpenGL渲染，以此实现立铣刀螺旋槽的建模[9]；并且OpenGL是个与硬件无关的软件接口，可以在不同的平台如Windows 7、Unix、Linux等之间进行移植。具有很好的移植性，可以获得非常广泛的应用。基于OpenGL的程序框架构造好后，用户只需要在对应的函数中添加程序代码即可，扩展性好，由于OpenGL是图形的底层图形库，不需要依赖于其他绘图软件的技术，具有独立性。

因此，本文在Visual Studio 2015平台下基于OpenGL研究开发立铣刀三维参数化建模软件，省略将商业建模软件作为搭建建模系统的中介，而直接由OpenGL底层图形库，采用点云进行三维曲绘制方法进行开发，并提出了以关键点进行数学建模的思想，通过改变关键点的位置实现立铣刀的三维建模；由于是从底层实现绘图，建模精确精度大大提高，建模效率也有提升。该软件以CAD工程图作为参考进行模型的绘制，可直接以CAD工程图进行参数的输入，方便快捷，具有较好的实用性；直接通过OpenGL进行建模，具有独立的技术体系和自主知识产权，具有广阔的市场应用前景。

立铣刀螺旋槽三维模型生成方式，如图1所示。

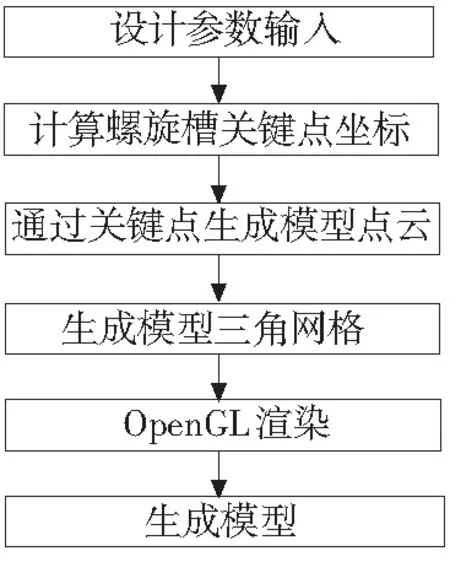
图1 立铣刀螺旋槽模型生成流程

1 OpenGL建模环境的搭建

由于OpenGL是个状态机的概念，需要通过创建OpenGL的渲染设备，并依次将其所需状态进行设置，使得OpenGL具有这些状态功能，从而在OpenGL环境下进行立铣刀建模系统的开发，由于OpenGL环境搭建文献与教程有很多，而且搭建OpenGL流程已成固定化，本文不再进行重述(参见文献[9-13])，而以视口方面进行阐述OpenGL的搭建过程。

1.1 OpenGL 视口的搭建

在OpenGL中包含俩个矩阵：projection和model view，其中又包含3个坐标系：世界坐标系、视口坐标系、屏幕坐标系；要使图形显示，就需要对坐标系进行一系列的矩阵变化，才能显示到屏幕上被观测到，如图2所示模型处理流程图。首先图形的建模是在世界坐标系下完成，由于计算机屏幕上只能表现二维平面，所以要使得立铣刀建模系统显示三维图形，需要在投影矩阵(projection)作用下把所绘制三维物体转到二维平面图像间的变换，投影矩阵会把所有的3D信息投影到2D屏幕上，此时，模型在视口坐标下，再通过模型视口矩阵(model view)对模型进行作用，从而转换到屏幕坐标系下，然后把模型投影到屏幕的范围内，才能使图形显示到屏幕上，其中投影的操作如同摄像机的原理，需要在摄像机拍摄范围内，镜头画面才有模型的显示。如此，所建模的立铣刀螺旋槽三维图形便可在屏幕中显示。

参考代码：

//设置矩阵

glMatrixMode(GL_PROJECTION);//告诉gpu显卡对投影矩阵进行操作；并进行投影矩阵设置

gluPerspective(50.0f, 800.0f/600.0f, 0.1f, 1000.0f);//对投影矩阵进行操作

glMatrixMode(GL_MODELVIEW);//设置模型视口矩阵

//模型的绘制代码

........

图2 模型处理流程

2 立铣刀螺旋槽截面建模

立铣刀螺旋槽参数如表1所示，首先以螺旋槽截面中心设为原点，搭建xy正交坐标系，如图3所示，通过计算与截面参数相关的所有关键点坐标，并将关键点进行依次连接实现螺旋槽截面建模。

分析螺旋槽截面形状及特征，将螺旋槽截面划分为几个关键点构成的线段或曲线。可知螺旋槽截面由关键点B、A、C、E、F、G、H共7点，如图3、图4所示，将关键点相互连接，形成线段或曲线再进行旋转即可得到完整的螺旋槽截面图形。

表1 立铣刀螺旋槽面截面相关参数

图3 立铣刀螺旋槽截面

图4 螺旋槽截面局部放大图

将铣刀截面中心设定在坐标原点，并把O2点设定为小圆弧AB的圆心，由此可知点C坐标为(0,L1/2),分别作辅助线CO，O2A，O2O，AO2，其中与坐标轴交于点D，如图3、图4所示，通过表1螺旋槽参数可求得：

L(BO)=L1-L4

(1)

∠(CDA)=90°-c

(2)

设线段DC为y值，线段CA为x值，那么在ΔACD中x与y的关系为x/y=cos(c)，而且通过ΔOO2D的关系，可知：

L(O2D)=y·sin(c)

(3)

L(O1D)=L1/(2-y)

(4)

L(OO2)=L/2-L4+L6

(5)

应用三角形余弦定理，构造一元二次方程，从而解出y与x的值。

A=sin2(c)

(6)

B=L1-L1·sin2(c)

(7)

(8)

通过式(6)～式(8)联立可得：

(9)

x=y·cos(c)

(10)

由此可知点A、C、D的坐标，点C坐标：(0,L1/2)；

点D坐标：(0,L1/2-y)；

而点A坐标可通过旋转法求得，在y轴取一点A1,A1C的长度为AC，则点A1坐标为(0,L1/2-x)，将点A1以C为圆心AC长度为半径逆时针旋转∠DCA(∠DCA=c)到AC所在直线上即可得到A点坐标。

B点坐标则可仍使用旋转法求解，先求出点O2的坐标，再由点A绕圆心O2以槽底圆弧L6顺时针旋转∠AO2B，由此可得点B坐标。

点B坐标具体解法：作辅助线O2M垂直于y轴，如图4所示，由式(9)、式(10)求得CA和DC长度，通过简单三角函数可推得∠(O2OC)=c，通过旋转法，从y轴选取点OO2长度，绕原点绕逆时针旋转c角，可得槽底圆弧AB的圆心O2点坐标，并由式(11)～式(13)推得式(14)，再由式(14)推出式(15)、式(16),即槽底圆弧起点A与终点B的角度∠sa与∠ea角度，通过∠sa与∠ea的差值，可得∠AO2B,由于已知小圆弧AB半径为槽底圆弧长度L6，逆时针旋转∠AO2B可得B点坐标。

a1=L6-y·sin(c)

(11)

b1=L6+L1/2-L4

(12)

c1=L1/2-y

(13)

通过式(11)～式(13)可得

(14)

通过式(14)可推出起始角度sa

sa=c-ap

(15)

ea=c

(16)

现已求得关键点坐标B、A、C,而点E、F、G可通过作辅助线EN，FP分别垂直于y轴，构建直角三角形ΔECN与ΔEUF，如图4所示，根据所给参数：螺旋槽第一后角宽度L2、螺旋槽第二后角宽度L3、螺旋槽第一后角a、螺旋槽第二后角b、刻背深度L5；直接利用直角三角形三角函数便可依次求得点E、F、G；而点H可将点B以OB长度为半径绕轴心顺时针旋转120°可得。

至此，单齿的螺旋槽截面关键点B、A、C、E、F、G、H坐标已全部计算完毕，将所有关键点绕原点旋转复制120°、240°可得螺旋槽截面所有关键坐标点；将关键点之间的线段，将截出的每个线段俩个端点，将这些端点以及所求出的关键点形成点云，点越多，模型绘制越精密，但是运行速度回会大幅度减慢，本文则直接将关键点进行连接，而其中如AB与GH不是直线段的圆弧段，需要采用微积分方法，将其圆弧分成若干个直线段，通过圆心、旋转角度和半径的信息，可依次求得圆弧中每一线段中的端点信息，进而求出AB与GH圆弧的点信息，由此可得到整个螺旋槽截面的点云信息。

3 立铣刀螺旋槽建模

通过已建模的螺旋槽截面，根据螺旋运动的特点，可知立铣刀螺旋槽建模是由螺旋槽截面进行拉伸与旋转运动所形成，将立铣刀螺旋槽由平行于螺旋槽截面的平面进行切分，可知每一被平面截出的分段都都与切割平面呈螺旋角d的夹角，运用微积分方法，沿轴线把螺旋槽切分成无数个微小单元体，其各相邻单元体绕轴线都旋转固定角度，将这些单元体叠加起来的，即可完成螺旋槽的三维建模。

基于上述理论，需要求得每一单元体所旋转的角度，如图5所示为螺旋槽刃线分析视图，选取刀立铣刀刀头B1位置为螺旋线的起点位置，通过螺旋角d延A1B1螺旋刃线旋转到A1点螺旋槽终点位置，那么将螺旋槽展开成矩形，通过式(17)求得由B1点到A1点螺旋截面绕刀具轴线所旋转转的总角度v。

v=2L7·tan(u)/L1

(17)

再通过微积分的方法可以求出每个单元体所转的角度v1，将其每一单元体结合，便获取到整个螺旋槽所需要的点云信息。

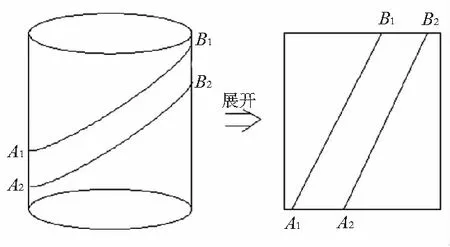
图5 螺旋槽展开

4 构建三角网格

由于在OpenGL中模型的绘制都是以三角面片为基本图元进行搭建的，所以需要将所求得的螺旋槽关键点以三角面片进行相连，其中如图3的螺旋槽截面，可将所有的关键点与截面中心点O1进行连接直接构建出螺旋槽截面的三角网格；在螺旋槽网格化中，由于螺旋槽是柱状形体，可将螺旋槽简化为圆柱体，把螺旋槽的每个分段以圆柱体的分段连接作为参考，然而在螺旋槽的建模中，需要考虑到每个单元体都是在上一个单元体的基础上经过一定的角度旋转后得到，那么在螺旋槽的关键点连接中，由式(17)得到旋转的总角度，则每个单元体都在上个单元体基础上旋转了v1，则相邻俩个单元体的连接，如图6所示，T1是T2的上一个单元体，ω为旋转方向，通过关键点的索引信息构建三角形，即俩个三角形Δ0′1′1，Δ1′12模板，将所有的相邻单元体关键点按照索引Δ0′1′1，Δ1′12模板进行连接，即可完成螺旋槽部分网格建模如图7所示。

图6 相邻单元体连接

图7 螺旋槽网格建模

5 立铣刀参数化建模系统的应用

利用vs2015可视化编程工具进行OpenGL绘制，将所得螺旋槽三角网格进行OpenGL渲染，添加光照、材质等渲染参数。

并通过MFC设计合理的参数输入、参数显示以及绘制的操作界面，构建完整的参数化建模系统，以某型号硬质合金圆柱立铣刀进行参数化建模，其参数如表2所示。

表2 立铣刀螺旋槽面截面相关参数与数值

依次设置参数完毕后，如图8所示，点击“计算模型”生成立铣刀螺旋槽的三维模型，如图9所示。

图8 系统参数输入

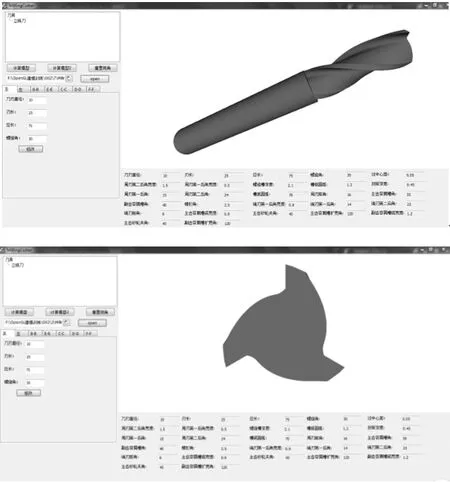
图9 系统运行结果

不同螺旋槽槽深(1.8mm，2.4mm)的模型如图10所示。

(a)1.8mm螺旋槽截面 (b)2.4mm螺旋槽截面图10 螺旋槽截面对比

6 结束语

本文通过详细分析立铣刀螺旋槽的结构特点，以面向立铣刀工程图进行立铣刀螺旋槽特征设计，研究商业建模软件的建模原理，提出了关键点建模的方法，建立了立铣刀螺旋槽的数学模型，并完成模型的三角网格化，在Visual Studio2015平台上，将模型网格进行OpenGL渲染，搭建出立铣刀螺旋槽三维参数化建模系统。建模实例证明该系统能够精确的完成立铣刀螺旋槽的三维参数化建模，系统运行稳定可靠，操作方便快捷，并具有独立的技术体系，可以实现刀具的设计与制造的市场推广与相关的研究扩展，并为类似的机械设计建模提供了参考。

[参考文献]

[1] 米蓉. 立铣刀三维参数化设计系统研发[D]. 成都：西南交通大学，2011.

[2] 赵鑫,卓勇,展慧娴,等.整体硬质合金刀具参数化直接建模的研究与实现[J].机电工程,2014,31(6):725-728.

[3] 熊烽,宾鸿赞.复杂形状刀具设计的三维可视化[J].工具技术,2002(4):18-21.

[4] 李宏德.立铣刀优化设计[J].制造技术与机床,2007(5):25-27.

[5] 夏文胜,赵先锋,高飞,等.锥度球头立铣刀磨削加工数学模型研究[J].组合机床与自动化加工技术,2016(1):122-126.

[6] 赵先锋.立铣刀螺旋槽数学模型及刀具切削性能仿真分析[D]. 贵州:贵州大学, 2013.

[7] 董元平,璩柏青,张洁,等. 运用逆向工程方法与OpenGL创建三维曲面[J]. 计算机仿真, 2007,24(9):168-171.

[8] 晏海平, 吴禄慎, 陈华伟. 基于VC和OpenGL的三维点云处理软件系统设计[J]. 计算机应用与软件, 2014, 31(6):177-180.

[9] 王兰美, 赵继成, 秦华东. OpenGL及其在VC++下的开发应用[C]. 中国工程图学学会2006年计算机图学、理论图学等专委会综合学术会议, 2006.

[10] 王兰美, 赵继成, 秦华东. OpenGL及其在VC++下的开发应用[J]. 武汉大学学报(工学版), 2006, 39(4):62-65.

[11] 刘建宁,李占锋,李大鹏.整体立铣刀参数化建模分析与研究[J].现代制造工程,2015(1):90-93.

[12] Tandon P, rajik K M.Three dimensional modeling and finiteelement simulation of a generic End mill [J].Computer aided design, 2009,41 (2):106-114.

[13] Kim, J H, park J W, Ko t j.End mill design and machiningvia cutting simulation [J].Computer aided design, 2008,40 (3):324-333.