在主动测量中的基于支持向量机尺寸判定的研究*

职占新，郑 鹏，田雪豪

(郑州大学 机械工程学院，郑州 450001)

0 引言

随着现代制造业的发展，人们对精密零器件加工过程的控制与检测的高精度、智能化要求越来越高。磨加工主动测量仪是一种能够实时检测工件尺寸[1-4]，通过测量值与设定信号点值的比较判断，对机床发出动作指令进而控制磨削加工进程的仪器。广泛应用于自动、半自动磨床，可有效提高产品质量的一致性，降低废品率[5]。然而实际磨削加工过程中，在主动测量仪控制下的工件往往由于圆度误差等影响，加工后的实际尺寸与预设值之间存在偏差。目前在国内的实际生产过程中，解决这一问题的办法主要是试验加工小批量的工件，通过测量尺寸，手动设置补调值来修正由于圆度误差引起的偏差。但在不同批次、大批量的流水线生产过程中依然无法满足自动化的要求。

为了提高量仪的自动化水平和工件的加工精度。解决由于圆度误差所引起的工件实际尺寸和量仪预设值有偏差的问题，提出了圆度误差修正尺寸判定方法，其中圆度误差是基于最小二乘支持向量机算法根据已有加工参数进行预测而获得的，能够让磨床在加工过程中不停机自动修正尺寸预设值，极大提高了自动化程度和降低工人劳动强度。

1 信号点到尺寸判定

磨加工时，一般采用“粗磨—精磨—光磨”的三级加工模式，如图1所示。

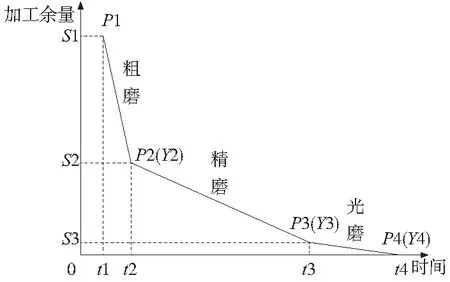
图1 磨加工主动量仪“粗磨—精磨—光磨”模式

图1中，P1、P2、P3、P4为加工信号预设点，S1—S2为粗磨阶段，S2—S3为精磨阶段，S3—S4为光磨阶段。当主动量仪测头检测到工件尺寸到信号预设点，控制系统发出信号，指导机床工作，控制砂轮进给速度。但实际加工过程中，由于圆度误差的存在，使得测头测得值存在偏差，导致加工工件尺寸与预设值存在偏差，比如外圆磨削的过程中，加工工件尺寸常常大于预设值尺寸。

在大批量的生产过程中，无法对每一个工件的每一个磨削阶段进行修正磨削补调值。所以结合了支持向量机算法提出了圆度误差修正尺寸判定方法。设到尺寸时工件圆度误差为Y，信号点预设值为D，则修正后的信号点预设值为：

D′=D-Y/2 (外圆磨削时)

D′=D+Y/2 (内圆磨削时)

2 最小二乘支持向量机的回归预测

2.1 最小二乘支持向量机

最小二乘支持向量机算法是由Suykens提出的，该算法在了经验风险最小的前提下，尽量保证置信风险变小。并且根据转换，显著的降低了运算的复杂程度，令运算速度提升，存储空间减少。

最小二乘向量机回归讨论，假设给定S个数据的训练集合：

{(x1,y1),(x2,y2)…(xi,yi)..(xs,ys)}，其中xi是多维的输入值，yi是输出值。i=1,2…s

对于最小二乘支持向量机来说，映射函数与一般支持向量机算法相同，将数据从原始空间映射到高维空间：

φ(x)={φ(x1),φ(x2),…,φ(xs)}

(1)

决策函数为：

f(x)=wT·φ(x)+b

(2)

其中，w为权重向量，b为误差常量。

结构风险R为：

(3)

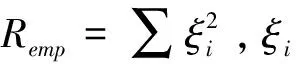
对模型参数的求解等效为以下优化问题的求解：

(4)

通过拉格朗日因子，与KKT算式，得出以下算式：

(5)

则支持向量机模型确定为：

(6)

式中，k(xi,xj)是核函数，本文采用RBF核函数。

2.2 交叉验证参数寻优

预测模型的建立只是回归分析的第一步，参数的优劣直接决定了模型性能的优劣，本文采用交叉验证的寻优方法来优化惩罚参数c，核参数g。

交叉验证是一种基于统计分析的寻优方法，可以有效的避免过学习和欠学习状态的发生，通过交叉验证往往可以得出比随机选取参数更为理想的准确率。

交叉验证较为常用的方法是K-fold CV，将实验数据分为K组，其中K-1组数据用来训练，剩余的一组用来验证模型准确率，每个子集都会用来验证模型优劣。这样会得到K个模型，并将K个模型的准确率做算术平均差，作为K-fold CV下的性能指标，因为每个实验组都参与了参数的选择，所以不存在由于分组导致结果不准确，最后得到的结果相比于其他的交叉验证方法比较有说服力。图2为通过Matlab2014的交叉验证寻优过程，坐标轴分别代表了不同的惩罚参数与核参数。当模型准确率相等或者近似相等时，我们优先选择惩罚参数c最小的那一组，因为当惩罚函数c升高的时候，训练集的分类准确率会相应的降低，即模型的泛化能力较弱。所以认为当模型准确率相近时，优先选择c较小的参数组作为最小二乘支持向量机的参数。

图2 交叉验证后的参数分布图

2.3 支持向量机算法预测模型

磨加工时两种工艺参数(砂轮进给速度，磨削余量)对工件圆度误差有较大影响，因此基于LSSVM建立圆度误差预测模型，根据这两种参数对工件的圆度误差进行预测，并且将通过模型得到的圆度误差与实际误差进行比对，最终确定实际模型，具体步骤如下：

对磨加工中的工件反复试验，通过改变磨削加工参数(砂轮进给速度，磨削余量)来获得不同的圆度误差。加工完成后将工件用最小区域法(MIC)来进行相关计算，最终得到工件的圆度误差。

选定训练集和测试集，并将选定的数据进行预处理，首先将数据中粗大误差提出，然后对训练集与测试集进行归一化处理，归一化函数如下：

f:x→y=(x-xmin)/xmax-xmin

其中，

x,y∈Rn,xmin=min(x),xmax=max(x)。该归一函数是将原始数据归一到[0,1]区间内，防止因为x过大影响归一效果。除了将原始数据归一到[0,1]区间，还可以将原始数据归一到[1,-1]区间内，归一函数如下：

f:x→y=2(x-xmin)/xmax-xmin+(-1)

通过训练集建立回归模型，并且通过交叉验证寻 找最佳参数(c,g)。然后将模型预测出的圆度误差yi与实际的圆度误差做对比。如果圆度误差预测值的误差在预设范围内，证明模型可行。

3 实验分析

实验采用外圆磨削的方式，选用的磨床型号为MGB1320E高精度半自动外圆磨床。采用GYSyn 256C磨削液；砂轮材质为棕刚玉，直径400mm,厚度32mm，最高线速度35m/s；如图3所示。

图3 磨削实验设备

在磨加工过程中，尽量避免对工件的过多接触，防止由于人为因素使实验结果有误差。在进行圆度误差评定的时候选取最小区域法(MIC)。采用MATLAB模拟，采用CV参数优化以后，得到最优参数(c=2.21,g=2.88)。磨削圆度误差试验结果与预测值表1所示。预测值与实际测量值对比如图4所示。

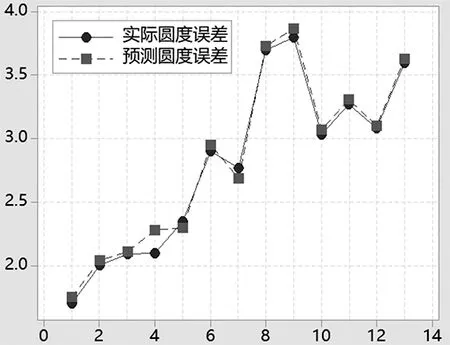
图4 圆度误差预测值与实测值对比

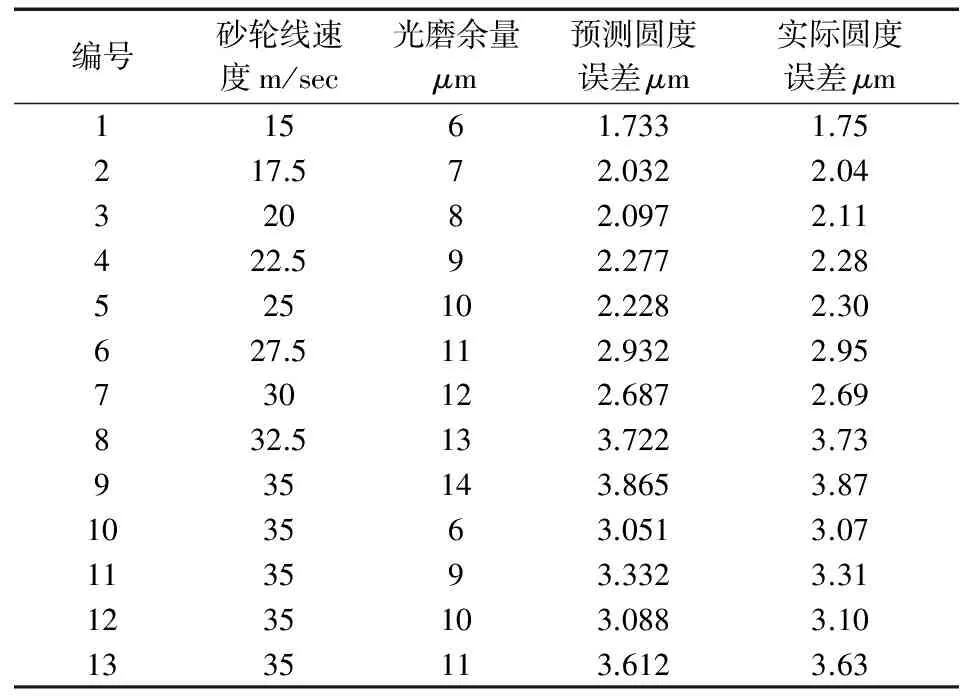
表1 磨削圆度误差试验结果与预测值

通过MATLAB运算得出模型样本平均相对误差与均方误差为MRE=0.0090,MSE=0.0050。模型的MRE与MSE越小越可靠，对数据的预测越精确，实验结果证明了模型的可行性。通过量仪将模型预测所得到的圆度误差来修正信号点预设值，设到尺寸时工件圆度误差为Y，信号点预设值为D，则修正后的信号点预设值为：

D′=D-Y/2 (外圆磨削时)

D′=D+Y/2 (内圆磨削时)

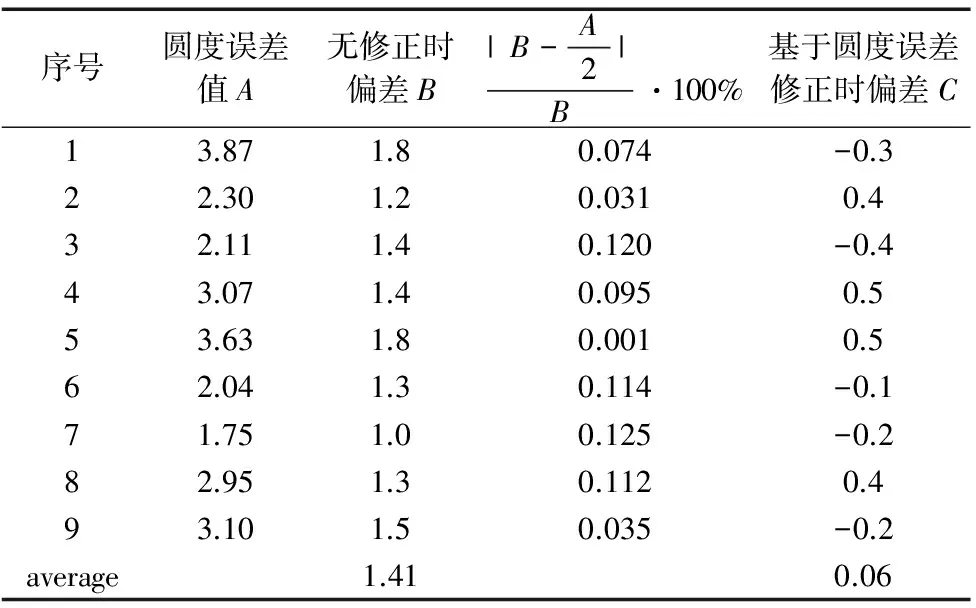
表2 实验结果

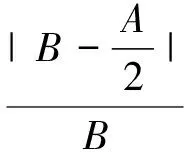
4 结论

通过对尺寸判定存在偏差的问题分析，提出了基于支持向量机的圆度误差修正的尺寸判定方法。通过最小二乘法支持向量机基础理论和交叉验证参数寻优搭建预测模型，提出将预测的圆度误差与信号预设值结合的修正方法。通过实验分析，将修正后的偏差与未修正的偏差做对比，提出的修正方法有效的降低了实际尺寸与预设值的偏差。并且采用了基于支持向量机的预测模型，对预设值实现自动补调，使得磨加工自动化程度进一步提升。研究成果对提升磨削过程自动化的水平有重要的意义。

[参考文献]

[1] 高方.磨加工主动测量控制的关键技术及应用[D].郑州：郑州大学,2014.

[2] 宁会峰.珩磨加工中在线气动测量与尺寸控制技术研究[D].兰州：兰州理工大学,2012.

[3] 任冠青,张琳娜，郑鹏.WinCE多线程在磨加工主动量仪控制系统中的应用[J].组合机床与自动化加工技术,2013(8):77-79.

[4] 陈六三,张兴权,汪世益,等. CBN砂轮磨削深度对渗碳淬火钢表面质量的影响[J]. 金属热处理,2013(6):89-92.

[5] 李国发,王龙山,丁宁. 基于进化神经网络外圆纵向磨削表面粗糙度的在线预测[J]. 中国机械工程,2005,16(3):223-226.

[6] 王家忠,王龙山,周桂红,等. 基于模糊基函数网络和自适应最小二乘算法的外圆纵向磨削表面粗糙度的预测[J]. 中国机械工程,2006,17(12):1223-1227.

[7] 牛家洋.基于神经网络的非线性系统时间序列的预测方法研究[D].济南:山东师范大学,2013.

[8]崔立志.灰色预测技术及其应用研究[D].南京:南京航空航天大学,2010.

[9] 向昌盛.基于支持向量机的时间序列组合预测模型[D].长沙:湖南农业大学,2011.

[10] 向红军,雷彬.基于单片机系统的数字滤波方法的研究[J].电测与仪表,2005(9):53-55.