中心典型形状开口的矩形薄板自由振动特性分析
2018-04-18张俊李天匀朱翔郭文杰陈繁
张俊 ,李天匀 ,朱翔 ,郭文杰 ,陈繁
1华中科技大学船舶与海洋工程学院,湖北武汉430074
2船舶与海洋水动力湖北省重点实验室,湖北武汉430074
3高新船舶与深海开发装备协同创新中心,上海200240
0 引 言
开口结构具有很多优势,其可以在保证一定强度的前提下减轻结构重量,还可以用于各种特殊的用途,使用范围非常广泛,尤其在船舶领域,如集装箱船的大开口结构、散货船的货仓开口、船体主体部分的人孔、排水孔以及上层建筑的结构开口等。但同时开口也会影响结构的强度、稳定性以及振动特性等性能,因此对开口结构进行研究具有重要意义。
近百年来,国内外的专家学者们对开口结构进行了大量研究,各种成果层出不穷。Cho等[1]应用假定振型法,通过运动的拉格朗日方程导出自然频率,对任意边界条件下开口板的自由振动特性进行研究,分析了开口大小对板结构动力响应的影响。Lu等[2]在带有2个孔的平板的应力解析解中对带有1个椭圆孔和1个圆孔的平板提出了解析解,并采用复变函数的方法将求解区域映射成了一个圆环,原区域求解的应力分布是这个圆环的特殊条件。同时,还具体介绍了映射函数、应力边界条件的复数表示法等。Kumari等[3]同样应用复变函数的方法,通过算例分析了带有不同大小孔的平板的应力分布。Jafari等[4]针对不同形状、不同大小开口矩形板的应力问题进行了求解,并针对不同形状、不同大小开口矩形板的应力分布给出了关系图像,其采用的也是复变函数解析方法。除此之外,Rayleigh-Ritz法也被用于求解带开口和裂纹的结构问题。邱永康等[5]和王旻昊等[6]在任意边界条件下中心开矩形口矩形板的自由振动特性分析和基于傅立叶级数法的含开口板的振动固有特性分析中,对开矩形口的矩形板的问题进行了系统分析,讨论了开口位置、开口大小等对矩形板自由振动特性的影响。李凯等[7]在基于能量泛函的开口矩形板自由振动特性分析中,采用区域分解及能量泛函的方法计算了开口矩形板的自由振动频率,得出了振型。
本文将基于Rayleigh-Ritz法,对任意边界条件下典型形状开口矩形薄板进行分析。首先,采用改进的傅里叶级数法[8-11]模拟求解域的位移容许函数,解决以往函数边界不连续的问题;为求解复杂边界条件下的结构自由振动,采用线性分布的位移约束弹簧和转角约束弹簧,通过改变弹簧的刚度系数模拟各种经典边界条件。然后,通过算例说明方法良好的收敛性和精确性。最后,对比文献[5-7]中对矩形板开矩形口的区域划分方法,本文将采取不将整块板划分为若干个小矩形板块的方法,而是直接对整个求解域进行求解,以较准确地计算诸如圆形开口、椭圆形开口这种带有曲边的开口形状,大大减少计算量,从而为之后计算任意形状开口问题提供可能。
1 理论分析
1.1 开口矩形板的物理模型
本文研究的物理模型为中心开圆形、椭圆形开口的矩形薄板,如图1所示。开口矩形板的长为a,宽为b,板厚为h,圆形、椭圆形(其长轴与短轴和矩形边界平行)开口的中心与矩形板中心重合。
为了方便计算任意边界条件下开口矩形板的自由振动固有频率,本文采用沿边界均匀分布的位移约束弹簧k和转角约束弹簧K,通过改变两类弹簧的刚度系数来简便、快捷地模拟各种任意边界条件。各种经典的边界条件及对应的弹簧刚度系数如表1所示。

表1 经典边界条件下的弹簧刚度系数Table 1 Values of spring stiffness of classical boundary conditions
根据以上弹簧模拟任意边界条件的方法,可得到开口矩形薄板的物理模型如图2所示。
由于本文的研究对象具有高度的对称性,为简化计算,只研究1/4的结构,通过对称性的正对称和反对称的性质来得出整体开口矩形板的固有频率。本文研究对象的计算模型如图3所示。
本文选取改进的傅里叶级数方法来作为开口矩形板的位移容许函数,可表示为[11]:
式中:Amn为未知傅里叶级数展开系数;简谐时间因子eiωt表示开口矩形板垂向位移与时间相关的项;M,N为截断项数;ϕm(x)为x方向的容许梁函数;ψn(y)为y方向的容许梁函数。
根据改进的傅里叶级数方法,式(1)中的ϕm(x)与ψn(y)可分别表示为:
式中:m=1,2,3,…,M;n=1,2,3,…,N。
1.2 含开口板的自由振动能量分析
本文基于Rayleigh-Ritz法,首先求得结构整体的能量方程,然后再针对傅里叶级数展开中的未知系数求极值,将问题转化为求解标准特征值的问题。下面,将以开圆口的矩形薄板为例进行分析。
未开口板结构的弯曲应变能为:
开口部分结构的弯曲应变能为:
未开口矩形薄板的动能可以表示为:
开口部分的动能可以表示为:
式中,ρ为材料的密度。
储存在边界约束弹簧中的弹簧势能为
式中:kx0,ky0,kxa,kyb分别为x=0,y=0,x=a/2,y=b/2处位移约束弹簧的刚度值;Kx0,Ky0,Kxa,Kyb分别为x=0,y=0,x=a/2,y=b/2处转角约束弹簧的刚度值;R为开口半径。
于是,整体结构的能量泛函即可表示为[12]
对未知的傅里叶级数展开求极值,可得
这样,就可以将自由振动的问题转化成求特征值的问题,简化计算。具体可以表示为
式中:K=Ks+Kp,其中Ks为弹簧能量的刚度矩阵,Kp为整体结构应变能的刚度矩阵;M为结构的质量矩阵;A为未知的Fourier系数向量;ω为圆频率。
2 数值计算与分析
本文对复杂边界条件下典型形状开口矩形板的自由振动特性进行分析计算,比较不同开口大小和不同开口形状对开口板固有频率的影响,并与有限元软件ANSYS的计算结果进行对比,分析说明本文方法的精确性。选用钢材,材料的参数取值取为:材料密度ρ=7 850 kg/m3,泊松比μ=0.3,材料的杨氏模量E=2.1×1011Pa。将开圆口的矩形薄板作为收敛性分析的研究对象。
2.1 收敛性分析
上文的分析表明,位移容许函数中的截断项数M,N的取值对结果的精度影响很大。在模拟边界条件时,刚度系数可能需要取∞,由于应用Matlab进行数值计算时弹簧的刚度系数只能取一个有限的、具体的值,故刚度系数的取值对结果的影响也很大。本次收敛性分析主要是针对以上2个量进行。首先,对截断项数M,N的取值进行收敛性分析。选取四边自由(F-F-F-F)的开圆口的矩形板作为研究对象,相关几何参数如下:矩形板长a=6 m,宽 b=4 m,厚度 h=0.02 m,内开口半径R=1 m。计算其前6阶的固有频率值(单位:Hz),为便于分析,这里取M=N(表2)。

表2 四边自由(F-F-F-F)边界条件下开圆口矩形板的固有频率Table 2 Natural frequencies of rectangular plate with a circular opening in F-F-F-F boundary
分析表2中的数据可知:随着截断项数M,N的不断增加,圆形开口矩形薄板的固有频率逐渐趋于稳定,当M=N=12时,固有频率已基本不再发生变化。可以认为,当截断项数取12时采用本文的方法已经收敛,证明了改进傅里叶级数方法在计算开口板振动特性方面的收敛性。表中计算数据与有限元软件计算结果相差很小,证明了计算的精确性。后面的计算中将均取截断项M=N=12。
然后,对弹簧的刚度系数取值进行收敛性分析。选取固支(C-C-C-C)边界条件下开圆口的矩形板作为研究对象,相关几何参数如下:矩形板长a=6 m,宽b=4 m,厚度h=0.02 m,内开口半径R=1 m,计算其前6阶的固有频率值。根据表2的分析,这里取截断项数M=N=12,分析不同弹簧刚度系数下(K=k=10r)的计算结果,结果如表3所示。

表3 M=N=12时固支(C-C-C-C)边界条件下开圆口矩形板的固有频率Table 3 Natural frequencies of rectangular plate with a circularopening in C-C-C-C boundary(M=N=12)
表3中的数据表明:随着弹簧刚度系数值的不断增加,圆形开口矩形薄板的固有频率逐渐趋于稳定,当指数r=14时,固有频率已基本不再发生变化,可以认为当弹簧刚度指数r=14时即可代替某些弹簧刚度系数取无穷的情况,例如简支时位移弹簧的刚度系数、固支时位移弹簧和转角弹簧的刚度系数等,且取得的结果较为精确,具有良好的收敛性和准确性。该计算数据与有限元软件计算结果吻合较好。所以在后面计算中,将取弹簧刚度系数k=1014N/m,K=1014(N·m)/rad来代替取∞时模拟的简支、固支边界。
2.2 准确性分析
下面对本文方法的准确性进行分析。选取固支边界条件下开圆口的矩形板和简支(S-S-S-S)边界条件下开椭圆口的矩形板作为研究对象,相关几何参数如下:矩形板长a=6 m,宽b=4 m,厚度h=0.02 m,开口半径R=1 m,椭圆长半轴短半轴,计算其前6阶的固有频率值。为便于分析,这里取M=N,并与有限元软件计算结果进行了对比,结果如表4和表5所示。

表4 固支边界条件下开圆口矩形板的固有频率对比Table 4 Comparison ofnatural frequencies of rectangular plate with a circular opening in C-C-C-C boundary

表5 简支(S-S-S-S)条件下开椭圆口矩形板的固有频率对比Table 5 Comparison ofnatural frequencies of rectangular plate with an ellipse opening in S-S-S-S boundary
提取前4阶固有频率的模态振型图,并与有限元仿真软件(ANSYS)振型图进行对比,如图4所示。图4中,每个分图中的上图为采用本文方法所得振型,下图为有限元方法所得振型。图4表明计算所得振型与有限元方法所得振型基本一致,证明了本文方法的正确性。
选取固支边界条件下开圆口矩形板为研究对象,计算不同大小开口下开口板的自由振动频率。相关几何参数如下:矩形板长a=6 m,宽b=4 m,厚度h=0.02 m,计算开口半径R=0(无开口),0.5,0.75,1.0,1.25,1.5 m时,其前6阶的固有频率值。为便于分析,取M=N。与有限元软件计算结果的对比如表6所示。

表6 固支边界条件下开不同面积圆口矩形板的固有频率Table 6 Natural frequencies of rectangular plate with different areas of circular opening in C-C-C-C boundary
2.3 开口尺寸对开口板自由振动性能的影响分析
开口尺寸对开口板自由振动特性有着最为直接的影响,利用本文方法,通过对不同开口面积开口板的自由振动固有频率进行计算分析,总结了开口板的自由振动特性与开口面积的定性关系。
研究开口尺寸对开口板振动特性的影响。在固支边界条件下,研究开圆口矩形薄板的自由振动特性。矩形板长a=6 m,宽b=4 m,厚度h=0.02 m,设开口中心与板的中心重合,为开口半径分别为R=0(无开口),0.5,0.75,1.0,1.25,1.5 m的圆形,对比分析开口板前6阶的固有频率值。
为了更加直观地得到简支、固支条件下开口矩形板的自由振动特性规律,将计算数据绘制成如图5、图6所示。
从图5中可以看出,对于第1阶固有频率,在固支条件下,随着开口面积的增大,自由振动固有频率也增大,但其对高阶自由振动固有频率的影响并不明显。对于上述现象可能的解释如下:固有频率与结构刚度和质量都有关系。在板的中心开口不仅会降低结构的刚度,也会降低结构的质量,而对于简支和固支边界条件下的矩形板,其第1阶振型的形状极为相似,均是中心部分具有较大的位移,所以在板中心开口会使结构质量降低得更加迅速,从而导致其整体频率呈上升趋势。但对于其他阶的频率,因其振型不一定是中心的位移较大,所以在中心开口结构的质量不一定会降低得更多,故固有频率也就不一定呈上升趋势。
通过对比图5和图6可以看出,对于简支和固支边界条件,开口大小对固有频率的影响趋势基本一致,这可能是因为在简支和固支条件下,开口矩形板的振型类似,因而有上述现象。
2.4 开口形状对开口板自由振动性能影响分析
最后讨论开口形状对开口板自由振动特性的影响。在固支边界条件下,矩形薄板长a=6 m,宽b=4 m,厚度h=0.02 m,内开口面积S=π m2,对比矩形薄板开矩形、圆形、椭圆形口时前3阶固有频率的变化,提取前3阶固有频率计算结果如表7所示。
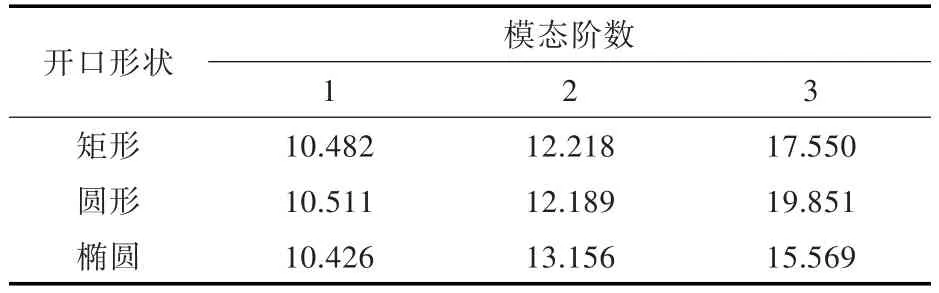
表7 固支边界条件下不同开口形状开口板的固有频率Table 7 Natural frequenciesofrectangularplatewith different shaped openings in C-C-C-C boundary
为了更加直观地表示开口形状对固有频率的影响,将计算数据绘制成了如图7所示的图像。
由图7可以看出,对于第1阶固有频率,当开口面积相同时,自由振动的第1阶固有频率几乎没变化,因而可以得出结论:当开口很小时,开口板自由振动的第1阶固有频率值与形状基本无关。而高阶的固有频率与开口形状则有一定的关系。对于上述现象的解释如下:对于固支边界条件,第1阶振型的形变主要集中在中心部分,而本文研究的是中心开口的矩形薄板,中心变形大的地方均被开口截掉了,而边缘部分的影响则不大,所以刚度变化、质量变化对不同形状的开口来说几乎相同。文献[6]的研究也表明,对于不同的开口位置来说,开口越靠近中心部分,开口板的首阶固有频率就越小,这也可以作为上述解释的证明。
3 结 语
本文基于Rayleigh-Ritz法,将开口矩形板的自由振动问题转化为了求特征值的问题,通过采用改进的傅里叶级数方法模拟位移容许函数,应用沿边界线性分布的位移约束弹簧和转角约束弹簧模拟各种任意边界条件,研究了典型开口形状矩形薄板的自由振动特性。通过典型的算例,将所得频率和振型结果与有限元模拟给出的频率、振型结果进行了对比,证明了本方法的收敛性和准确性。同时,还探讨了不同开口大小和开口形状对开口矩形薄板自由振动的影响,通过结合趋势图与振型图,得出开口对结构自由振动固有频率的影响与对应频率阶数的振型有关,在某阶频率所对应振型振幅较大处,开口将更加显著地增加该阶的固有频率。
参考文献:
[1]CHO D S,VLADIMIR N,CHOI T M.Approximate nat⁃ural vibration analysis of rectangular plates with open⁃ings using assumed mode method[J].International Journal of Naval Architecture and Ocean Engineering,2013,5(3):478-491.
[2]LU A Z,XU Z,ZHANG N.Stress analytical solution for an infinite plane containing two holes[J].Interna⁃tional Journal of Mechanical Sciences,2017,128/129:224-234.
[3]KUMARI S,UPHADHYAY A K,SHUKLA K K.Stress analysis for an infinite plate with circular holes[C]//5th International Conference on Materials Processing and Characterization(ICMPC 2016),2016.
[4]JAFARI M,ARDALANI E.Stress concentration in fi⁃nite metallic plates with regular holes[J].Internation⁃alJournalofMechanicalSciences,2016,106:220-230.
[5]邱永康,李天匀,朱翔,等.任意边界条件下中心开口矩形板自由振动特性分析[J].振动与冲击,2017,36(20):112-117.QIU Y K,LI T Y,ZHU X,et al.The free vibration char⁃acteristics analysis of rectangular plate with central opening using in arbitrary boundary conditions[J].Journal of Vibration and Shock,2017,36(20):112-117(in Chinese).
[6]王旻昊,李凯,邱永康,等.基于傅里叶级数法的开孔板振动固有特性分析[J].中国舰船研究,2017,12(4):102-109.WANG M H,LI K,QIU Y K,et al.Free vibration char⁃acteristics analysis of rectangular plate with rectangu⁃lar opening based on Fourier series method[J].Chi⁃nese Journal of Ship Research,2017,12(4):102-109(in Chinese).
[7]李凯,何书韬,吴国民,等.基于能量泛函的开口矩形板自由振动特性分析[J].振动与冲击,2017,36(11):161-165.LI K,HE S T,WU G M,et al.The free vibration char⁃acteristics analysis of rectangular plate with central opening using energy functional method[J].Journal of Vibration and Shock,2017,36(11):161-165(in Chi⁃nese).
[8]LI W L.Free vibrations of beams with general bound⁃ary conditions[J].Journal of Sound and Vibration,2000,237(4):709-725.
[9]LI W L.Vibration analysis of rectangular plates with general elastic boundary supports[J]. Journal of Sound and Vibration,2004,273(3):619-635.
[10]LI W L,ZHANG X F,DU J T,et al.An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports[J].Journal of Sound and Vibration,2009,321(1/2):254-269.
[11]王青山,史冬岩,罗祥程.任意边界条件下矩形板的面内自由振动特性[J].华南理工大学学报(自然科学版),2015,43(6):127-134.WANG Q S,SHI D Y,LUO X C.In-plane free vibra⁃tion of rectangular plates in arbitrary boundary condi⁃tions[J].Journal of South China University of Tech⁃nology(Natural Science Edition),2015,43(6):127-134(in Chinese).
[12]TAKAHASHI S.Vibration of rectangular plates with circular holes[J].Bulletin of JSME,1958,1(4):380-385.
