一种基于粒子群算法的生产线缓冲区容量分配技术

刘军马超

（兰州理工大学机电工程学院　兰州　730050）

1　引言

缓冲区容量优化分配问题（Buffer Allocation Problem，BAP）是一个NP-hard组合优化问题，也是设计制造系统中一个重要的研究方向。缓冲区容量分配问题是在生产线系统中找到最优的缓冲区容量配置从而完成特定的目标，根据目标的不同，可以将该问题分为三类：缓冲区总量一定时，以最大化生产率为目标对缓冲区容量进行分配；生产线生产率一定时，以最小化缓冲区总量为目标对缓冲区容量进行分配；缓冲区总量和生产线生产率一定时，以生产线上平均在制品数量最少为目标对缓冲区进行分配。自1959年Koenigsberg［1］首次研究该问题以来，各国学者在该领域已进行了逾50年的探索。主要通过两步循环迭代法，即利用有关解生成方法进行容量分配，然后利用生产线性能近似分析技术进行性能评价，反复迭代直至获得缓冲区容量分配最优解。其中，解生成方法的发展尤为突出。最简单的生成方法就是Chow的遍历空间法［2］，但只适用于小型系统，当设备数和缓冲区容量增加时可行解数量呈指数增长无法搜索到整个解空间。早期传统搜索方法，如分支定界法［3］、梯度法［4］等作为解生成方法在缓冲区容量分配问题中得到广泛应用，但其主要缺陷是易于陷入局部最优，同时难以观察缓冲区容量微小变化对生产线系统性能造成的影响。因此近年来随着人工智能、计算机技术的发展，研究者应用元启发式算法解决缓冲区容量分配问题。Nahas［5］利用遗传算法作为解生成方法很好地解决了生产率一定总花费最小目标条件下的问题。ZhouBinghai［6］将蚁群算法用于解决生产率最大目标函数下的缓冲区分配问题较DC算法、GA算法表现出更快的收敛速度和更好的精度。为更好地搜索解空间，将元启发式算法与其它方法混合使用也成为主要的技术发展趋势之一。Kose［7］提出一种遗传模拟退火算法解决直线型生产线缓冲区分配问题，较单纯遗传算法、模拟退火算法具有更快的搜索速度和更好的搜索结果。Mohtashami［8］提出的基于线性搜索的混合遗传算法在解决最小花费和最大生产率目标条件下的缓冲区分配问题时，表现出较好的搜索性能。

粒子群算法（particle swarm optimization，PSO）作为新一代群智能元启发式算法，自1995年被James Kennedy和Russell Eberhart等［9］提出后，由于其概念简单，调整参数较少，易于编程，没有复杂的数学操作，对计算机硬件的速度和存储要求不高等特性，引起了许多学者的兴趣和重视。但是由于粒子群算法出现的历史较短，该算法用于解决BAP问题的研究尚不多，在理论基础和应用上还有一些急待解决的问题。2002年Elgallad和Fgee等用神经网络改进粒子群算法第一次将其用于缓冲区分配问题［10］。2009年Can和Heavey将遗传算法和粒子群算法相结合用于解决直线型生产线缓冲区容量分配问题，该方法对离散变量空间搜索时表现出较高的精度［11］。2014年 Narasimhamu和 Reddy等用平均值近似分析法作为评价算法，粒子群算法作为解生成算法，解决具有单一服务器的串行闭环排队网络模型［12］。2014年Phatak用PSO算法很好地解决了装配线缓冲区容量分配问题［13］。但是上述研究都没有克服粒子群算法局部搜索能力差以及早熟收敛的缺点。

基于此，针对受随机故障等随机事件影响的直线型生产线系统，提出一种多种群粒子群分析技术，解决生产线在缓冲区总量固定、生产率最大的目标条件下的缓冲区容量优化分配技术问题。该技术将一定规模的粒子群平分成多个种群，分别按照ω线性递减策略的粒子群算法的规则进化，并对各种群中粒子群算法附以不同的惯性权重，通过“移民算子”实现各种群的协同进化，并将各种群每代的最优个体放入精华种群加以保存。既保持各子群进化的独立性，又保证子群间进化的合作性。在同样的实验参数设置下，本文方法与传统经典粒子群改进算法进行比较。结果表明，该技术用于小型、大型生产线系统较传统算法具有收敛精度高、鲁棒性好、局部搜索能力强等优点，可以在较小的迭代次数内搜索到全局最优解，对克服早熟收敛有显著效果，是对当前缓冲区分配问题研究领域解生成技术的一个有效补充。

2　问题描述

本文所研究的受随机故障等随机事件影响的直线型生产线由 K台设备(M1⋅⋅⋅Mk)，K-1个缓冲区 (B1⋅⋅⋅Bk-1)串联组成，如图1所示。

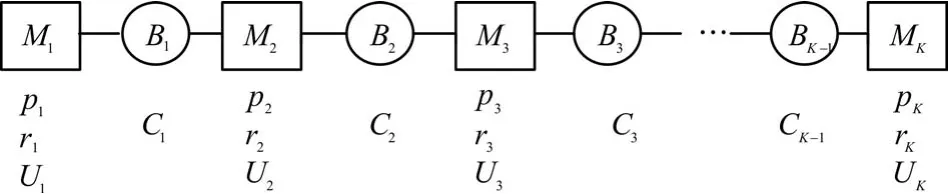
图1　直线型生产线模型

原材料从生产线外部进入，在第一台设备M1进行加工，再进入第一个缓冲区B1，并依次经过后面各个设备和缓冲区，直到最后一台设备Mk，最终离开该生产线。Ci为生产线中各个缓冲区的最大缓冲区容量，在任意时间t时，缓冲区Bi中产品总量为ni∈[0，Ci]，假设如下：

1）每台设备具有正常工作与故障维修两种状态。令 αi∈{0，1} 表示设备状态，i=1，2，…，K 为设备。αi=1表示正常运行状态，若αi=0则表示故障维修状态。

2）Mi上游相邻设备发生故障时，此设备与Mi之间的缓冲区中的原材料数量趋于减少，当缓冲区为空时，设备Mi出现“饥饿”现象。Mi下游相邻设备发生故障时，此设备与设备Mi之间缓冲区中的原材料数量趋于增加，当缓冲区充满时，设备Mi处于“阻塞”状态。

3）假定设备故障为依靠操作型故障，即设备仅在操作时发生故障而与时间无关。当设备既不出现“饥饿”又不出现“阻塞”且正常运行时，其处于工作状态。当设备Mi正常工作时，产品以连续生产率U从上游缓冲区Bi-1流向下游缓冲区Bi，且其满足Ui=1/Ti，Ti为设备加工时间。

4）假设M1不存在“饥饿”现象，而Mk不存在“堵塞”现象。当设备工作时，令 pi为设备故障率，且服从指数分布，则1 pi表示两故障之间的平均工作时间。令ri为设备维修率，且服从指数分布，则设备的平均维修时间记为1 ri，假设当发生故障时，产品在设备中，经维修，得以恢复正常时，生产加工仍然继续进行。

现令 f(ni)为生产线的平均生产率，N为生产线的缓冲区总量，解决直线型生产线在缓冲区总量固定、生产率最大的目标条件下的缓冲区容量分配技术问题。目标函数如下所示：

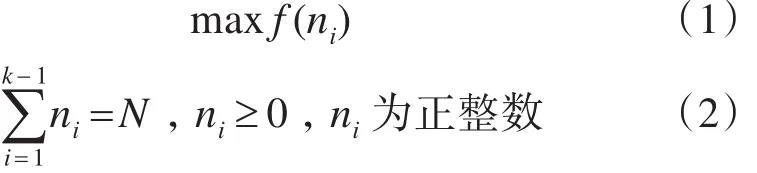
其中，ni(i=1⋅⋅⋅k-1)为正整数，代表为使生产率最大各个缓冲区需要配置的缓冲区容量；f(ni)为各个缓冲区容量为ni时整条生产线的生产率；N代表生产线的缓冲区总量，取值为正整数。这里需要注意的是：

生产线平均生产率由设备数K、每个设备的平均工作效率Ui、故障率 pi、维修率ri、分布类型以及各个缓冲区分配的容量ni所决定。本文先用分解法对生产线进行评价从而得到平均生产率，然后利用多种群粒子群分析技术作为解生成方法进行容量分配，反复迭代直至获得缓冲区容量分配最优解。如图2所示。

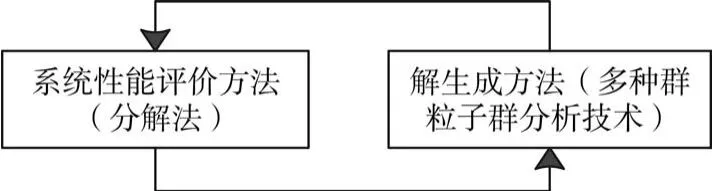
图2　解决BAP问题的方法

3　分解方法

分解方法基本思想是引入虚拟设备，将K台设备组成的生产线L，分解成K-1条由上游设备Mu(i)和下游设备Md(i)构成的双设备生产线L(i)(i=1，2，3，⋅⋅⋅，k-1)通过反复迭代，不断调整虚拟设备的参数使各双设备生产线L(i)具有原始生产线的操作特性而最终获得原系统的操作性能指标。具体详细的过程参照文献［14］。

以如图3所示的三台设备生产线L为例，引入虚拟设备Mu(i)和Md(i)，将原生产线分解为子生产线L(i-2)和L(i-1)。分解后设备Mu(i-2)，Md(i-1)的参数保持为原设备参数值不变，通过往复式迭代求解虚拟设备Md(i-2)和Mu(i-1)的设备性能参数以保持原生产线操作特性为目标，最终获得系统性能指标。

图3　分解方法示例

4　多种群粒子群分析技术

4.1　粒子群算法

粒子群算法首先在可行解空间中初始化一群粒子，每个粒子都代表极值优化问题的一个潜在最优解，用位置、速度和适应度三项指标表示该粒子特征，适应度值由适应度函数计算得到，其值的好坏表示粒子的优劣。粒子在解空间中运动，通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。粒子每更新一次位置，就计算一次适应度值，并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值和群体极值位置。其数学模型为：在D维目标搜索解空间中，有n个粒子组成一个种群 X=(X1，X2，…，Xn)。 Xi=(Xi1，Xi2，…，Xin)代表第i个粒子的位置，也表示一个潜在的最优解。每个粒子的速度用Vi=(Vi1，Vi2，…，ViD)表示。个体极值Pbest为第i个微粒所经历过的具有最好适应值的位置，记为 Pi=(Pi1，Pi2，…，PiD)；群体极值Gbest为整个微粒群所经历过的最好位置，记为 Pg=(Pg1，Pg2，…，PgD)。根据目标函数可以得出粒子位置对应的适应度值，以适应度值大小衡量粒子的优劣。粒子群中各个粒子的位置和速度不断的进化，其进化方程为

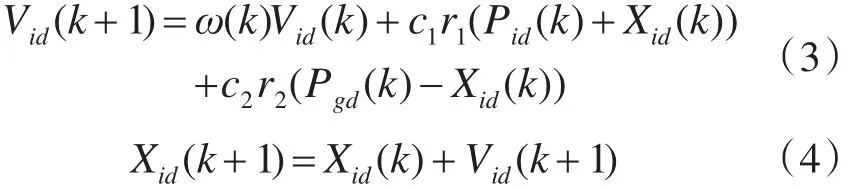
其中，i=1，2，…，n为粒子数；d=1，2，…，D 为维数；k为当前迭代次数；Xid第i个粒子第d维的位置；Vid为第i个粒子第d维的速度；Pid为个体极值；Pgd为群体极值；ω为惯性权重值；r1和r2为[0 ， 1]之间随机数；c1和c2为加速度因子，是非负的常数。为防止粒子盲目的搜索，一般将速度限制在一定的范围[-Vmax，Vmax] 。

在式（3）中，第一项为粒子当前速度的影响，第二项为粒子个体最好位置的影响，第三项为群体最好位置的影响。第一项用来平衡全局和局部搜索能力；第二项反映粒子自身经验的影响，使粒子具有全局搜索能力，避免陷入局部极值；第三项反映群体经验的影响，体现了粒子间的信息共享。

4.2　多种群粒子群分析技术

多种群粒子群分析技术（multiple population Particle Swarm Optimization，MPPSO）的基本思想是将一定规模的粒子群平分成多个种群，分别按照ω线性递减策略的粒子群算法的规则进化，对各种群中粒子群算法附以不同的惯性权重，并在每一次迭代结束后进行比较，从而得出相对于三个种群最优个体的最优个体，放入精华种群保存起来。既保持独立性一面，即每一个子群按照不同的算法规则计算；又有合作性的一面，即通过“移民算子”实现各种群的协同进化。

4.2.1多种群的算法

多种群粒子群分析技术突破传统粒子群算法仅靠单个群体进行搜索的框架，将一定规模的种群平分成多个子群，分别按照粒子群算法的规则进行优化搜索。各子群中的粒子群取不同的参数，同时进行搜索，极大地增加了种群的多样性，避免早熟收敛的发生，更快更好地搜索到整个解空间。

多种群是相对独立的，相互之间通过“移民算子”联系。“移民算子”将各子群在进化过程中出现的最优个体定期地引入其他子群中，实现种群之间的信息交换。具体的操作规则是，将目标种群的最差个体用源种群的最优个体代替。“移民算子”在多种群粒子群算法中至关重要，如果没有“移民算子”，各种群之间就失去了联系，将等同于用不同的控制参数进行多次粒子群计算，从而失去了多种群的特色。

在进化的每一代结束后对各个种群进行比较，从而得出相对于多个种群最优个体的最优个体。“精华种群保留算子”将最优个体放入精华种群加以保存，保证进化过程中各种群产生的最优个体不被破坏和丢失。

4.2.2ω的线性递减策略

多种群粒子群分析技术各子群均按照ω线性递减策略的粒子群算法的规则进化。ω是可变参数，如果ω取值较大，则全局搜索能力强，局部搜索能力弱，不易得到精确解；如果ω较小，则局部搜索能力强，全局搜索能力弱，粒子在局部徘徊，收敛速度慢且会陷入局部“最优解”。为了使算法的全局搜索能力和局部搜索能力得到均衡，我们对ω进行线性递减的改进，如式（5）所示。初期较大的ω使算法具有较强的搜索能力，而后期较小的ω又能够得到相对精确的结果，从而提高了算法的性能。

式（5）中的ωstart为初始惯性权重，ωend为迭代至最大迭代次数时的惯性权重，k为当前的迭代次数，T为最大的迭代次数。

为了使得各子群的参数不同，ωstart服从[0.70-0.95]的均匀分布，ωend服从[0.3-0.45]的均匀分布。通过多个采用线性递减策略且惯性权重不同的种群协同进化，很大程度上增大了种群的多样性，避免早熟收敛的发生，使得算法更快更精确地搜索到最优解。如下所示：

4.3　多种群粒子群分析技术的流程

1）确定种群规模且平分为M个种群进行位置和速度的初始化，设置相关参数。

2）将分解法作为适应度函数分别对各种群中的粒子进行评价，得出适应度值，记录各种群的个体最优和群体最优。

3）根据式（5～6）计算出 ω ，再由式（3～4）对粒子的速度和位置进行更新。

4）计算各种群中各个粒子的适应度值，用各种群的最优适应度值更新个体最优与群体最优。

5）对控制参数不同的M个种群进行移民操作，将目标种群的最差个体用源种群的最优个体代替。

6）在进化的每一代，将所有种群的最优个体放入精华种群加以保存。

7）如果达到终止条件则停止，否则转到步骤2）。

5　仿真实验

仿真环境：主频为2.4GHz，i5-2430的双核英特尔第二代酷睿处理器（L700-T33B型号的东芝计算机）、W in7旗舰版32位系统以及Matlab R2011b软件。

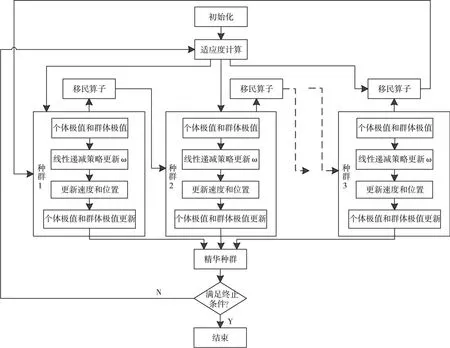
图4　多种群粒子群分析技术的流程图

为了验证算法的有效性，针对常用五设备小型串行生产线和二十设备大型串行生产线分别利用本文提出的多种群粒子群分析技术（MPPSO）、标准粒子群算法（WPSO）［15］与随机惯性权重粒子群算法（MPSO）［15］的实验数据进行了比较。在实验中，假设每台设备连续工作时间和出现故障后的修复时间都满足指数分布，其平均正常工作时间（MTTF）和平均修复时间（MTTR）已经给定。

参数设置：种群规模sizepop=20，学习因子c1=c2=0.5。WPSO算法的ω=0.9，MPSO算法的ωmax=0.9，ωmin=0.4。所有算法迭代次数100，每个实验设置运行100次，将100次的平均值作为最终结果。五设备生产线的缓冲区总量B=31。二十设备生产线中，用于分配的总缓存容量B=100，其余参数设置如表1所示。

表1　五设备生产线的设备参数

表2　三种算法下五设备生产线的生产效率

表3　二十设备生产线的设备参数

表4　三种算法下二十设备生产线的缓冲区配置

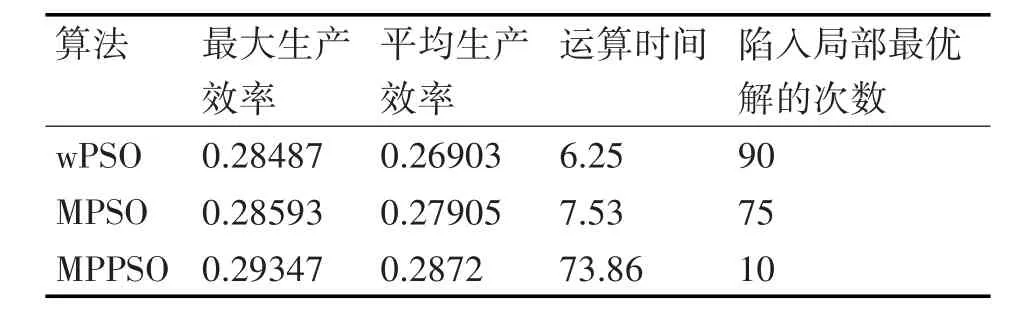
表5　三种算法下二十设备生产线的生产效率

由表2、表4、表5可以看出对于五设备小型生产线MPPSO的最大生产效率、平均生产效率略高于WPSO和MPSO，对于二十设备大型生产线MPPSO的最大生产效率、平均生产效率远远优于其他两种算法。两种生产线中MPPSO陷入局部最优次数均远高于其他两种算法，然而MPPSO的运行时间均多于其他算法。

结合以上数值实验分析可知，随着生产线复杂程度的增加，MPPSO的收敛精度和鲁棒性较其他两种算法更优，可以在较小的迭代次数内寻找到最优解，更容易跳出局部最优，搜索到全局最优解，避免早熟收敛，然而需要的运算时间较长。

当群体规模较小时，群体多样性程度低，个体之间竞争性较弱，随着进化的进行，群体很快趋于单一化，比较容易陷入局部最优，造成早熟收敛。然而群体规模过大将会导致计算时间大幅增加，计算效率受到影响，并且当群体数目增长至一定水平时，再增长将不再有显著的作用。MPPSO将一定规模的种群平分成多个子群，分别按照粒子群算法的规则进行优化搜索，通过增加种群个数来提高种群规模，并利用“移民算子”进行联系，将各子群在进化过程中出现的最优个体定期地引入其他的种群中，实现种群之间的信息交换，互相联系，协同进化，大大增加了种群的多样性，很好地避免了早熟收敛的发生。然而种群规模的扩大必然导致计算时间的增加，在后期学习中将致力于减少运算时间的研究中。

较大的惯性权重将使粒子具有较大的速度，从而有较强的全局搜索能力；较小的惯性权重将使粒子具有较强的局部搜索能力。惯性权重的恰当设定涉及粒子群算法全局搜索和局部搜索能力的均衡，进化搜索的最终结果对惯性权重的取值相当敏感，不同的值很可能会导致不同的计算结果。传统粒子群算法采用经验值惯性权重，极易造成早熟收敛的发生。本文提出的算法对各种群取不同的惯性权重，并且对惯性权重进行了线性递减的改进，各种群前期ω变化相对较慢，取值较大，使得算法的全局收敛能力增强；后期ω变化相对较快，极大地提高了局部寻优能力，种群间协调进化，同时兼顾了算法的全局搜索和局部搜索能力，使得算法更快更精确地搜索到最优解，很好地避免了早熟收敛的发生。

6　结语

针对受随机故障等随机事件影响的直线型生产线系统，提出一种多种群粒子群分析技术，解决生产线在缓冲区总量固定、生产率最大的目标条件下的缓冲区容量优化分配技术问题。该技术将一定规模的粒子群平分成多个种群，分别按照ω线性递减策略的粒子群算法的规则进化，并对各种群中粒子群算法附以不同的惯性权重，通过“移民算子”实现各种群的协同进化，并将各种群每代的最优个体放入精华种群加以保存。既保持各子群进化的独立性，又保证子群间进化的合作性。在同样的实验参数设置下，本文方法与传统经典粒子群改进算法在小型、大型生产线系统中进行比较。结果表明，随着生产线复杂程度的增加，该技术较传统算法具有收敛精度高、鲁棒性好、局部搜索能力强等优点，可以在较小的迭代次数内搜索到全局最优解，对克服早熟收敛有显著效果。然而需要较长的运算时间，如何提高收敛速度，降低运算时间将会是今后研究中值得考虑的问题。另外，本文研究的主要模型为直线型生产线，但在实际生产中还有许多其他类型更加复杂的生产线比如平行线、装配线、环线。希望在以后的研究中将本文的方法进行扩展，可以在更多类型生产线上得到应用。

［1］Koenigsberg，E.Production lines and internal storage—A review［J］.ManagementScience，2007，59（5）：410-433.

［2］Chow W M.Buffer Capacity Analysis for Sequential Production Lines With Variable Process Times.［J］.International Journal of Production Research，1987，25（8）：1183-1196.

［3］DolguiA，Eremeev A V.HBBA：hybrid algorithm for buffer allocation in tandem production lines［J］.Journalof IntelligentManufacturing，2007，18（3）：411-420.

［4］Gershwin S B，Schor JE.Efficient algorithms for buffer space allocation［J］.Annals of Operations Research，2000，93（1）：117-144.

［5］Nahas N.Bufferallocation，machine selection and preventive maintenance optimization in unreliable production lines［J］.Journal of IntelligentManufacturing，2014，209（1）：1-9.

［6］ZhouBinghai，YuJiadi.Buffer allocation method of serial production lines based on improve dantcolony optimization algorithm［J］.高技术通讯（英文版），2016，22（2）：113-119.

［7］Kose SY，Kilincci O.Hybrid approach for buffer allocation in open serial production lines［J］.Computers&Operations Research，2015，60（C）：67-78.

［8］Köse SY，Demir L，TunalıS，et al.Capacity improvement using simulation optimization approaches：A case study in the thermotechnology industry［J］.Engineering Optimization，2014，47（2）：1-16.

［9］Kennedy J，Eberhart R.Particle swarm optimization［C］//IEEEInternational Conference onNeural Networks，1995.Proceedings.IEEE，1995：1942-1948 vol.4.

［10］Elgallad A，El-Hawary M，Phillips W，et al.PSO-based neural network for dynamic bandwidth re-allocation［power system communication］［C］//Power Engineering 2002 Large Engineering Systems Conference on，LESCOPE 02.IEEE，2002：98-102.

［11］Can B，Heavey C.Sequentialmetamodelling with genetic programming and particle swarms［C］//Simulation Conference.IEEE，2009：3150-3157.

［12］Narasimhamu K L，Reddy V V，Rao CSP.Optimal Buffer Allocation in Tandem Closed Queuing Network with Single Server Using PSO ☆［J］.Procedia Materials Science，2014，5：2084-2089.

［13］Phatak S，Venkateswaran J，Pandey G，etal.Simulation based optimization using PSO in manufacturing flow problems：a case study［C］//SimulationConference.IEEE，2014：2136-2146.

［14］Liu J，Kong J，Fan Q.Performance Analysis of Non-Homogeneous Hybrid Production Lines［J］.2014，4（5）：463-467.

［15］张志宇，白云霞.粒子群算法不同惯性权重之间的比较［J］.淮海工学院学报：自然科学版，2016，25（1）：1-6.WANG Zhiyu，BAIYunxia.Comparison ofDifferent Inertia Weight Based on Particle Swarm Optimization［J］.Journal of Huaihai Institute of Technology：Natural Science Edition，2016，25（1）：1-6.