一种新的联合跳频信号参数估计算法

张志宝　孙微涛　罗文峰　张　力

（中国人民解放军63788部队　渭南　714000）

1　引言

跳频通信具有隐蔽性强、截获难度大、抗干扰性强、保密性好等优点，因此被广泛应用于航天测控、雷达技术、卫星导航和现代通信等各个领域，现已成为电子对抗环境下提高通信抗干扰能力最有效的措施［1］。跳频信号参数估计是截获对方通信信号，提高自身通信对抗能力的首要前提，在现代军事通信对抗中有着重要的现实意义［2］。近年来，为了解决跳频信号的时频分析和参数估计，许多学者提出了大量算法，陈超等［3］基于 WVD（Wigner-Ville）分布提出了改进的参数估计算法，该算法具有较高的时频分辨率，但是由于频率变化的非线性致使存在严重的交叉项干扰。张曦等［4］根据小波变换多分辨率的特点提出了跳频信号参数估计算法，该算法在高频段频率分辨率低，不适合频率估计精度要求较高场合。刘玉珍等［5］采用平滑伪Wigner-Ville分布对跳频信号的参数进行估计，该算法在时域和频域的平滑，从而减少了交叉项的干扰，但是降低了时频分辨率，运算量大幅增加。STFT是时频分析中一种典型的线性变换，该方法没有交叉项干扰，能有效估计出参数，具有较强抗噪能力。

根据不确定性原理［6］，针对STFT在跳频信号参数估计中，不能同时兼顾时间分辨率和频率分辨率的不足，本文提出一种新的联合跳频信号参数估计算法，即对跳频信号进行STFT变换，提取其时频脊线，得到跳变时刻的精确估计，然后提取两个跳变时刻之间的信号对其进行AR（Auto Regressive）谱分析，得到跳频频率的精确估计。

2　STFT算法和AR谱估计原理

2.1　STTF算法

短时傅里叶变换（STFT）是一种最常用的时频分析方法，其本质就是加入窗函数后的傅里叶变换。STFT的基本思想：将一个窗函数与所要研究的连续时间信号相乘，然后对其进行傅里叶变换，信号频率随时间的变化规律就可以通过在时间轴上移动窗函数来实现［7］。其定义如下

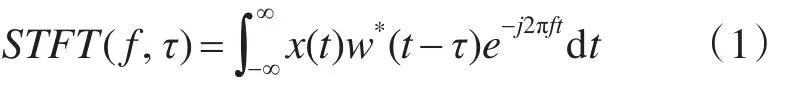
式中*代表复数共轭，w(t)为窗函数。由此可得到连续时间信号x(t)在τ时刻的短时傅里叶变换，就是将连续信号x(t)与一个以t为中心的窗函数w*(t-τ)相乘，然后对其进行傅里叶变换。STFT的时间分辨率和频率分辨率与窗函数的选取有直接的关系，若在相同窗函数下，窗长越长，频率分辨率越高，时间分辨率越低。

2.2　AR谱估计

AR模型，又称为自回归模型，是一种全极点模型［8］。AR谱估计是现代功率谱估计中最常用的一种方法，该方法具有计算简单，谱估计精度高和系统稳定等优点，因此被广泛应用于故障诊断、图像处理、目标识别等领域。AR模型参数估计算法主要有自相关法、Burg算法和改进协方差算法［9～10］。Burg算法是根据序列数据进行推导出的，该算法在考虑数据段两边的未知数据的同时还要使预测误差滤波器的相位最小，具有较好的频率分辨率［11］。

AR算法的基本思想：首先根据被分析序列的前向和后向预测误差的平均功率最小准则估计出反射系数，然后再利用Levinson递推求得AR模型的参数［12］。定义线性预测误差格型滤波器的前向误差为eb(n)，后向误差为ef(n)，利用前向和后向预测误差的平均功率最小准则，求出满足条件的反射系数，再按Levinson递推计算AR模型参数{ap(1)，ap(2)，…，ap(p)， Pp=σ2} ，已知n)=n)=x(n)递推公式如下

3　联合参数估计算法

跳频信号的一般形式可表示为

式中：A为信号幅度，fj和θj为在 jT≤t＜(j+1)T时第 j个跳频信号分量的频率和相位，w(t)为高斯白噪声。

理论上各跳频时隙的持续时间相等，即所得各峰值间的间隔应该是相等的，但受STFT估计误差的影响，实际测得的各时隙持续时间不完全相等，并且经常相差很大。由于各时隙持续时间总是在真实值处的一个范围内波动，所以可将差分曲线上的峰值点选取出来，利用最小二乘法作线性拟合得出一条直线，该直线的斜率和跳频速率紧密相关。

选取 K 个峰值点位置 p(i)，i=1，2，3，…，K ，把其转换成(xi，yi)的坐标形式，其中xi=i，代表时隙数编号；yi=p(i)，代表细估计时得到的跳变时刻。将这K个坐标点代入最小二乘法的公式（6～8）即可确定该直线。

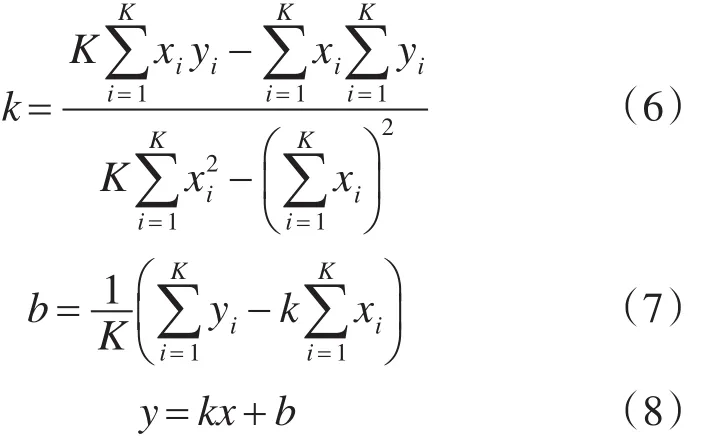
该直线的斜率就是跳频周期。利用该拟合直线在各xi点处的值可进一步修正跳变时刻。

图1是联合参数估计算法的流程图，具体实现步骤如下

1）首先对 x(n)进行短时傅里叶变换，选取4N0+1点的矩形窗（N0为正整数），且每次滑动N0点，得到 X0(n，k)。

2）提取 X0(n，k)的频率脊线，即计算 X0(n，k)中每个时间点沿频率轴最大幅度所对应的频率点，得到TF(n)。

3）对TF(n)进行差分运算法，求出各差分序列最大值对应的采样点ni，估计出了各跳变时刻=ni⋅Ts(i=1，2，…，K)。且跳频周期得估计值为

图1　跳频信号参数估计流程图

4　仿真及结果分析

设跳频信号的参数为：A=1，SNR=5dB，跳速为2000hops/s，频点间隔Δf=25kHz。共15个跳频频率点，f1=25kHz ，取跳频序列为 fi={f1，f2，f4，f8，f3，f6，f12，f11} 。跳变时刻 ti=｛0.5，1，1.5，2，2.5，3，3.5｝。得到的跳频信号及跳频图案如图2所示。

按照第3节算法步骤对上述仿仿真信号进行参数估计，结果如图3所示。

其中，图 3（a）是由 ti步骤 1）求得的信号时频图，从图中可以看出STFT时频图具有较好的时间分辨率。图3（b）是由步骤2）求得的时频脊线图，图中跳频信号的时频特性较为明显。图3（c）是经差分运算得到的峰值序列。图4是对粗略估计的跳变时刻进行最小二乘拟合，由此计算修正后的跳变时刻。

图2　仿真跳频信号及其跳频图案

图3　粗估计时的时频图、频率脊线及其差分

图4　跳变时刻的最小二乘拟合

表1给出了SNR=5dB时，500次统计独立试验各跳频频点起始跳变时刻ti的估计结果。由表中数据可以得出，该算法对各个跳频频点起始时刻进行估计，所得到的估计值与真实值之间相差无几，平均相对误差小于0.1%。另外由表1给出的跳变时刻计算或由图4跳频周期的平均值Th=0.50012ms，估计的相对误差仅为0.023%。

表1　500次统计独立试验各跳频频点起始跳变时刻估计值 单位：ms

表2给出了各跳频频点起始跳变时刻ti修正前与修正后的估计值，由表中的数据可知，采用最小二乘拟合后跳变时刻估计的误差及方差性能都有明显改善。

表2　采用最小二乘法修正跳变时刻前后的估计值对比　单位：ms

表3给500次统计独立试验各跳频频率 f的估计结果。由表中数据可以得出，该算法对各个跳频频率进行估计，所得到的估计值与真实值之间相差无几，平均相对误差小于0.4%。

表3　500次统计独立试验各跳频频率的估计值单位：KHz

5　结语

本文基于STFT和AR谱估计中的Burg算法，提出了一种新的联合跳频信号参数估计算法。本文首先对算法原理进行了详细分析，然后给出了跳频信号参数估计的具体步骤，最后通过仿真实验证明了该算法对跳频信号参数估计的可行性和有效性。另外本文还针对估计得到的各时隙持续时间可能不完全相等情况，在前期估计的基础上利用最小二乘拟合修正跳变时刻的估计值，有效地改善了跳变时刻的估计精度，并可得到跳频周期的估计值。

［1］梅文华.跳频通信［M］.北京：国防工业出版社，2005.MEI Wenhua.Frequency hopping communication［M］.Beijing：NationalDefend Industry Press，2005.

［2］Hlawatsch F，Auger F.Time-frequency analysis：Concepts and Methods［M］.London（UK）：ISTE andWiley，2008.

［3］陈超，郝雁中，高宪军，等.基于WVD改进算法的跳频信号参数估计［J］.吉林大学学报（信息科学版），2010，28（2）：124-130.CHEN Chao，HAO Yanzhong，GAO Xianjun，etal.Parameter estimation of frequency-hopping signals based on amelioration algorithm ofWVD［J］.Journalof Jilin University（Information Science Edition），2010，28（2）：124-130.

［4］张曦，王星，杜兴民.基于小波变换的跳频信号参数盲估计［J］.电路与系统学报，2009，1（4）：60-65.ZHANG Xi，WANG Xing，DU Xingmin.Blind parameter estimation of frequency-hopping signals based on wavelet transform［J］.Journal of Circuits and Systems，2009，1（4）：60-65.

［5］刘玉珍，赵冉.基于改进WVD的跳频信号参数估计方法［J］.计算机工程与设计，2011，32（11）：3916-3919.LIU Yuzhen，ZHAO Ran.Frequency-hopping signal parameter estimation based on improved WVD［J］.Computer Engineering and Design，2011，32（11）：3916-3919.

［6］Yingke L，Zifa Z，YanhuaW.A new hop duration blind estimation algorithm for frequency hopping signals［J］.Computational Intelligence and Industrial Application PACIIA，2008：695-699.

［7］张曦，杜兴民，茹乐.改进的快速短时傅里叶变换算法在跳频信号分析中的应用［J］.探测与控制学报，2007，29（2）：30-34.ZHANG Xi，DU Xingmin，RU Le.Application of amodified fast STFTmethod in frequency hopping signals analysis［J］.Journal of Detection&Control，2007，29（2）：30-34.

［8］闫庆华，程兆刚，段云龙.AR模型功率谱估计及Matlab实现［J］.计算机与数字工程，2010，38（4）：154-156.YAN Qinghua，CHENG Zhaogang，DUAN Yunlong.Power spectrum density estimation for AR model and the simulation in Matlab［J］.Computer&Digital Engineering，2010，38（4）：154-156.

［9］孙志强，陈延平.基于Burg法AR模型谱估计的涡街流量计旋涡脱落频率提取［J］.中南大学学报（自然科学版），2013，44（4）：1684-1688.SUN Zhiqiang，CHEN Yanping.Extraction of vortex flow meter frequency by Burg algorithm based AR model spectral estimation［J］.Journal of Central South University（Science and Technology），2013，44（4）：1684-1688.

［10］陈伟，邢依依，刘梦婷.一种基于Burg谱估计和FFT的频偏估计方法［J］.电子科技，2016，29（3）：160-163.CHENWei，XING Yiyi，LIU Mengting.A frequency offset estimation algorithm based on Burg spectrum estimation and FFT［J］.Electronic Science&Technology，2016，29（3）：160-163.

［11］张莉，康耀红，王曙光，等.Burg法AR谱估计图像滤波分析与实现［J］.海南大学学报（自然科学版），2004，22（4）：336-339.ZHANG Li，KANG Yaohong，WANG Shuguang，et al.Burg analysisand implementation ofautoregressivemodel［J］.Natural Science Journalof Hainan University，2004，22（4）：336-339.

［12］陈宇，陈怀海，李赞澄，等.基于时变AR模型和小波变换的时变参数识别［J］.国外电子测量技术，2011，30（7）：20-23.

CHEN Yu，CHEN Huaihai，LIZancheng，etal.Identification of time-varying parameters base on time-varying AR model and wavelet transform［J］.Foreign Electronic Measurement Technology，2011，30（7）：20-23.