基于SIFT特征点的点云配准方法

张少玉

（西安工程大学　西安　710048）

1　引言

随着经济的发展、人们生活水平的提高，三维模型被广泛应用于医疗、娱乐、教育等行业，由此带来三维建模技术的发展，但是由于当前技术的局限性，并不能获得完整的点云数据，每次只能获得某个角度的点云数据，因此就需要多方位地进行三维扫描，这就使得在建模之前必须先进行点云配准，即将不同视角下的点云变换到同一坐标系下，它是图像处理、虚拟现实、测绘工程等领域的一项关键技术，点云配准的精度和速度直接影响三维建模的精度和速度。

目前点云配准算法中，最常用的就是Besl［1］和Chen［2］等分别提出的迭代最近点（Iterative Closest Point，ICP）算法，该算法是通过两片点云的对应点不断迭代确定旋转和平移矩阵，直到满足收敛条件，但是使用该算法时，若两片点云的初始姿态不好，则会形成局部最小化，造成迭代不能收敛到正确的结果；而且对应点的选取速度较慢。因此为了克服ICP算法自身的部分缺陷，许多研究人员对其进行了改进，其中很多人把点云的刚性特征应用进来，对其改进。点云的刚性特征有曲率、点法向与邻域点法向的夹角、点法向、局部张量、点与邻域重心的距离等［3～4］。特征法首先提取点云的刚性特征，利用特征进行粗配准，然后使用特征改进的ICP算法进行精配准。戴静兰等［5］、Yang等［6］使用曲率特征进行配准，但是估计曲率时需要用到近邻点，就会受到噪声的影响，而且估计曲率需要消耗大量的时间。Jiang等［7］使用夹角特征进行配准，虽然其方法提高了点云配准的误差收敛速度，但是计算和比较点之间的K维夹角特征耗费了不少时间。RUSU等［8］提出了一种基于法矢量的特征直方图，根据法矢量建立局部坐标系，用邻近点的距离关系和法矢量夹角的直方图表示该点的特征，但是该方法受噪声干扰明显，而且计算量较大。

本文提出一种使用尺度不变特征转换（Scale Invariant Feature Transform，SIFT）特征点的改进方法。该方法的基本要求就是两片点云数据有足够的重合度。该方法直接使用求得的源点云的特征点与体素栅格下采样后的目标点云进行配准，减少了计算特征描述子的环节，从而提高了配准速度，并通过随机采样一致算法（Random Sample Consensus，RANSAC）去除错误匹配点对，来提高配准的精度。虽然王程冬等［9］也提出使用SIFT特征进行点云配准，但是其方法是在二维图像中进行SIFT特征检测，通过映射关系来获得三维对应特征点，而本文是直接在三维点云数据中进行SIFT特征点检测，避免了因为映射关系可能会找到错误对应特征点的可能，同时也大大减少了算法的运行时间。

2　相关理论

2.1　体素栅格下采样

由于获取的点云数据数量比较大，若是全部用来做实验，则会影响后续实验的速度，因此采用部分点云来代替所有的点云来提高速度。PCL中的VoxelGrid类便可实现此目的，其通过输入的点云数据创建一个三维体素栅格（可把体素栅格想象成微小的空间三维立方体的集合），然后在每个体素内用体素中所有点的重心来近似显示体素中其他点。步骤如下：

1）立方体边长 L 的确定［10～11］。 L 的确定非常关键，在L过大的情况下会降低搜索效率，如果L过小，则会出现很多空的栅格。小立方体栅格边长为：L=α3s c，其中，α是用来调节小立方体栅格的边长的比例因子，s是比例系数，c是小栅格中的点云数量。

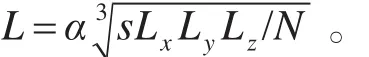
3）求得每个小栅格的重心实现下采样。每个栅格的重心为

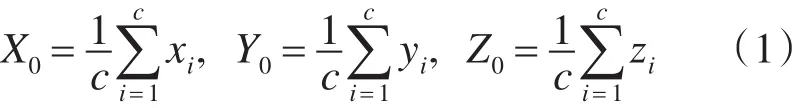
用(X0，Y0，Z0)代表该小栅格中的所有点，实现点云的下采样，达到精简点云数据的目的。

通过体素栅格下采样后，点云的数量减少了，但是点云的形状特征并未发生变化，因此在点配准之前通过此方法来提高配准速度。如图1所示，（a）为原点云数据，（b）为体素栅格下采样后的数据，可以看出点云的形状保持不变，只是显得稍微稀疏。

图1　体素栅格下采样结果

2.2　SIFT算法

SIFT算法［12］是Lowe DG提出的一种基于尺度空间的图像局部特征描述算法。虽然它只能描述图像的局部特征，但是该特征对视角变化、仿射变换、噪声保持一定的稳定性，对旋转、尺度缩放、亮度变化保持不变性，其原理如下：

1）尺度空间的生成

把原图像 I(x，y)与高斯核G(x，y，σ)的卷积定义为一幅图像的尺度空间L(x，y，σ)：

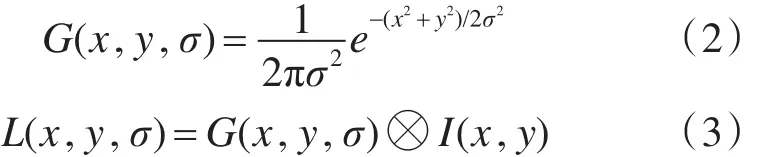
其中，G(x，y，σ)是尺度可变高斯函数，σ为尺度空间因子，其决定图像的平滑程度，(x，y)为图像像素坐标。

2）检测尺度空间极值点

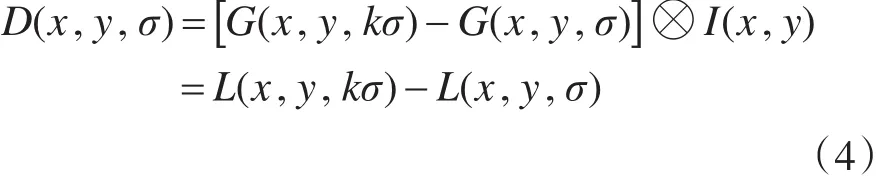
其中，D(x，y，σ)为高斯差分函数，引入该函数是为了有效检测出尺度空间中的稳定特征点，式（8）中，k为常量。在检测极值点时，每个像素点要与26个点（同尺度的相邻的8个像素点和其上下相邻尺度的9×2个点）进行比较，如果该像素点的DoG（Dif-ference ofGaussian）算子在这26个邻域中为最大或最小，则该点为特征点。

3）精确定位极值点

通过拟合三维二次函数以精确定位特征点的位置和尺度（达到亚像素精度），同时去除低对比度的特征点和不稳定的边缘响应点，以增强匹配稳定性，提高抗噪声能力。对尺度空间DoG函数进行曲线拟合，利用DoG函数在尺度空间的泰勒展开式：

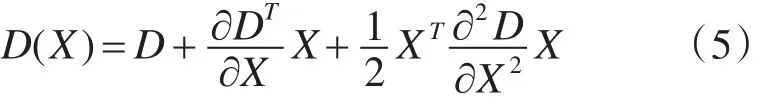
其中，向量 X=(x，y，σ)，对式（5）进行求导并使一阶导数为0，可得特征点精确位置的偏移向量：

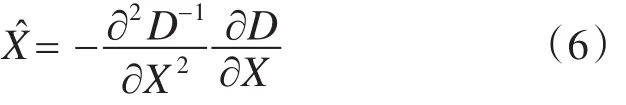
4）为每个特征点指定方向参数

利用特征点邻域像素的梯度方向分布特性为每个特征点指定方向参数，使算子具备旋转不变性。每个像素的梯度模和方向分别为

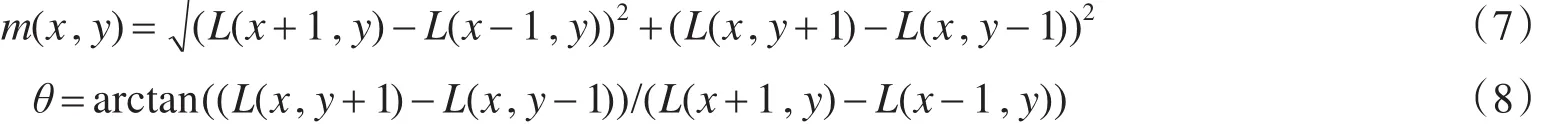
在以特征点为中心的邻域窗口内采样，并用直方图统计邻域像素的梯度方向。梯度直方图的范围是0°～360°，每10°为一柱，以梯度模 M作为贡献权重，即离中心点越远的邻域其对直方图的贡献就越小。

至此，图像的特征点已检测完毕，每个特征点有三个信息：位置、所处尺度和方向。如图2所示，是通过SIFT算法对两幅图像进行检测的结果。

图2　两幅图像SIFT特征检测结果

因此，PCL中的SIFTKpoint类将二维图像中的SIFT算子调整移植到了3D空间中，该类可以计算出点云的SIFT特征点，使SIFT算子实现了在3D空间中的直接应用。如图3所示，是在一片点云中求得SIFT特征点的结果，图中小圆点部分为人体上半身的点云数据，方形点就是检测出来的SIFT特征点。

图3　点云的SIFT特征点检测结果

2.3 RANSAC算法

RANSAC是一种随机参数估计方法，于1981年由 Fischler和Bolles［13］最先提出，主要思路是通过采样和验证的策略，求解大部分样本都能满足的数学模型参数。具体步骤为

针对应用需求，综合考虑各种通讯方式的传输带宽、覆盖范围、实时性、资费，最终选择采用GPRS/3G/卫星通信相结合的多模传输方式。主控制器的数据发送线程实现系统的多模数据发送功能，采用wvdial脚本和ppp脚本配置华为E261联通3G无线上网卡和SIM900A型GPRS模块连接网络[13]，卫星通信模块采用ORBCOMM公司的OG2卫星调制解调器，在3G和GPRS无网络的情况下系统自动切换至卫星通信模式，通过串口将定位和报警信息数据包发送给卫星通信模块，经卫星通信模块发送至服务器。

1）从样本集中选取4对匹配点作为内点集合，使用最小方差估计算法对这个集合计算模型参数；

2）用1）中得到的模型去测试所有的其它匹配点对，如果小于设定阈值，则加入内点集合；

3）如果迭代次数大于设定的阈值，则退出；否则重复步骤1）和2），选取内点个数最多的一组作为合格的匹配点集，并根据新的内点集合重新估计模型。

如图4所示，是RANSAC算法在二维数据集中的简单应用。图4（a）图既包含了局内点又包含了局外点，图4（b）中圆形为局内点，方形为局外点，直线就是基于RANSAC得到的适应数据的模型。

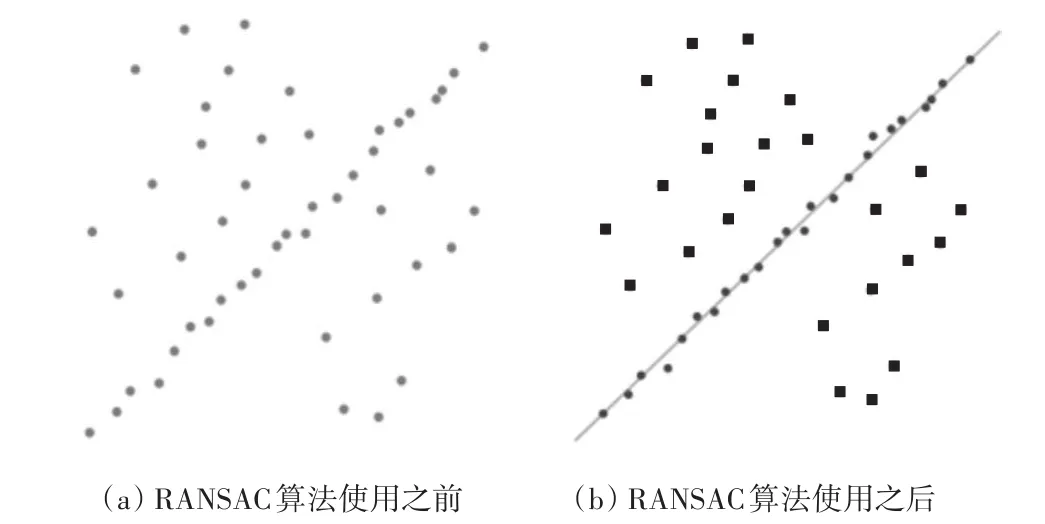
图4　RANSAC算法原理示意图

3　本文配准方法

3.1　ICP算法

ICP算法是一个经典的点云配准算法，它的基本原理是不断地寻找对应点集和求解变换关系，直到找到源点云和目标点云之间的旋转矩阵R和平移向量T，最终使源点云与目标点云满足某种条件下的最优匹配。

设源点云为 P={pi|pi∈R3，i=1，2，…，N} ，目标 点 云 为 Q={qj|qj∈R3，j=1，2，…，M} ，其 中N≤M。

步骤如下：

2）在目标点云Q中寻找源点云P每个点 pi的最近点pi'；

3）计算出源点云和目标点云的刚体变换矩阵R和T；

4）更新源点云P，计算得出P'=Rpi+T；

5）计算均方误差：

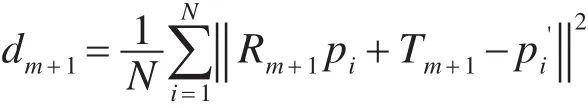
6）若dm-dm+1＜γ或者达到迭代次数，则停止迭代；否则反复执行2）～5）。

3.2　方法步骤

随着扫描技术的发展，获取的点云数量越来越大，这就对后期的处理带来不便，而经典的ICP算法计算效率不高，而且花费时间较多，因此本文提出一种改进方法。首先对两片点云进行体素栅格下采样，通过减少点云的数量来减少运行时间，其次用源点云的SIFT特征点与目标点云进行配准，并用RANSAC算法去除错误配对点，为了提高配准的精度，进行变换估计后，保留源点云，重复上述过程直到满足设定条件，步骤如下：

1）设定阈值λ＞0，用来判断程序是否终止；

2）对两片点云进行体素栅格下采样；

3）求取源点云的SIFT特征点。首先定义SIFT特征点检测；其次设置尺度相关参数，包括点云对应体素栅格中体素的最小尺寸，检测特征点时体素空间尺度的数目和为在每一个体素空间尺度下计算高斯空间的尺度时所需要的参数；然后设置候选特征点应有的对比度下限；最后输入点云，进行计算，对结果进行保存；

4）调用ICP算法，用保存的源点云SIFT特征点集与下采样后的目标点云进行配准；

5）采用RANSAC算法来剔除错误的匹配点对；

6）保留变换后的源点云，重复2）～5），若欧氏适合度评分（源点云到目标点云对应点对的距离平方和）（其中n为对应点对的数目，和是一对对应点中的两个点）小于给定的阈值λ，则一直重复2）～5），否则退出。

本文方法流程图如图5所示。

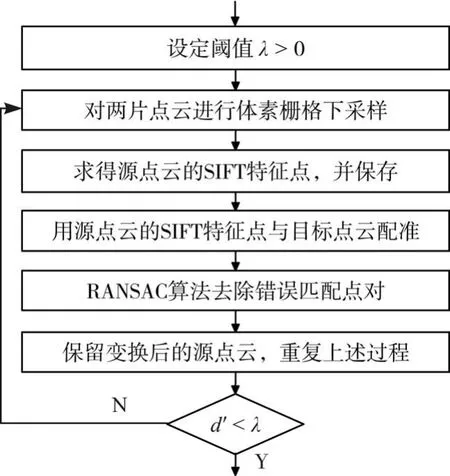
图5　本文方法流程图

4　实验结果与分析

本文用Kinect采集到的人体数据来验证本文方法的有效性。在图6中，（a）为采集到的两片点云数据，红色为目标点云，绿色为源点云，（b）为直接采用ICP算法进行配准的结果，可以看到（b）图中的源点云与（a）中稍有移动，但是不太明显，使得配准后的两片点云并没有成功融合在一起；（c）为采用本文方法提取的源点云的SIFT特征点，与原数据相比点云数量减少了很多，（d）为采用本文方法配准的结果，可以看到两片点云成功配准，与（b）相比效果良好。

图6　实验结果

表1是ICP算法与本文方法在时间和精度上的比较，可以看到本文方法在时间上比ICP算法减少了，欧氏适合度评分也比ICP算法小，因此本文方法取得了令人满意的效果。

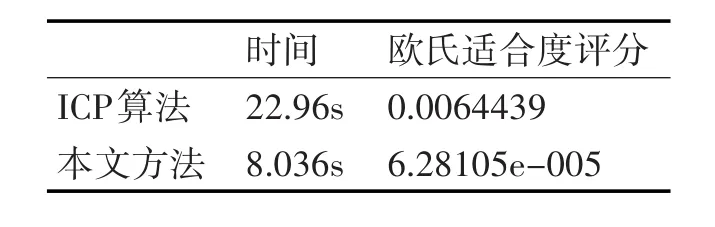
表1　ICP算法与本文方法比较

5　结语

针对ICP算法迭代耗时、精度较差的问题，本文提出结合SIFT特征点的方法对其进行改进。首先求出源点云的SIFT特征点，然后用该特征点集与目标点云进行配准，并通过RANSAC算法去除错误匹配点对，然后保留变换后的源点云进行重复，满足设定条件后退出程序。经实验表明本文方法得到了较好的配准精度和收敛速度。在实际应用中，有较高的使用价值。但是对于SIFT特征不明显的点云，配准效果较差，这也是本文下一步的研究方向。

［1］Besl P J，Mckay N D.A method for registration of 3D shapes［J］.IEEE Transactionson Pattern Analysisand Machine Intelligence，1992，14（2）：239-256.

［2］Chen Y，Medioni G.Objectmodeling by registration of multiple range images［C］//The 1991 IEEE International Conference on Robotics and Automation，Sacramento，CA，USA，1991：2724-2729.

［3］Wang Sen，Wang Yang，Jin Miao，etal.Conformalgeometry and its applications on 3D shapematching，recognition，and stitching［J］.Medical Engineering&Physics，2007，29（7）：1209-1220.

［4］ÅströmK，Karlsson J，EnquistO，etal.Automatic feature point correspondences and shape analysiswithmissing data and outliers using MDL［J］.Image Analysis，2007，4522（5）：21-30.

［5］戴静兰，陈志杨，叶修梓.ICP算法在点云配准中的应用［J］.中国图像图形学报，2007，12（3）：517-521.DAIJinglan，CHEN Zhiyang，YE Xiuzi.The Application of ICP Algorithm in Point Cloud Registration［J］.Journal of Image and Graphics，2007，12（3）：517-521.

［6］Yang Shen，Shen Xukun，QiYue，etal.An automated registration method for range images［C］//Proceedings of the 2ndInternationalConferenceonTechnologiesfor E-Learning and Digital Entertainment.Heidelberg，Berlin，Germany：Springer-Verlag，2007：772-783.

［7］Jiang Jun，Chen Jun，Chen Xinglin.Registration for 3-D point cloud using angular-invariant feature［J］.Neuro Computing，2009，72（16-18）：3839-3844.

［8］RUSU R B，BLODOW N，BEETZM.Fast point feature histograms（FPFH）for 3D registration［C］//IEEE International Conference on Robotics and Automation，May 12-17，2009，Kobe，Japan，2009：3212-3217.

［9］王程东，程筱胜，崔海华，等.SIFT算法在点云配准中的应用［J］.传感器与微系统，2012，31（2）：149-152.WANG Chengdong，CHENG Xiaosheng，CUI Haihua，et al.The Application of SIFTAlgorithm in PointCloud Registration［J］.Transducer and Microsystem Technolodies，2012，31（2）：149-152.

［10］YU H，WANG R，CHEN J，et al.Saliency computation and simplication of point cloud data［C］//Proc.2012 2nd International Conference on Computer Science and Network Technology（ICCSNT 2012）.Changchun，China：IEEEPress，2012：1350-1353.

［11］ZHAO X，WEN MH.Kd-tree based non-uniform simplication of 3D point cloud［C］//Proc.2009 3rd International Conference on Genetic and Evolutionary Computing（ICCSNT 2009）.Guilin，China：IEEE Press，2009：339-342.

［12］Lowe D G.Distinctive image features from scale-invariant key points［J］.International Journal of Computer Vision，2004，60（2）：91-110.

［13］Fischler MA and Bolles R C.Random Sample Consensus：A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography［J］.Communicationsof the ACM，1981，24（6）：381-395.