VDOD：一种基于KD树的分布式离群点检测算法∗

李子茂　骆　庆　刘　晶

（中南民族大学计算机科学学院　武汉　430074）

1　引言

离群点检测是数据管理中的热点问题之一［1］，在许多领域有着广泛的应用，如信用卡诈骗、网络入侵检测等。在早期文献［2］中，离群点被描述为：在一个数据集中，若某个数据点与其他数据点的差距非常大以至于被怀疑是通过其他机制生成的，那么该数据点就被认为是离群点。

目前，绝大多数离群点算法都是针对集中式环境设计的。随着物联网、云计算和社交网络等技术的兴起，数据的种类和规模正在不断地增长和积累，大数据时代到来。集中式算法处理效率有限，在多数情况下不能满足用户的需求。因此，一些学者开始使用分布式算法并行计算离群点，以提高计算效率。

本文提出了一种基于方差的数据划分方法，数据划分过程中建立KD树，通过KD树计算划分后的数据块的K近邻将划分后的数据块均匀地分配到各个计算节点，同时能够很好地保证同一计算点上数据的近邻性。基于该划分算法，提出了一种基于R树的分布式离群点检测算法-VDOD。最后通过使用真实数据集和人工合成数据集进行实验，验证了本文提出的基于方差的数据划分方法和VDOD算法的有效性。

2　相关工作

离群点检测的研究最早始于统计领域［1］，基于统计的离群点检测技术假定被检数据符合某个概率分布模型，凡不符合该分布模型的数据点被视为离群点。自那以后，从事数理统计、机器学习和数据挖掘等领域研究的学者们分别从不同的角度提出了多种离群点检测技术和方法［2］。概括起来，主要的离群点检测技术有：基于统计的方法、基于聚类的方法、基于分类的方法、基于距离［3］、基于密度［4］和基于信息熵的方法等，本文主要针对基于距离的离群点检测方法。

基于距离的离群点最早由Knorr等［5］提出，是一种目前被广泛认可的定义标准。Knorr提出了三个检测 DB（k，r）离群点的算法［6］，分别是：基于索引的（Index-based）算法、嵌套循环（nested loop）算法和基于网格（cell-based）的算法。另外，Angiulli等［7］提出了一个基于k近邻（KNN）度量离群程度的方法。Wu等［8］提出了一种基于抽样的方法来考察被测对象与其近邻的关系，即对每个对象，仅考察对象与一个较小的随机抽样的样本集之间的关系，避免了对整个数据集进行距离计算。还出现了针对特定应用背景的离群点检测算法，文献［9］提出了不确定数据的基于距离的离群点检测算法。

在分布式环境中离群点检测的相关研究主要有文献［10～13］。其中文献［10］所研究的问题与本文相同，但提出的PENL算法采用的是基于数量的数据划分方法，不考虑数据分布情况，对于数据集中任意一个数据点 p，在最坏情况下，必须与其他所有数据点计算距离，才能得到最终结果。因此当数据规模较大时，PENL算法需要大量的网络开销，计算效率不高。与本文研究问题最为接近的工作有文献［11］，对PENL算法进行改进提出了BOD算法，采用基于空间的数据划分。该算法中同一计算节点的数据有很好的近邻性，网络开销也大大降低，但是该算法分配到各个计算节点后数据量不均衡，并行计算效率不佳。另外 He Qing［12～13］等基于MapReduce计算离群点和构建并行KD树检测离群点。

3　问题描述

本文主要研究在分布式环境下，如何并行地计算出数据集内所有的基于距离的离群点。下面形式化地给出基于距离的离群点的定义和介绍分布式框架。表1列出了本文使用的主要符号。

3.1　基于距离的离群点检测

在以下的讨论中，设数据集为 X={x1，x2，…，xi，…，xP}，P 为数据集的大小；xi∈X ，为数据集X 中的数据点，记为 (xi1，xi2，…，xij，…，xid)。每个数据点是一个类型为 A=(A1，A2，…，Ad)的d元组，其中d为数据集维度，Aj为属性，d(xi，xj)为度量数据对象xi，xj∈X的距离函数。其中

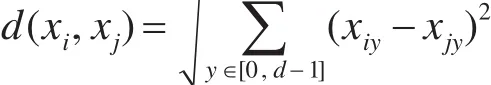
定义1r邻域。对任意实数r≥0，数据对象xi的 r-邻域 Q(xi，r)，定义为

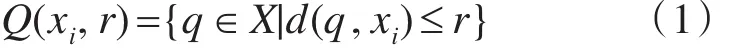
定义2DB(k，r)离群点。给定一个正整数k，如果数据点 x的r邻域的基数小于k，则 x是DB(k，r)离群点。

3.2　分布式框架

分布式环境如图1所示，集群包含固定个数的计算节点 N={n1，n2，…，n|N|}（|N|为节点个数），每个节点都存储数据集X的一个子集，并包含一个查询处理引擎，用于接收查询参数和输出结果，节点之间可以相互通信。

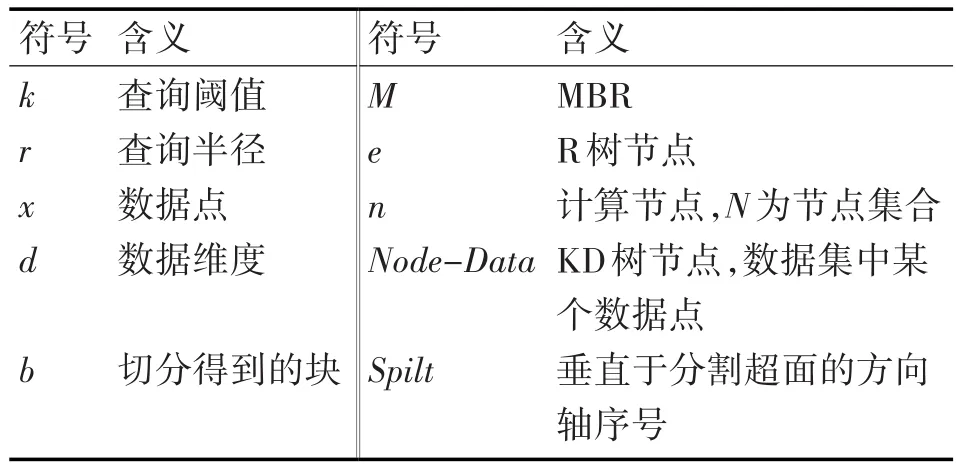
表1　符号表

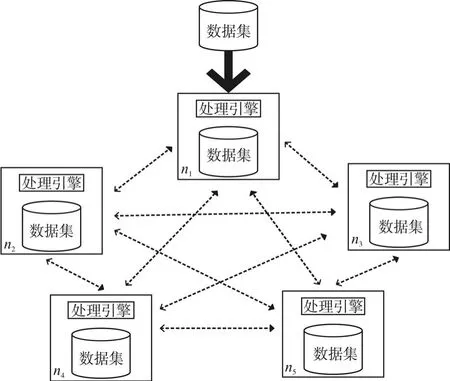
图1　分布式框架

4　数据划分

4.1　块的切分

在介绍划分方法之前，首先介绍下该方法的两个主要输入参数：

1）块（block）：即所需要切分的空间区域。对于d维空间内的一个块b，可以使用块的下界点b.min、上界点b.max表示，记b=［b.min，b.max］。其中对于任意属于块b的数据点满足∀i∈[0，d-1]，b.Min[i]≤ p[i]≤b.max[i]。

2）切分维度。取值范围为［0，d-1］整形变量，用于标识将被切分的维度。

总体上切分算法是一个递归调用的过程。对于一个d维数据块b，需要h次划分将其划分为2h个数据量相等的子块，h满足2h≥N2≥2h-1。划分数据块时从方差最大的第i维的中值点Node-data处进行切分，分成2个数据量相等的子块bleft，bright。其中bleft的下界点bleft.min与b的下界点b.min相同，bleft的上界点的第i维值 bleft.max［i］=Node-data［i］，∀ j∈［0，d-1］且 j≠ I，bleft.max［j］=b.max［j］。相应的 bright.max=b.max，bright.min［i］=Node-data［i］，∀j∈［0，d-1］且 j≠ I，bright.min［j］=b.min［j］。算法1描述了切分的具体过程。

算法1 spilt（block b，dimension D）

1）记切分次数为h，h初始为0；

2）WHILE（2h＜N2）DO；

3）FOR所有子块；

4）计算数据集在0到d-1维上各自的方差，取最大方差维作为spilt；

5）数据点集在第spilt维进行排序，位于中间的那个数据点被选为Node-data；

6）沿着Node-data进行垂直spilt维的切割，计算切割后左右子块的b.min，b.max；

7）END FOR；

8）h=h+1；

9）ENDWHILE。

4.2　块的分配

当切分结束后，最终得到的块的集合表示为B={b1，b2，…，bn}，显然块的数目大于N，需要根据划分时建立的KD树［14］来分配数据块。通过计算各个数据块的几何中心的距离，可以得出数据块的K近邻数据块。每次分配数据块将数据块按照标记进行排序，将第一个数据块和它的p近邻或p-1近邻分配到同一计算节点。重复该过程，直至所有数据块被分配完。

5　VDOD算法

5.1　局部离群点计算

算法首先通过R树［15］结构对数据点进行批量过滤，在本文的计算中，限定每个R树叶子节点包含的数据点的个数的范围为［k，3k］。具体过滤方法如下：

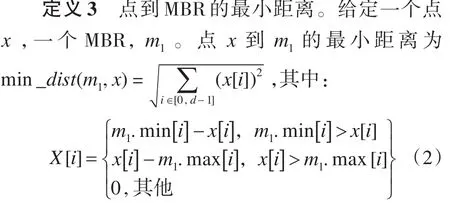
方法一：如果点 x到MBR m1的最小距离Min_dist(m1，x)＞r，则 m1中不存在 x 的近邻点。

方法二：如果已经计算出数据点的近邻点的个数超过k个，那么继续查找它的近邻是没有意义的，因为该数据点已经可以判定为非离群点。

具体过程如算法2所示。

算法2VDOD局部算法

输入：数据集X，考察的近邻个数k，距离阈值r

输出：所有的局部离群点集S，部分全局离群点O

1）初始化堆H为空；

2）nn（p，r）→ 计算 p以r为半径的邻居数目；

3）FOR X中的每一个数据点xi；

4）R树根节点的孩子节点加入到H中；

5）WHILE（H不为空）DO；

6）取H首元素h；

7）IF（Min_dist(xi，h)＞r）DO；

8）h的孩子节点加入到H中；

9）END IF；

10）ELSE；

11）计算h中 xi的近邻点数目nn（xi，r）；

12）IF（nn（ xi，r）≥ k）DO；

13）停止计算离群点，并将xi从X中移除；

14）END IF；

15）ELSE；

16）IF（∀j∈［0，d-1］，xi［j］-b.min［j］≥ r且b.max［j］-xi［j］ ≥ r）DO；

17）将 xi移除到O中；

18）END IF；

19）END ELSE；

20）END ELSE；

21）ENDWHILE；

22）END FOR；

23）X中剩余的数据点为局部离群点集S，输出S、O。

5.2　全局离群点计算

如5.1节所述，如果节点n中存在局部离群点，则节点n需要与其相邻的节点进行网络通信。KD树上的两个数据块，若其中一个数据块的b.min或b.max在另一数据块的空间范围内，则这两个数据块一定相邻。对于节点n的任意块b可求得其它节点上与其相邻的块的集合neig（b）。算法3展示了全局离群点计算的具体过程。

算法3 outlier_judgement（）。

输入：块b中的局部离群点集S，其它节点上与b相邻的块集合neig（b）

输出：S中的全局离群点

1）FOR集合neig（b）中的每一个块 b′DO；2）初始化集合send_（b→b′）；

3）FOR S中的每一个数据点p DO；

4）IFmin_dist（p，b′）≤r THEN；

5） send_（b→b′）→ p；

6） END IF；

7）END FOR；

8）将send_（b→ b′）发送到 b′所在的节点；

9）END FOR。

VOOD算法复杂度分析：算法2的复杂度下界为Ω(d*|X|*log(|X|))，最差情况为O(d*|X|*|X|)。在算法3中，记局部离群点的个数为|S|，每个局部离群点都需要在其它块进行k次查找，则算法4的复杂度下界为Ω(k * d*|S|*log(|S|) ) ，最差情况为O(k*d*|S|*|S|)。

6　实验分析

6.1　真实数据集

本小节主要使用真实数据集来测试VDOD算法性能。试验中使用的集群包括8个计算节点，每个节点的配置为Intel Core i5 2400 3.10GHz CPU，8GB内存，500GB硬盘，操作系统为Red Hat Linux 6.1。算法采用JAVA语言编写，JDK版本为1.8.3，数据集为UCI提供的home sensors for home activity monitoring数据集（链接地址为http：//archive.ics.uci.edu/Ml/datasets），共包括919438条真实数据，每条数据包括5维可度量属性。实验中的对比算法为BOD算法，主要的衡量标准为查询处理时间和通信量（以网络间传输的数据点个数来度量）。表2描述了相关的实验结果。

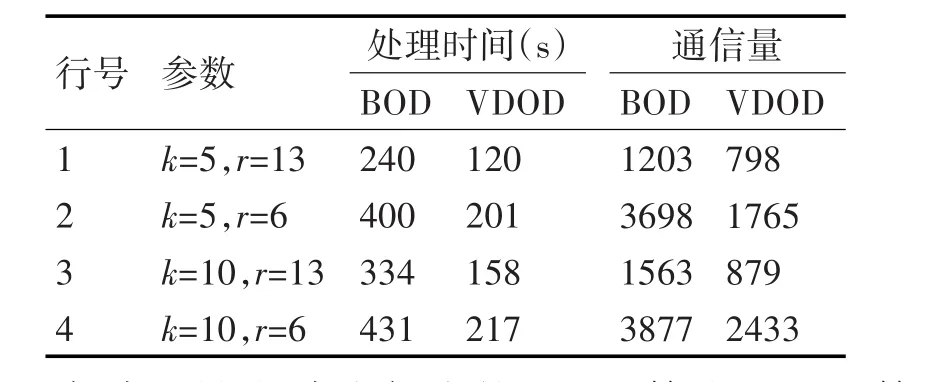
表2　实验结果（真实数据）

如表2所示，本文提出的VDOD算法和BOD算法相比，检测离群点的处理时间和通信量都明显减少。另一方面，通过对表2中1～4行实验结果的比较，容易发现：随着查询半径r的增大，数据集中的离群点表少，BOD和VDOD算法的处理时间和通信量都随之减少；当查询阈值k增大时，离群点变多，导致BOD算法和VDOD算法的处理时间和通信量都增加。

6.2　人工数据集

由于真实数据集规模有限，且无法变化数据维度等参数，因此本小节使用人工合成数据进一步地对算法进行测试。合成数据集为聚簇分布数据，各维的取值范围为0～10000。具体生成方法如下：对于包含a个数据点的数据集，随机生成a/1000聚簇点，每个聚簇内平均包含1000个数据点。在每个聚簇内，数据点以聚簇点为中心呈高斯分布［16］。实验相关变量的默认值和变化范围如表3所示。

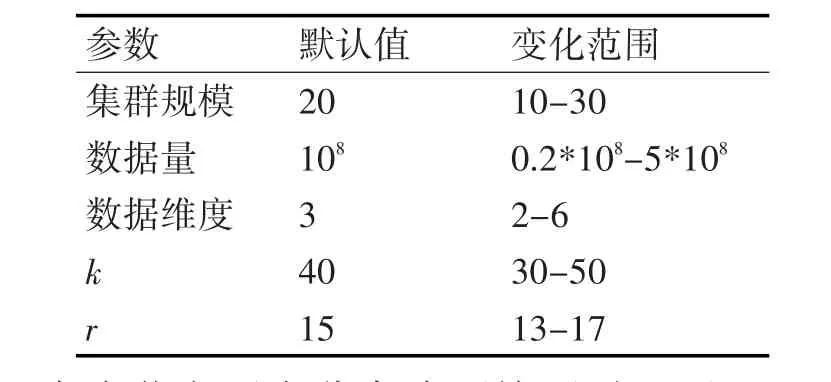
表3　参数设置

本小节主要在分布式环境下对比了VDOD算法与BOD算法的性能。图2描述了集群规模对算法性能的影响。可以看出随着集群规模的扩大，集群的计算能力提高，VDOD和BOD算法的处理时间都随之减少，说明这两种算法都有很好的性能加速比。另外在图3中，节点个数的增加也导致了局部离群点的增多。VDOD算法的通信量轻微增加，而对于BOD算法，更多的节点意味着更多的数据划分，因此网络传输量也随之增加。

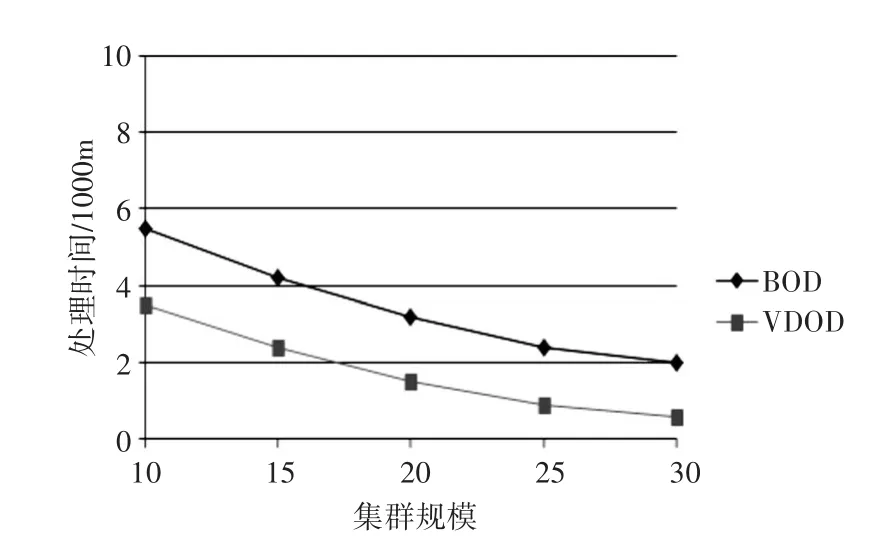
图2　集群规模与处理时间

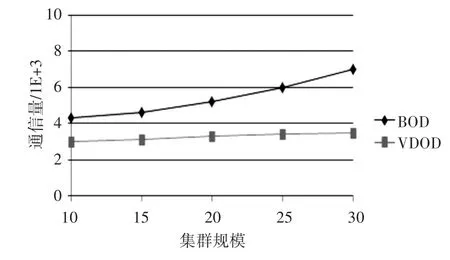
图3　集群规模与通信量

图4、5描述了数据量对算法性能的影响。随着数据量的增加，VDOD和BOD算法都需要消耗更多的系统时间，也会产生更多的网络开销。但通过对比容易发现，VDOD算法的处理时间和网络开销明显低于BOD算法，而且增长速度缓慢。

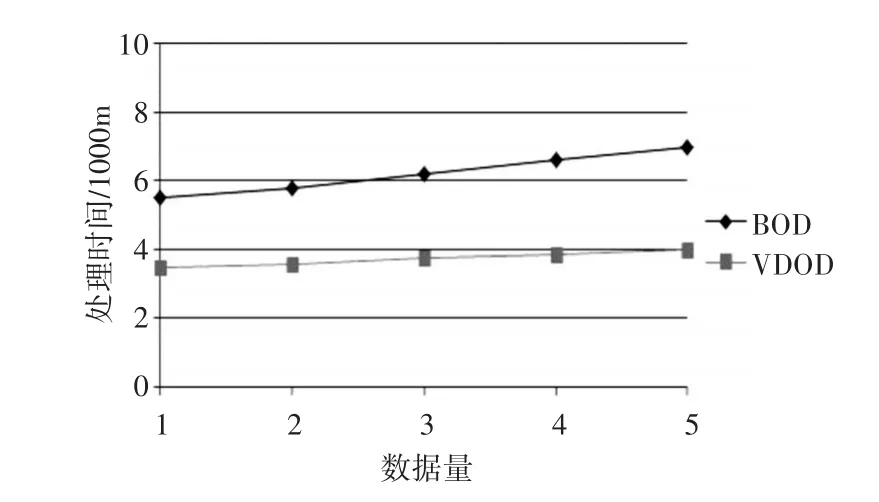
图4　数据量与时间

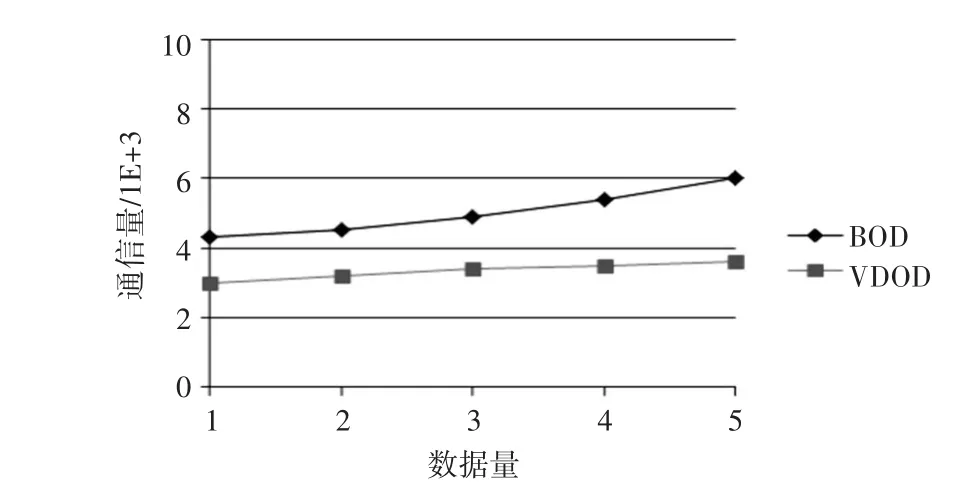
图5　数据量与通信量

7　结语

本文研究了分布式环境下基于距离的离群点检测问题。首先，提出了一种新型的基于方差的数据划分方法，划分过程中建立KD树。该方法对维度不敏感，减少了对数据近邻性的破坏，同时数据基本上实现了均匀分配，提高了并行计算的效率。基于划分方法，提出了VDOD离群点计算算法，该算法包括两个步骤：在每个计算节点本地，基于R树索引进行批量过滤，剪枝掉了大部分的不必要计算，最终快速地计算出局部离群点；进一步地，利用KD树快速确定需要通信的相邻块，并计算输出最终结果。最后通过大量的实验说明了本文提出的VDOD算法的正确性和有效性。

［1］XUEAnrong，JU Shiguang，HEWeihua，etal.Study on algorithms for local outlier detections［J］.Chiness Journal of Computer，2007，20（8）：1455-1463.

［2］ Hawkins D-M，Identification of Outlier［M］.Londin：Chapman and Hall，1980：1-28.

［3］杨茂林.离群检测算法研究［D］.武汉：华中科技大学，2012：1-119.YANG Maolin.Research on Algorithms for Outlier Detection［D］.Wuhan：Huazhong University of Science and Technology，2012：1-119.

［4］Lozano E，Acufia E.Parallel.algorithms for distancebased and density-based outlier［C］//Proceedings of the 15th IEEE international Conference on DataMining.Houston，USA，2005：729-732.

［5］Knorr E-M，Ng R-T.Algorithms for mining distancebased outlier in large datasets［C］//Proceeding of 24th Internatioanal Conference on Very Large Data Bases.New York，USA，1998：392-403.

［6］Knorr E-M，Ng R-T，Tucakov V.Distance-based outliers：algorithms and applications［J］.The VLDB Journal，2000，8（3-4）：237-253.

［7］Angiulli F，Basta S，Lodi S，etal.Distributed strategies for mining outliers in large data sets［J］.IEEE Transactions on Knowledge and Data Engineering，2013，25，25（7）：1520-1532.

［8］Bay S-D，Schwabacher M.Mining distance-based outlier in near linear time with randomization and a simple pruning rule［C］//Proceeding of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Washington，USA，2003：29-38.

［9］Cao K Y，Wang G R，Han D H，et al.Continuous outlier monitoring on uncertain data streams［J］.Journal of Computer Science and Technology，2014，29（3）：436-448.

［10］Hung E，Cheung D-W.Parallel mining of outliers in large database.Distributed and Parallel DataBase［J］.Department of Computer Science and Information Systems，2002，12（1）：5-26.

［11］王习特，申德荣，白梅，等.BOD：一种高效的分布式离群点检测算法［J］.计算机学报，2016，39（1）：36-51.WANG Xite，SHEN Derong，BAIMei，etal.BOD：An Efficient Algorithm for Distributed Outlier Detection［J］.Chinese JournalofComputer，2016，39（1）：36-51.

［12］Koufakou A，Secretan Secretan J，Reeder L，et al.Fast parallel outlier detection for categorical datasets using MapReduce［C］//Proceeding of the IEEE International Joint Conference on Neural Networks.Hong Kong，China，2008：3298-3304.

［13］He Qing，Ma Yun-Long，Wang Qun，et al.Parallel outlier detection using KD-tree based on MapReduce［C］//Proceedings of the 3rd International Conference on Cloud Computing Technology and science.Athens，Greece，2011：75-80.

［14］范文山，王斌.启发式探查最佳分割平面的快速KD-Tree构建方法［J］.计算机学报，2009，32（2）：185-192.FAN Wenshan，WANG Bin，A Fast KD-Tree Construction Method by Probing the Optimal Splitting Plane Heuristically［J］.Chinese Journal of Computer，2009，32（2）：185-192.

［15］胡昱璞，牛保宁.动态确定K值聚类算法的R-树空间索引构建［J］.计算机科学与探索，2016，10（2）：173-181.HU Yupu，NIU Baoning.R-tree Spatial Index Construction Based on Dynamical K-value Clustering Algorithm［J］.Journalof Frontiers of Computer Scicence and Technology，2016，10（2）：173-181.

［16］WANG Xite，SHEN Derong，NIE Tiezheng，etal.An Efficient Algorithmfor Distributed Outlier Detection in Large Multi-Dimensional Datasets［J］.Journal of Computer Science and Technology，2015，30（6）：1233-1248.